GNSS基准站网数据处理方法及应用技巧

多系统数据融合处理原理相较于单系统数据处理更加复杂。首先，它不仅要统一时间和坐标系统，还需要顾及不同系统之间、不同频率观测值之间的偏差等问题。其次，在双频情况下，有些参数无法区分，不得不和其他参数进行合并。当然，处理三频数据时，部分参数是可以分离的，如伪距差分码偏差(DCB)等。为了更为完整地表达GNSS数据处理原理，可将公式(3-8)扩展为：

式(3-51)是基于无电离层组合观测值的一般观测方程，适合多系统多频率GNSS数据处理的数据。观测方程涉及的参数种类多，在实际数据处理中，需要根据实际情况对估计的参数进行一些调整。式(3-8)即是式(3-51)的一种特殊情况。为了推导和描述简便，假设与相位和伪距相关的偏差如u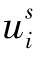ir，，hir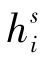，在一段时间内稳定，即假设这些偏差在一天内能作为常数进行估计。

1.单系统双频数据处理

当处理单GNSS系统双频数据时，只能形成一组载波相位和伪距无电离层组合观测值，即i＝1。此时只有一个系统，无需估计系统间偏差Bsys。由于只有一个无电离层组合伪距观测值，接收机和卫星相关的伪距延迟hir和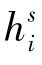无法与接收机和卫星钟差分离，它们将被钟差完全吸收。为了保证相位和伪距钟差定义一致，伪距的相关延迟hir和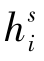也将随着钟差引入相位观测值中，而且接收机相关的和卫星相关的相位延迟(uir和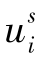)无法与模糊度参数Nci分离，因此需要将这五个参数合并作为一个模糊度参数进行估计。具体观测方程为：

Bci即为合并后的模糊度参数，这与式(3-8)中的bc一致。若将轨道和卫星钟差固定，即为基于无电离层组合观测值的PPP定位模型，而uir＋hir即为接收机端的UPD，即为卫星端的UPD。估计时仅能估计不足一周的小数部分，整数周的部分可以并入模糊度参数，不影响模糊度固定。

2.单系统多频率数据处理

当处理单系统多个频率数据时，即i＞1。此时系统间偏差Bsys仍无需估计。由于存在i组伪距的相关延迟hir和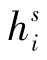，为了保证法方程正常求逆，需要选取一组作为参考，即可估计i-1组伪距相关的硬件延迟。此时在相位观测方程中，同样为了保证钟差定义一致，引入了参考伪距的相关延迟。类似地，需要将相关的模糊度、相位延迟以及钟差引入的伪距延迟进行参数合并。假设将第一个观测值的伪距相关延迟作为基准，则观测方程可以表示为：(www.xing528.com)

类似地，相位观测中的模糊度参数可以与其他四个参数进行合并，作为一个模糊度参数进行估计。从式(3-53)可以看出当处理单系统多频率数据时，只需要选择其中一个伪距相关的延迟作为基准，其他的均需要当成参数进行估计，当然估计得到的值均相对于所选基准。

3.多系统多频率数据处理

当处理多个系统多个频率数据的时候，观测方程与式(3-53)类似，但是对于每个不同的系统，由于选择的伪距相关延迟基准不一样，导致不同系统下接收机钟差定义有矛盾。这就导致了在多系统情况下需要对每一接收机增加一个系统间偏差。其观测方程可以表达为：

其中系统间的偏差Bsys主要是保证两个系统下的接收机钟差定义一致，从式(3-54)中可以推导出系统偏差至少包含着两个系统选择的接收机相关伪距延迟的基准之差system1{h1r}-system2{h1r}。值得指出的是，对于GLONASS这种采用频分多址技术(FDMA)的系统，还需要估计频率间的偏差。假设每一颗卫星的频率均不一致，则需要在每个接收机上对每一颗卫星估计一个频率偏差参数。