现有参数估计方法评述-GNSS基准站网数据处理方法与应用

在GNSS精密定位定轨中，在给出观测值的数学模型后，应使用参数估计方法求出测站坐标等待估参数的最优估值。目前参数估计方法主要包括滤波算法和最小二乘估计算法。

1.最小二乘估计方法

最小二乘估计方法是大地测量中基本的数学工具，也是GNSS精密定位定轨的基本工具。在GNSS基准站网数据处理中，待估参数通常包括测站三维坐标、整周模糊度参数、接收机钟差、ZTD参数等。最小二乘进行参数估计时，首先形成观测方程：

其中，f(x)是包含有待估参数的观测量函数，l为观测值，v为观测误差。将式(3-44)线性化后可得到下式：

式中，A为系数矩阵，由观测方程对待估参数的偏导数组成，即所谓设计矩阵；f(x0)是由待估参数的先验值x0计算得到的理论观测值，v为拟合后的观测残差，dx是待估参数相对于先验值的改正数。

若矩阵A非奇异，即A阵可逆，则可以得到待估参数的最小二乘估值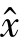。根据最小二乘原理，加权残差平方和vTPv＝min求得唯一解，其中P阵为权矩阵。通过形成法方程并求其逆，可以得到最小二乘解如下：

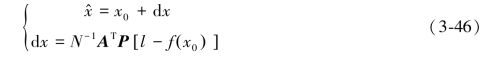
其中，N＝ATPA。

对于基准站网的数据处理来说，观测方程并不对所有待估参数均敏感，例如，双差观测方程中并不包含原点信息，只能估计测站间的相对位置。在这种情况下，若对所有可能的待估参数组成法方程，矩阵N将奇异。为了解决这一问题，通常至少固定一个测站的坐标，对待估参数施加先验约束。此时，最小二乘准则变为vTPvvv＋dxTPxxdx＝min并求得唯一解，其中Pvv是先验参数的权矩阵。对应的，此时最小二乘解为：

待估参数的方差—协方差矩阵为法方程矩阵N的逆矩阵，即

若待估参数已施加先验约束，则为：

其中，为单位权方差，可按下式得到：(www.xing528.com)

r为自由度，即观测数与待估参数个数之差。对于施加了先验约束的最小二乘估计，应将被约束的参数条件也作为观测数(魏子卿等，1998)。

2.均方根信息滤波

滤波算法一般用以解决包含了状态参数的估计问题，能实时输出状态参数及其方差，占用计算机内存资源较少。滤波算法中的卡尔曼滤波(Kalman Filter)(Kalman，1960；Kalman，et al.，1961；Welch，et al.，1995)在众多领域中得到了广泛的应用，并出现了多种变体(Julier，et al.，1997；Wan，et al.，2000)。在GNSS精密定轨定位中，均方根信息滤波(Square-Root Information Filter，简称SRIF)算法(Bierman，1975；Bierman，1982；J.K.Miller，1994；Psiaki，1998)已在美国喷气动力实验室(JPL)研发的高精度GNSS精密数据处理软件GIPSY(Gregorius，et al.，1996；Webb，1993)中得到应用，在处理观测数据时能够有效避免滤波发散，具有较高的数值稳健性和有效性。

3.参数估计方法比较与分析

对于GNSS基准站网的数据处理来说，虽然在解决动态参数估计的问题上滤波算法(特别是均方根信息滤波)具有很大的优势，但GNSS事后精密定位所关心的待估参数多为固定偏差(如测站坐标)，一般不关心中间过程不确定因素影响的状态参数(如接收机钟差、对流层延迟参数、太阳光压参数等)求解。即使需要显式求解状态参数的估值，滤波方法也需要进行进一步的平滑(SRIS)。同时，滤波算法是逐历元求解法方程，SRIF则需要逐历元进行信息矩阵的更新。在大规模基准站网的数据处理中，当测站超过100个时，每历元进行一次法方程求解或信息矩阵更新，将耗费大量的计算时间，特别是当采样间隔较短时，计算时间将呈倍数增长。在GIPSY软件中，为了提高计算效率，将观测数据的采样间隔压缩为每300s一个历元(LICHTEN，1990；葛茂荣，1995)。

为了量化比较不同参数估计方法的效率，我们利用SRIF算法进行参数估计，并采用2009年5月2日的IGS跟踪站网数据(采样率为300s)，分别在50站、100站、150站和200站的数目情况下进行解算。各种情况的测站分布如图3-19所示，得到每历元SRIF解算所花费的时间如图3-20所示，计算机软、硬件平台信息见表3-11。

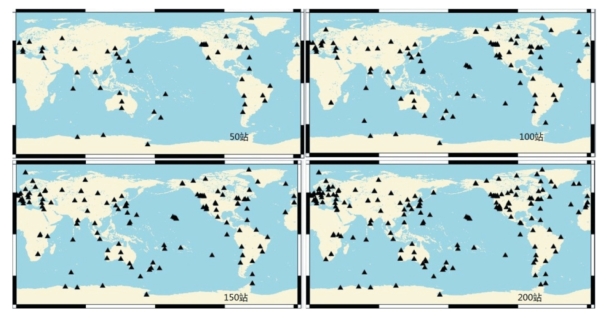
图3-19　SRIF单历元解算测站分布图

表3-11　计算机软、硬件平台

由图3-20可知，随着测站数目的增加，SRIF算法单历元解算时间增长非常迅速。当测站数目为150个时，单历元解算时间超过5min；而测站数目为200个时，单历元解算时间超过了15min，由此推断，解算采样率为300s的全天观测数据时间将超过72h。这对于大规模基准站网数据解算来说，是难以容忍的效率。

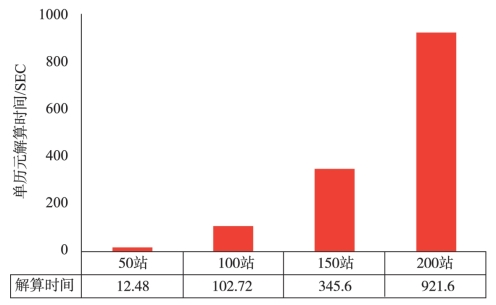
图3-20　SRIF单历元解算时间对比图(单位：秒)

另外，由于最小二乘估计算法不需要逐历元求解法方程，只需在观测时段的每个历元进行法方程叠加，直到最后一个历元才显式求解GNSS精密定位所关心的确定性参数和状态参数，因此在计算效率上具有优势。同时，如果将状态方程和状态参数的先验信息转化为伪观测值并参与法方程叠加，那么最小二乘估计算法与卡尔曼滤波算法是等价的(崔希璋等，2001)。

因此，对于大规模基准站网的事后静态数据处理，采用最小二乘算法进行高性能参数估计可能更为合适。