GNSS基准站网数据处理方法及影响-考虑主要因素

在高精度GNSS数据处理中，影响解算结果精度的主要因素有：卫星星历、地面起算点坐标误差、地面基准与星历框架/历元统一时归算方案的不同、基线解算方案与软件的不同、对流层折射的修正精度、周跳的修复与整周模糊度的固定等(姜卫平等，2001)。本节主要针对这些因素作一些具体分析。

1.卫星星历

(1)卫星星历基准变化引起的系统误差

在GNSS相对定位中，一般采用双差模型，基线Δbij可表示为：

式中，i、j表示测站号，xi为已知点坐标，Aij、lij分别为双差观测方程的系数矩阵、常数项，P为权阵；

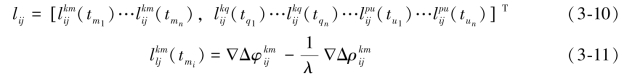
式中，∇Δ表示“双差算子”，k、m、q、p、u代表卫星号，i、j代表测站号。由于卫星星历系统不同带来的自由项的变化可表示为：

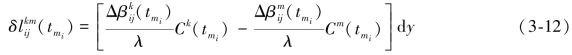
式中，或表示tmi时刻测站i和测站j至卫星k或m的方向余弦差。

即

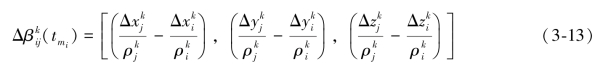
而

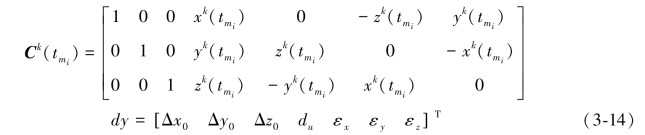
式中，xk(tmi)、yk(tmi)、zk(tmi)分别表示tmi时刻卫星k在精密星历所参照的坐标参考框架下的坐标，dy表示精密星历所参照的坐标参考框架至测站所参照的坐标参考框架之间的转换参数(3个平移参数，1个尺度因子，3个旋转参数)；

不同的精密星历所参照的地球坐标参考框架略有差异。框架之间坐标原点的平移差异为0.05～0.50m，尺度差异为0～0.05×10-6，坐标定向差异为0.01～0.02"。坐标参考框架的变化对GPS基线向量单个分量的影响，其影响数值在最不利的情况下的影响量见表3-1(施闯等，1999)。

表3-1　坐标参考框架系统的变化量对基线分量的影响

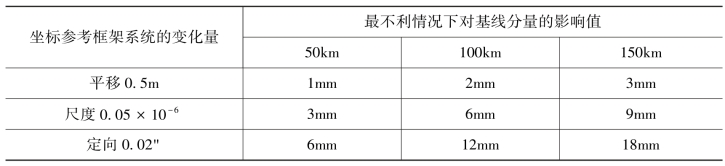
表3-1中三种因素对GPS基线向量各分量的综合影响最大可达到1.36×10-7，一般情况下为5×10-8左右。这样对于不同期的GPS监测网，由于采用的星历不同，会给基线带来较大的误差，并且这一系统误差是不容忽视的。

(2)星历误差

1984年Bauersima给出了卫星轨道误差dr与其对基线影响db之间的关系，参见式(3-1)。但从统计学的角度来讲，轨道误差对基线的影响可以较精确地用式(3-15)表示：

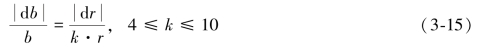
式中，b为基线长度，r为测站到卫星的平均距离，db、dr分别为基线、星历误差。

由此式可得在最不利的情况下其对不同长度基线的影响见表3-2所示。

表3-2　星历误差对不同长度基线的影响

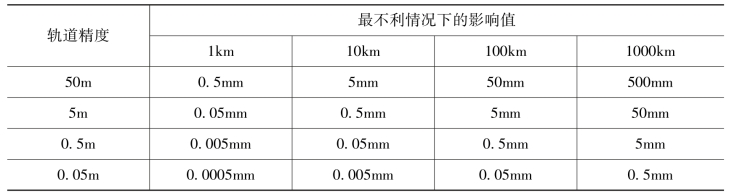
早期的精密星历精度为几米乃至几十米，而最新的IGS事后精密星历精度可达2cm，广播星历的精度一般在10m左右。在解算基线时，应根据网尺度的大小、基线的长短来决定采用哪种星历。从表3-2可以看出，如以0.5mm为限，广播星历(10m)只能满足5km以下基线的精密定位。因此对于5km以上的基线，数据处理时应采用精密星历。此外，不同时期的星历和不同机构发布的星历，也存在着一定的系统性误差。处理时，应尽可能采用同一种类型的星历。特别地，如果所用的精密星历不能满足需要，如1993年以前所测的数据(由于NGS、CODE、SIO等所用的精密星历精度只有2m左右)，在处理时必须顾及星历误差对基线的影响，在定位时，应采取强约束高精度地面基准站坐标并同时松弛轨道的方案(刘经南等，1998)。

2.地面起始点坐标所引起的系统误差

在基线解算中，需要一个起算点，起算点的精度将影响基线解算的精度(姜卫平等，1998)。当基准起算点坐标出现误差时，将导致整个GPS形变监测网基线向量解的系统性误差。研究表明这种系统误差主要反映为整网基线向量的系统性旋转和尺度的变化，式(3-15)可较为准确地用来表征基线起算点误差对基线尺度和方向误差的影响，此时，该式中的dr代表起算点某一方向的坐标误差。当dr是高程误差时，将主要引起网的尺度系统误差。

起算点对基线解算的最大影响可以用下式表示(周忠谟，1997)：

式中，ds为对基线的影响，b为基线的长度，dx为起算坐标的误差。根据此式，在最不利情况下，基准站坐标对基线的影响可以用表3-3表示。

表3-3　基准站坐标误差对基线的影响

续表(www.xing528.com)

由表3-3可知，如以基准站坐标误差对基线的影响量0.5mm为限，基线处理时应注意如下三点：

①对于短基线(＜10km)，其基准站坐标精度应优于1m；

②对于中长基线(＜100km)，其基准站坐标精度应优于0.1m；

③对于长基线(＞100km)，其基准站坐标精度应优于0.05m。

因此，应根据实际情况，通过与连续跟踪站或高等级控制点联测，获得基准站的坐标。对于整个GNSS网，在进行基线解算时，应采用一个或一组测站的坐标，作为固定或松弛的坐标基准；并应先从有已知基准站的同步观测网开始解算，然后用推算得到的未知测站的坐标作为基准来解算相邻的同步观测网，乃至整个GNSS网。

3.地面基准与星历的框架、历元统一时不同归算方案引起的误差

GNSS相对定位的基准是由卫星星历和基准站坐标共同给出的，并且要求地面基准站坐标的框架及历元与卫星星历的框架及历元保持一致性。因此，为了确定在严格基准下的基准站地心坐标，要将GNSS网纳入到ITRF参考框架中，即在处理时应加上在ITRF参考框架中已知坐标的基准站数据一起处理，并应统一地面基准站坐标与卫星星历的框架及历元。

统一地面站坐标与星历的框架及历元有两种方法：一种方法是将星历的框架和历元保持不动，而将地面站坐标的框架及历元归算到星历所在的框架和历元；另一种方法是将星历框架归算至地面站框架而历元保持不动，对地面站只归算历元，而框架保持不动，从而保证框架和历元的一致性。这两种方案的差异对基线精度要求为10-9量级的结果的影响可以忽略不计。

4.基线解算方案和软件不同引起的系统误差

(1)基线解算方案不同引起的系统误差

处理解算的方案不一致，即使所用的软件一致，也会带来较大的系统误差。如电离层和对流层改正模型的选取方式、基准站坐标和卫星轨道的固定或松驰约束程度、力模型的选择、周跳修复的方法，等等，这些因素的影响将造成基线解在尺度和方向上的系统误差。

利用项目“中国地壳形变运动与监测”GPS监测网中的连续三天共三个时段观测数据，采用如下三种方案对此问题进行了研究：

方案一：使用并强约束全球站(十五个)，松弛IGS轨道；

方案二：不使用全球站只固定GM14，并固定轨道；

方案三：不使用全球站只固定GM14，并松弛轨道。

从表3-4中可以看出，不同的解算方案将给监测网中基线向量带来1.5×10-8尺度方面的系统误差。

表3-4　不同解算方案之间基线重复性比较

为了避免不同解算方案对基线所带来的系统误差，对于不同期的数据应严格采用同一方案进行处理。采用的解算方案应特别注意网的尺度、基准站坐标和星历的精度。根据大量的数据处理研究，得出了如下削弱系统误差影响的原则：

①对于大规模高精度GNSS网应采用高精度基准站并强约束其坐标和松弛轨道的方案。其约束量应根据先验精度来确定，既不应太紧，也不应太松；

②对于小尺度、高精度GNSS网，应采用强约束高精度基准站固度轨道的方案；

③基准站和星历的约束量大小是否合适可用平差结果的改正数来判断，其判断标准是：基准站和星历的改正数应不大于2倍(或3倍)的约束量。

(2)基线解算软件的差异

即使基线解算时都采用高精度解算软件，如GAMIT、BERNESE等，但不同的基线解算软件，由于其采用的模型、数据处理方式等因素的不同，可能造成基线解算结果的系统性差异。因此，不同期的观测网应采用同一基线解算软件进行处理。

5.对流层折射对精密基线解算的影响

由于对流层中的物质分布在时间和空间上具有较大的随机性，使得对流层折射延迟亦具有较大的随机性，因此，即使在经过模型改正后，由于改正模型精度并不是很高(其中湿分量的改正精度只有80%)，其不能模型化的残余偏差依旧是影响GPS高程精度的主要因素之一，这种影响在精密定位中必须加以顾及。目前，在模型改正的基础上，随机过程方法是最理想的对流层折射模拟方法(邵占英，et al.，1998)，可以达到水蒸气辐射仪的观测精度，显著提高垂直方向上的重复性。

分段线性方法是随机过程的简化(R.W.King，et al.，2010)，它包含了目前使用的单参数方法和多参数方法。从理论上讲，参数越多，便可以更精确地模拟对流层折射的影响，然而随着参数的增多，整个解的强度会随之降低，并且过多的附加参数还可导致法方程的病态甚至秩亏。但是，参数估计得不够，则不足以反映出对流层特别是湿分量部分随时间变化的特征，从而得不出很高的精度。因此，“窗口”的选择(即选择适当的参数，决定每隔多少时间间隔附加一个参数)是分段线性方法的关键。

通过研究发现，每个测站每2小时(或4小时)取一个参数较好，既能反映对流层折射影响的随机性，又能提高解的精度(邵占英等，1998)。选择时间“窗口”的一般原则为：

①在分段线性方法中，取多个参数比取一个参数的基线分量的重复性要好，特别是垂直方向上改善较大(对东西方向也有一定的提高，对南北方向几乎没有改善)，可提高2～3倍。

②对于中等长度基线够成的GPS网(观测时间大于8小时)，每个测站每4小时(或2小时)取一个参数较好，它能较好地反映出对流层折射影响随时间变化的趋势，从而提高基线解的精度。

不同方案之间，大多数基线在尺度上呈现出系统上的差异(缩短或伸长)，这说明了对流层折射残余偏差对GPS网的确有尺度上的影响，并主要体现尺度误差的比例部分上。对于中等长度基线(100～300km)所构成的GPS网来说，其影响为0.5～1.5mm。

6.周跳的修复与整周模糊度确定

周跳是否修复是影响基线解算精度的重要因素之一。特别是在长距离定位中，模糊度的整数特性受大气改正不完善等因素的影响而变得很弱，周跳是否修复的问题尤为突出。修复周跳的方法有多种，如利用观测值的不同差分(或组合)、拟合法等。

当以相位观测值为观测量进行相对定位时，整周未知数的确定是一个关键问题，其解算的质量如何是相对定位精度的保障。解算整周未知数的方法有多种，如交换天线法、P码双频技术、滤波法、搜索法和模糊度函数法等。整周未知数的结果有两种：整数解和实数解。关于GNSS网解算过程中的整周模糊度问题，将在本书的第4章进行详细论述。