卫星误差的处理与应用方法

1.卫星轨道误差

卫星星历表示的卫星轨道与真实的卫星位置之间的不符值称为卫星轨道误差，其大小取决于轨道计算的数学模型、软件，采用的是跟踪网规模、分布及数据观测时间的长短。相对定位中，轨道误差的影响可按式(3-1)估算。

式中，r是测站到卫星的平均距离；b是基线长度，db、dr分别为基线、星历误差。取r＝20200km，采用IGS提供的精密预报星历(其精度为5cm)，对于50km的基线的最大影响为：

2.卫星钟差改正

卫星钟差是指由于卫星钟频率漂移引起的GNSS卫星时间与标准时之间的差值。广播星历卫星钟差的精度在5～10ns。在相对定位模式下，卫星钟差可通过测站间差分消除。对于非差定位则应该事先估计其大小，然后代入观测方程以消除该项误差的影响。若要实现厘米级精度的精密单点定位，就要求卫星钟差的改正精度达到亚纳秒级。目前，IGS提供的精密钟差产品以5分钟或30秒间隔给出，其RMS为75微秒，STD为20微秒(Larson，et al.，2005)。GNSS观测值的采样间隔一般都小于上述值，此时需内插计算得到每个历元所对应的卫星钟差。内插一般采用低阶多项式就可以满足精度要求。

3.卫星天线相位中心偏差改正

GNSS观测量是相对于卫星天线相位中心的，而卫星定轨所用的轨道力模型参数、IGS精密星历和卫星钟差是相对于卫星质量中心，因此建立观测方程时必须顾及卫星天线质量中心和相位中心之间的偏差。卫星天线相位中心相对于卫星质量中心的偏差一般以星固坐标系中偏差量的形式给出。假定在惯性坐标系中，星固坐标系轴的单位矢量为，，，卫星天线相位中心的位置矢量为，则在惯性坐标系中的卫星天线相位中心偏差可表示为：

已知卫星质量中心的位置矢量为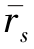，则卫星天线相位中心在惯性系的坐标为：(www.xing528.com)

一般在卫星发射前会测出该偏差量，数据处理时直接进行改正。但是卫星在运行过程中，该偏差由于种种原因可能发生变化，这就会给数据处理带来误差。目前多个GNSS分析中心通过大量的数据处理估计出天线相位偏差，并发布在网上，且自2006年起IGS已采用天线的绝对相位中心改正。

4.相对论延迟

相对论延迟是由于卫星钟和接收机钟所处的状态(运动速度和重力位)不同而引起的卫星钟和接收机钟之间产生相对钟误差的现象。卫星钟比地面钟走得快，每秒约差0.45ns。为了保持地面接收到的信号频率与GNSS导航系统设计的信号频率相一致，在卫星发射之前，人为地将卫星钟的标准频率减少约0.00457Hz。但由于GNSS卫星轨道并非圆轨道，且卫星所在的位置受到的地球重力场影响也不同，相对论效应对卫星钟频率的影响并非一常数，经过上述改正后仍有残差，这部分影响可以用以下公式改正(Kouba，et al.，2001)：

式中，Xs和分别表示卫星的位置和速度向量，c为真空中光速。

5.相位缠绕改正

GNSS卫星发射的是右旋极化(RHCP)的电磁波信号，接收机观测到的相位值依赖于卫星与接收机天线间的方位关系。接收机天线或卫星天线绕极化轴方向的旋转会改变相位观测值，最大可达一周(天线旋转一周)，这个效应就称为“相位缠绕”。对于接收机天线而言，如果是静态观测，天线不发生旋转。但是对于卫星天线，卫星为了保持其太阳能翼板指向太阳，卫星天线相应地会发生缓慢的旋转，而且站星间的几何关系也不断变化。此外，在卫星进出地影区域时，卫星为了使其太阳能翼板指向太阳会快速旋转。卫星在0.5h内可旋转一周，在这段时间，载波相位观测数据需要进行相位缠绕改正，或者删除该部分数据。

在高精度相对定位处理模式下，对于几百千米以内的基线，双差后相位缠绕对定位结果的影响通常可以忽略不计，但对于4000km的基线，其影响量级可达4cm。在固定卫星轨道和卫星钟的载波相位非差精密单点定位中，相位缠绕无法被有效消除，其改正量可达半周，必须加以考虑。