电场强度-大学物理教程

1.静电场

库仑定律仅指出两个点电荷之间的相互作用力的定量关系，并没有说明电荷之间的相互作用是怎样进行的。

电荷间的相互作用是通过电场来实现的，任何电荷都在其周围空间激发电场，电荷间的相互作用可以表示为

1）“场”的特点

场是一种特殊形态的物质，它和物质的另一种形态——实物，一起构成物质世界。

静电场存在于静止点电荷的周围，与实物相比较，其分布范围广泛，具有分散性，所以对场的描述需要逐点进行。

2）电场的基本性质

放入电场的任何带电物体，都会受到电场力的作用。

当带电物体在电场中移动时，电场力对带电物体做功。

2.电场强度

由于电场对处于其中的电荷有作用力，所以可通过观察电荷在空间各点的受力情况研究电场的性质。故引入一个描述电场的基本物理量——电场强度。

下面研究一电荷量为q0的物体周围的电场。电荷量为q0的物体称为场源，场源可以是若干个带电体或点电荷。为了使电场不至于因测量而受到影响，所选用的试探电荷的电荷量和几何线度必须充分小，以保证能反映电场中某一点的性质。对电场中的任何一个场点来说，所受到的电场力的值和方向可能均不同，就某一点而言只与q0的电荷量有关。但力F与q0之比为一个不变的矢量。显然，这个不变的矢量只与该点处的电场有关，反映了电场性质，称为电场强度，简称场强，用符号E表示，即

式（10-2）为电场强度定义式，它表明电场内任意场点的电场强度大小等于位于该点处的单位试验电荷所受的电场力的大小，其方向与正试验电荷在该点受力方向相同。在国际单位制中，电场强度的单位是N·C-1（牛顿每库仑），也可以写成V·m-1（伏特每米）。

3.点电荷的电场强度

设场源为一点电荷，电荷量为Q，在与场源点电荷距离为r的场点处放一电荷量为q0的点电荷，由库仑定律可知，该点电荷受力为

式中，er为由场源点电荷指向场点方向的单位矢量。由式（10-2）可知，该场点的电场强度为

这就是点电荷的电场强度公式。若Q＞0，则E与r同向；若Q＜0，则E与r反向。

4.电场强度的叠加原理

设场源是由n个静止的点电荷q1，q2，…，qn组成的，一个电荷量为q0的点电荷在某一场点P受的合力为

其中，Fi为第i个场源点电荷对点电荷q0的作用力。根据式（10-2），该场点电场强度为

由此可见，由n个点电荷组成的场源在空间某一场点所产生的总电场强度等于各个点电荷单独存在时在该场点所贡献电场强度的矢量和。这就是由静电相互作用的独立性导致的电场强度的可叠加性，称为电场强度的叠加原理。用这个原理，原则上可以计算任意带电体对空间任一场点的场强贡献。如前所述，任意带电体都可无穷分剖为电荷元之集合。

1）点电荷系的场强

设场源由n个点电荷组成，第i个点电荷所带电荷量为Qi，Qi在给定场点P产生的场强为Ei，由式（10-3）有

式中，eri是电荷量为Qi的场源点电荷指向场点P的单位矢量。根据场强的叠加原理，场源在场点P产生的总的场强为

2）电荷连续分布的带电体的场强

对于电荷连续分布的带电体，可把带电体分为许多无限小的电荷元，而每个电荷元都可以当作点电荷，任意电荷元dq在给定场点P产生的场强为

式中，er是电荷元dq指向场点P的单位矢量。根据场强的叠加原理便可求得电荷连续分布的带电体在场点P的场强为

式中积分遍及整个带电体。在这里需要注意，式（10-8b）的积分是矢量函数的叠加积分，在直角坐标系中通常分解为dEx，dEy，dEz三个分量积分式，由此便可求出电场强度矢量的直角坐标三分量。

但是上述叠加积分不能直接进行，除非给出电荷的空间分布函数——电荷密度。

在电荷连续分布的情况下，可以引入电荷密度分布函数，定量地描述电荷的空间分布状况。

若电荷连续分布在细线上（一维），定义电荷线密度λ为

式中，dq为线元dl上的电荷量，λ的单位为C·m-1。由于dq=λdl，所以全部线分布电荷在场点P产生的场强为

若电荷连续分布在一个平面或曲面上（二维），则定义电荷面密度σ为

式中，dq为面积元dS上的电荷量，σ的单位为C·m-2。由于dq=σdS，所以全部面分布电荷在场点P产生的场强为

若电荷在三维空间某区域连续分布，则定义电荷体密度ρ为

式中，dq为体积元dV内的电荷量，ρ的单位为C·m-3。由于dq=ρdV。所以全部体分布电荷在场点P产生的场强为

上面几个公式中，ΔV→0，ΔS→0，Δl→0，并不是严格的数学过程，应理解为宏观无限小，微观无限大的情况。

5.电偶极子的电场强度

两个等量异号点电荷，电荷量分别为+q与-q，相距为r0，如果讨论的场点与这一对点电荷之间的距离比r0大得多，则这一对点电荷的总体就称为电偶极子，用r0表示从负电荷到正电荷的相对位置矢量，电荷量q与r0的乘积叫作电偶极矩或简称为电矩，用p表示，即p=q r0。在国际单位制中，电偶极矩的单位是C·m-1。电偶极子的物理模型是研究介质场和电磁辐射的基础模型。(www.xing528.com)

下面分别讨论电偶极子延长线上和中垂线上任一场点的电场强度。

1）计算电偶极子延长线上任一点A的场强

如图10-2所示。取电偶极子轴线的中点为坐标原点O，沿极轴的延长线为Ox轴，轴上任意点A距原点O距离为x，且x≫r0，由式（10-6）可得电荷+q与-q在点A产生的场强分别为

图10-2　电偶极子延长线上的电场强度

上两式表明，E+和E-的方向都沿着x轴，但指向相反，故A点的合场强EA为

由于r0≪x，故远小于1，于是，于是上式可写为

由于电矩p=q r0=qr0i，所以上式为

2）计算电偶极子中垂线上任一点B的场强

如图10-3所示，设OB=y，且y≫r0，+q和-q在点B所产生的场强大小相等，即

图10-3　电偶极子垂线上的电场强度

总场强为

易知EBy=0，则

当r0≪y时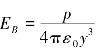，，其方向与电偶极矩方向相反。

例10-1　有一长为L，电荷线密度为λ的均匀细棒。试求：在棒的延长线上，与棒中心距离为a的P点的电场强度。

解　选取坐标如图10-4所示，原点在细棒中心，设棒带正电荷，取任一电荷元dq=λdx，由点电荷电场强度公式得P点的元场强为

图10-4　带电细棒延长线上的电场强度

式中（a-x）为电荷元到场点P的距离，分析知带电细棒上各电荷元在P点电场强度方向一致，由电场强度叠加原理得P点的总场强大小为

上式中，E的方向与x轴平行。

例10-2　如图10-5所示，一个半径为R的细圆环所带电荷量为q，设电荷量均匀分布在环上，且q＞0。求垂直圆环平面的轴线上任意一点的电场强度。

图10-5　带电细圆环中心垂线上的电场强度

解　设坐标原点与环心重合，点P与环心的距离为x，由题意知圆环上的电荷是均匀分布的，故其电荷线密度λ=q/2πR。将细圆环分割为无穷多个带电荷的线元，取其中某一电荷元dl，其上电荷量为dq=λdl，故该电荷元在轴线上任一点P产生的电场强度为dE，则

由于圆环上各个电荷元在P点产生的电场强度的dE⊥上分量相互抵消，因此，P点的电场强度应为全部电荷在P点产生的dEx分量之和，设P点到圆环中心的距离为x，则

式中积分为对整个环求线积分。

再考虑到λ=q/（2πR），cosθ=x/r，。将这些关系代入上述积分可得

（1）显然，当x≫R时，上式化为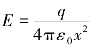，即在远离圆环的地方，带电体系可视为点电荷，这与前面对点电荷的论述相一致。

（2）若x=0，则E=0，这表明环心处的电场强度为零。

（3）由dE/dx=0，可求得电场强度极大位置，故有

这表明，圆环轴线上具有最大电场强度的位置是位于原点O两侧的和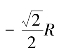处，图10-6是带电圆环轴线上E-x的分布图。

图10-6　带电细圆环轴线上E-x的分布图

例10-3　如图10-7所示，有一半径为R，电荷均匀分布的薄圆盘，其电荷面密度为σ。求通过盘心且垂直盘面的轴线上任意一点处的电场强度。

图10-7　带电薄圆盘中心轴线上的电场强度

解　取如图10-7所示的坐标，薄圆盘的平面在yz平面内，盘心位于坐标原点O，由于圆盘上的电荷分布是均匀的，故圆盘上的电荷为q=σπR2。

把圆盘分成许多细圆环带，其中半径为r，宽度为dr的环带面积为2πrdr，故此环带上的电荷为dq=σ2πrdr，由例10-2可知，环带上的电荷对x轴上点P处激起的电场强度为

由于圆盘上所有带电的环带在点P处的电场强度都沿x轴同一个分向，故由上式可得到圆盘的轴线上P点处的电场强度为

讨论：如果x≪R，带电圆盘可看作是“无限大”的均匀带电平面，这时

于是

上式表明无限大均匀带电平面附近的电场强度E的值是一个常量，其方向与平面垂直，因此，无限大均匀带电平面附近的电场可看成是匀强电场。

此外，若两个相互平行、彼此相隔很近的平面，它们的电荷面密度各为±σ，利用上述结论及电场强度叠加原理，很容易求得两平行带电平面中部的电场强度为E=σ/ε0。