理想气体的等值和绝热过程解析

1.等容过程　摩尔定容热容

在等容过程中，系统体积保持不变。等容过程的基本特点是体积V为常量，即dV=0。等容过程在p-V图上为一条平行于p轴的直线段，即等容线。

系统在准静态过程中状态参量之间的关系式叫作过程方程。理想气体在等容过程中，状态参量既要遵从状态方程，又受到过程特征V为常量的制约，故一定量理想气体等容过程的过程方程为

如图9-3所示，理想气体经过等容过程，由于等容过程dV=0，所以系统做功dW=pdV=0。根据热力学第一定律，过程中的能量关系有

图9-3　等体过程

或

上面各式中的角标V表示体积不变，式（9-5）表明，在等容过程中，外界传给气体的热量全部用来增加气体的内能，系统对外界不做功。

为了计算在等容过程中气体吸收或放出的热量，我们引入摩尔定容热容的概念。

系统在某一无限小过程中吸收热量dQ与温度变化dT的比值称为系统在该过程的热容量，用符号C表示，即

它表示在该过程中，温度升高1 K时系统所吸收的热量，单位是J·K-1。其值由物质和过程决定，对于给定的系统（物质），进行的过程不同，其热容量也不同。若系统物质的量是1mol，则1mol物质的热容量叫摩尔热容（Cm），单位为J·mol-1·K-1。热容量与摩尔热容的关系为，式中m′为物质的质量，M为物质的摩尔质量。

1 mol理想气体，在等容过程中吸收热量dQV与温度的变化dT之比为摩尔定容热容，即。由等容过程知dQV=dE，所以有

对于摩尔定容热容为CV，m，而物质的量为ν的理想气体，在等容过程中，其温度由T1改变为T2时，所吸收的热量为

式（9-7）亦可写成

由式（9-9）可以看出，对给定摩尔定容热容CV，m的1mol理想气体，其内能增量仅与温度的增量有关。因此，1mol给定的理想气体，无论它经历什么样的状态变化过程，只要温度的增量dT相同，其内能的增量dE就是一定的。也就是说，理想气体内能的改变只与起始和终了状态温度的改变有关，与状态变化的过程无关。

由式（9-9）可知，1mol理想气体的内能增量为CV，mdT，因此对于物质的量为ν的理想气体，在微小的等体过程中内能的增量为

已知理想气体的内能为

由此得

把它与式（9-10）相比较，可得

式（9-11）说明，理想气体的摩尔定容热容是一个只与分子的自由度有关的量，它与气体的温度无关。对于单原子理想气体分子，i=3，CV，m=；对于刚性双原子气体i=5，CV，m=；对于刚性多原子气体i=6，CV，m==3R。

2.等压过程摩尔定压热容

在等压过程中，系统的压强保持不变。等压过程的特点是p为常量，即dp=0。等压过程在p-V图上是一条平行于V轴的直线，即等压线，如图9-4所示。理想气体等压过程的过程方程为

图9-4　等压过程

在等压过程中，向气体传递的热量为dQp，气体对外所做的功为pdV，所以热力学第一定律可写为

式（9-13）表明，在等压过程中，理想气体吸收的热量一部分用来增加气体的内能，另一部分使气体对外做功。

对有限的等压过程来说，向气体传递的热量为Qp，则有

得

根据理想气体的状态方程，可得出等压过程中系统对外所做的功为

等压过程中系统对外所做的功在数值上等于等压线下矩形的面积。

为了计算在等压过程中，气体吸收或放出的热量，我们也引入摩尔定压热容的概念。

设有1mol的理想气体，在等压过程中吸收热量dQp，温度升高dT，则气体的摩尔定压热容为

由上式可得在等压过程中，1mol理想气体的温度有微小增量时所吸收的热量为

故摩尔定压热容恒定而物质的量为ν的理想气体在等压过程中吸收的热量为

联立式（9-13）和式（9-15a），得

对于1mol的理想气体，因dE=CV，mdT，及定压过程pdV=RdT，所以有

式（9-16）叫迈耶公式，表示理想气体的摩尔定压热容比摩尔定容热容大一个恒量R。也就是说，在等压过程中，1mol理想气体的温度升高1K时，要比等容过程多吸收8.31 J的热量，用于对外做功。

系统的摩尔定压热容与摩尔定容热容之比，用γ表示，叫作比热容比，工程上称它为绝热指数，即

由于Cp，m＞CV，m，所以γ＞1。

对于理想气体，Cp，m=CV，m+R，且，所以有

式（9-17）说明，理想气体的比热容比，只与分子的自由度有关，而与气体状态无关。根据式（9-17）不难算出：单原子气体的；刚性双原子气体的=1.40；刚性多原子气体的

3.等温过程(www.xing528.com)

系统温度保持不变的过程叫作等温过程，其特征是dT=0，即dE=0。等温过程的过程方程为

在p-V图上，等温过程可用双曲线的一支——等温线来表示，如图9-5所示。

图9-5　等温过程

因为在等温过程中，温度保持不变，而理想气体的内能是温度的单值函数，因此，在等温过程中，内能不变，内能的改变量等于零。即

为了得出等温过程中功的计算式，我们先找出此过程中压强p随体积V变化的关系。由气体状态方程可得

于是等温过程中功的计算式为

根据等温过程的过程方程p2V2=p1V1，上式还可以表示为

根据热力学第一定律及ΔE=0，可得在等温过程中吸收的热量为

式（9-19）表明，在等温过程中理想气体的温度虽然不变，但仍然要与外界交换热量。当理想气体等温膨胀时（V2＞V1），系统吸收的热量全部用来对外做功；当等温压缩理想气体时（V2＜V1），外界对气体所做的功全部转化为系统对外放出的热量。

4.绝热过程

系统不与外界交换热量的过程叫作绝热过程。由绝热材料包围的系统的变化过程，或时间极为短暂，系统来不及与外界交换热量的过程都可近似看成是绝热过程。绝热过程的特点是在任意微小过程中都有dQ=0，于是整个过程中热量Q=0。

当系统由温度T1经绝热过程变为温度T2时，内能的增量仍为

由于在绝热过程中Q=0，根据热力学第一定律可得

这就是说，绝热过程中系统内能的改变，完全取决于系统对外所做的功。当气体膨胀对外做功（W＞0）时，其内能必然会减小（ΔE＜0）。人们常用这一原理获得低温，即让气体绝热膨胀对外做功，使系统的温度下降。反之，当外界对系统做功时，气体内能就会增加，柴油机就是通过迅速压缩汽缸内的气体升高温度，使之达到柴油燃点而爆发做功。

在准静态绝热过程中，理想气体状态参量p、V、T不是独立的，它们之间的关系可由理想气体状态方程和热力学第一定律来求得。对于一个微小的绝热过程，热力学第一定律可表示为

将理想气体状态方程微分，可得

将上述两式联立，消去dT，得

因Cp，m=CV，m+R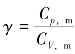，，则有

将上式两边积分，得

或

应用和式（9-21）分别消去p或V可得

根据式（9-21），可在p-V图上画出绝热过程所对应的曲线，叫作绝热线。由于γ=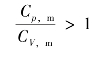，因此过同一点的绝热线要比等温线陡一些，如图9-6所示。

图9-6　绝热线比等温线陡

例9-1　有2mol氦气，由初始状态a（T1，V1）等压加热至体积增大1倍，再经绝热膨胀，使其温度降至初始温度，如图9-7所示。把氦气视为理想气体，试求：（1）整个过程氦气吸收的热量；（2）氦气所做的总功是多少。

图9-7　例9-1图

解　（1）根据状态方程有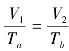，即

各过程吸收的热量为

整个过程吸收的热量

（2）对整个过程应用热力学第一定律，则

依题意，Ta=Tc，故ΔE=0，总功为

例9-2　1mol双原子分子理想气体的p-V关系如图9-8所示，由初态A（p1，V1）经准静态过程直线变到终态B（p2，V2）。试求该理想气体在A→B过程中：（1）内能增量；（2）对外界所做的功；（3）吸收的热量；（4）A→B过程的摩尔热容。

图9-8　例9-2图

解　（1）内能增量为

（2）A→B过程做的功为曲线下梯形的面积，故

因AB为过原点的直线，根据相似三角形有p1V2=p2V1，则

（3）由热力学第一定律，吸收的热量为

（4）根据状态方程，热量可写为

对于A→B过程中，任一微小状态变化均应有

由摩尔热容定义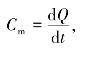得