麦克斯韦速率分布律-大学物理教程

1.麦克斯韦气体分子速率分布律

处于平衡态下的气体分子的运动是杂乱无章的，分子之间频繁的碰撞使得每一个分子运动速度的大小和方向不断变化，各个分子的速度千差万别，不尽相同。这种分子运动的无规律性和偶然性，使得我们不可能详细了解每一个分子的速度状况。但若从大量分子的整体来看，仍有可能找出一些关于分子速率的统计性规律。这个规律在1859年由麦克斯韦采用数学统计方法从理论上导出，我们把理想气体分子速率分布规律叫麦克斯韦气体分子速率分布律（简称麦克斯韦速率分布律）。

分子速率的分布函数为

式中，T是热力学温度；m为分子质量；k为玻尔兹曼常数。式（8-9）适用于平衡态下的理想气体，它是分子质量与气体温度比的函数，其速率分布曲线如图8-3所示。

图8-3　理想气体的速率分布曲线

曲线下面宽度为dv的面积等于分布在此速率区间内的分子数占总分子数的比率。同一种理想气体在平衡态下，温度升高时速率分布曲线变宽、变平坦，但曲线下的总面积不变。随着温度的升高，速率较大的分子在分子总数中的比率增大。同一温度下，分子质量m越小，曲线越宽、越平坦，在分子总数中速率较大的分子所占比率越高。

1）速率分布函数f（v）

是v的函数，在不同速率附近取相等的区间，此比率一般不相等。当速率区间足够小时（宏观小，微观大），还应与区间大小成正比。

因此有

式（8-10）的物理意义为：在速率v附近，速率区间v～v+dv中的分子数占总分子数的比率（分子处于单位速率间隔内的概率）。则dN=Nf（v）dv表示：在速率v附近，速率区间v～v+dv的分子数。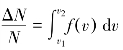表示：在速率v附近，速率区间v1～v2的分子数占总分子数的比率。表示：在速率v附近，速率区间v1～v2的分子数。

2）归一化条件

因速率分布在0～+∞内的分子数是总分子数N，进而有

式（8-11）表示速率0～+∞整个速率范围内的分子数占总分子数的比率为1，这个结论是由速率分布函数的物理意义所决定的，它是速率分布函数所必须满足的条件，叫作速率分布函数f（v）的归一化条件。

2.几个特征速率

1）最概然速率vp

由图8-3可知，速率分布曲线有个高峰，即速率分布函数f（v）有一个极大值。与f（v）极大值对应的速率叫作最概然速率，通常用vp表示。它的物理意义是：在一定温度下，在0～+∞整个速率范围内，vp附近单位速率区间内的分子数占总分子数的概率最大。用求函数极值的方法表示，即

可求得满足麦克斯韦速率分布律的平衡态下气体分子的最概然速率为(www.xing528.com)

所得结果说明，温度越高，vp越大，速率分布曲线的高峰向速率大的一方移动；气体的摩尔质量越大，vp越小，速率分布曲线的高峰向速率小的一方移动。

2）平均速率

为大量分子速率的统计平均值，根据求平均值的定义有

将麦克斯韦速率分布函数f（v）代入，可得理想气体速率从0到+∞整个区间内的算术平均速率为

用来讨论分子的碰撞，计算分子运动的平均距离、平均碰撞次数等。

3）方均根速率

根据平均值公式，速率v的平方的平均值为

将麦克斯韦速率分布函数f（v）代入，可得理想气体分子的方均根速率为

方均根速率用于计算分子的平均平动动能，在讨论气体压强和温度的统计规律中使用。

从以上结果可以看出，气体分子的三种特征速率vp和都与成正比，与或成反比。在这三种速率中，方均根速率最大，平均速率v 次之，最概然速率vp最小。在室温下，它们的数量级一般为每秒几百米。这三种速率对不同的问题，有各自的应用，从不同的方面反映气体分子热运动的规律。

3.麦克斯韦速率分布曲线的性质

当温度升高时，气体分子的速率普遍增大，速率分布曲线中的最概然速率vp向量值增大的方向迁移。但归一化条件要求曲线下总面积不变，因此，分布曲线宽度增大，高度降低，整个曲线变得较平坦，如图8-4所示。

图8-4　不同温度下分子速率分布

在相同温度下，对不同种类的气体，分子质量大的，速率分布曲线中的最概然速率vp向量值减小方向迁移。因总面积不变，所以分布曲线宽度变窄，高度增大，整个曲线比质量小的显得陡些，即曲线随分子质量变大而左移，如图8-5所示。

图8-5　不同质量的分子速率分布