大学物理教程：波的衍射、干涉与驻波的理论解析

本节我们讨论几列波在介质中同时传播并相遇的时候，介质中各质点的运动规律。

1.惠更斯原理

波动的传播是由于介质中质点之间的相互作用，介质中任何一质点的振动将直接引起临近各质点的振动，因此，波动到达的任一质点都可看作新的波源。例如，水面波传播时如果前进中遇到一个有孔的障碍物时，不论之前的波面是什么形状，只要小孔的限度远小于波长，小孔的后面就出现了圆形波，该圆形波好像是以小孔为波源产生的一样，与原来的波的形状无关。这说明小孔可以看作新的波源，其发出的波称为次波（子波）。

在研究这类现象时，1690年荷兰物理学家惠更斯提出，介质中波面上的各点，都可以看作是发射子波的波源，之后任一时刻这些子波的包络面就是新的波面，这就是著名的惠更斯原理。

惠更斯原理对任何波动过程都适用，不论是电磁波还是机械波，也不管传播的介质是否均匀，只要知道某一时刻的波面，就可以根据这一原理采用几何作图的方法确定下一时刻的波面，进而确定波的传播方向。

如图6-9所示，以O为中心的球面波以波速u在介质中传播，在t时刻波面是以R1为半径的球面S1。根据惠更斯原理，S1上的各点都可以看作发射子波的波源。以S1上各点为中心，以r=uΔt为半径画出许多半球面形的子波，这些子波的包络面S2就是形成的新的波面。显然，S2是以O为中心，半径为R2=R1+uΔt的球面。

如果已经知道平面波在某时刻的波面S1，根据惠更斯原理，同样可以求出以后任一时刻新的波面，如图6-9所示。

图6-9　用惠更斯原理求新的波阵面

（a）球面波；（b）平面波

从上述讨论中可知，当波在各向同性均匀介质中传播时，波面的形状总是保持不变，即波的传播方向保持不变。同理，波在各向异性的介质或者非均匀介质中传播时也可以根据惠更斯原理求出新的波面，只是波面的形状和波的传播方向都可能发生变化。

2.波的衍射

波的衍射是指波在传播过程中遇到障碍物时，传播方向发生改变，能绕过障碍物的边缘继续前进的现象。

用惠更斯原理可以说明波的衍射现象。如图6-10所示，当一平面波到达一宽度与波长相近的缝时，缝上的各点都可以看作发射子波的波源，根据惠更斯原理用几何方法可以作出这些子波的包络面，就得出新的波前，此时已不再是平面，波动扩展到了按直线传播应该是阴影的区域，靠近边缘处波面弯曲，波的传播方向发生了改变，表示波已绕过障碍物的边缘而继续传播。

图6-10　波的衍射

衍射现象是否显著，是由障碍物的大小与波长之比决定，比值越小，衍射现象越明显。室内能够听到室外的声音，就是由于声音的波长和所碰到障碍物的大小差不多，声音绕过了门窗。

3.波的叠加

在生活中，我们经常遇到几列波同时传到某一处相遇，分开后仍保持原波特性（频率、波长、振动方向等）继续传播。例如，乐队合成或几个人同时谈话时，人们能分辨出各种乐器或各个人的声音，不同电台发射的无线电波虽在空中相遇过，但传到收音机天线的电波仍是原电台的电波。通过观察和总结，人们发现波所传播的振动不因波相遇而发生相互影响，每个波列都保持单独传播时的动态特性而继续传播，这称为波的独立传播原理。

从波的独立传播原理可以得出结论：波相遇处，介质中各点的振动就是各波列单独传播时在该点各振动的合成，这个结论称为波的叠加原理。

对于各种介质中的机械波或电磁波，当波的振幅不大时，叠加原理都成立。但对于大振幅的波，如强烈的爆炸声波和强激光在介质中传播时，叠加原理就不成立，这时相遇波会有互相影响，对于在真空中传播的电磁波（光波），则叠加原理普遍成立。

4.波的干涉

一般情况下，n列波在空间相遇时，叠加的情况比较复杂。如果两列波频率相同，振动方向相同，相位差恒定，这样的两列波称为相干波，满足这些条件的波源称为相干波源。两列相干波在空间相遇时，有些点振动始终加强，而另一些点振动始终减弱，这种现象称为波的干涉。

以上讨论可知，波的干涉出发点仍然是求相干区域内各质元的同频率同方向的简谐振动的合成。

设S1和S2为相干波源，它们的振动方程分别为

式中，ω为圆频率；A1、A2为两波源的振幅；φ1、φ2分别为两波源的振动初相。设由这两个波源发出的两列波在同一介质中传播相遇，现分析相遇区域内任一点P的振动合成情况。

不考虑介质对波能量的吸收，两列波各自传播到点P时的振动方程分别为

式中，r1和r2分别为S1和S2到点P的距离。如图6-11所示，λ是波长，显然，点P同时参与了两个同方向同频率的简谐振动。

图6-11　波的合成

设合振动方程为

合振动的振幅A和初相由以下两式决定：

由于波的强度和振幅的平方成正比，若用I1、I2和I分别表示两分振动和合振动的强度，则式（6-23）可写为

式（6-24）中点P处两分振动的相位差为

对于给定的点P，波程差r2-r1是一个常量，那么Δφ也是确定的。对于空间中不同的质元，由于波程差r2-r1不同，相位差Δφ也不同，因而各点有不同的振幅和波的强度，从而出现振幅或强度分布不均匀，而又相对稳定的干涉图样。

对于满足

的空间各点，A=A1+A2=Amax，合振幅和强度均有最大值，这些点始终加强，称为干涉相长或干涉加强。

对于满足

的空间各点，合振幅和强度均有最小值，这些点始终减弱，称为干涉相消或干涉减弱。

如果两相干波源的初相相同，那么式（6-25）和式（6-26）可化为

式（6-27）和式（6-28）表明，当两个相干波源同相位时，在两列波的叠加区域内，波程差等于半波长的偶数倍的各点，合振幅和强度最大；波程差等于半波长的奇数倍的各点，合振幅和强度最小。

在其他情况下，合振幅的数值则在最大值和最小值之间。两列不满足相干条件的波相遇叠加称为波的非相干叠加，这时空间任一点合成波的强度等于两列波强度的代数和，即

波的干涉是波动的基本特征之一，只有线性波动的叠加，才可能产生波的干涉。

例6-6　如图6-12所示，波源A、B为相干波源，振幅皆为5 cm，频率为100 Hz，当点A为波峰，点B为波谷时，波速为10 m·s-1，试求点P的干涉结果。

图6-12　例6-6图(www.xing528.com)

解　由图可知，AP=15 m，AB=20 m，则

波源A、B在点P的相位差为

因此得，点P因干涉而静止。

例6-7　已知波源B、C为同一介质中的两个相干波源，相距30 m，如图6-13所示。它们产生相干波的频率为ν=100Hz，波速u=400m·s-1，且振幅都相同，已知点B为波峰时，点C为波谷。求BC连线上因干涉而静止的各点的位置。

图6-13　例6-7图

解　设波源B的振动相位φB=0，依题意波源B、C振动相位相反，则波源C振动初相为φC=π。设点P为BC连线上的任意一点，与波源B、C的距离分别为rB、rC。则在点P

由波源B、C所引起的分振动相位差为

由题意知φC-φB=π，且

要想因干涉而静止，其相位差ΔφP必须满足

化简得

现在分三种情况进行讨论。

（1）若点P在波源B左侧，则rB-rC=-30 m，不满足式（1），故点B左侧不存在因干涉而静止的点。

（2）若点P在波源C右侧，则rB-rC=30m，不满足式（1），故点C右侧不存在因干涉而静止的点。

（3）若点P在波源B、C之间，则rB-rC=2rB-30 m，代入式（1）得

即在与波源B距离rB为1 m，3 m，5 m，7 m，…，29 m的各点因干涉而静止。

5.驻波

1）驻波的产生及特点

驻波是在同一介质中两列振幅、频率、振动方向均相同的相干波，在同一直线上沿相反方向传播叠加时形成的合成波，驻波是一种特殊形式的波的干涉。弦线上各点的振幅不同，有些点始终静止不动，相当于振幅为零，称为波节；有些点振动最强，相当于振幅最大，称为波腹，如图6-14所示。

图6-14　驻波形成示意图

2）驻波方程

设两列振幅、频率和传播速度都相同，初相都为零的相干波在同一介质中分别沿x轴正方向和负方向传播，波函数则为

叠加产生的合振动为

由三角关系式，上式可化为

式（6-29）就是驻波方程，式中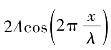与时间t无关，只与位置x有关，相当于振动方程的振幅项，大小随位置x按余弦规律周期性变化。

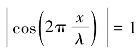在波腹位置处，振幅=2A，即，则

相邻两波腹之间的距离为

在波节位置处，振幅=0，即=0，则

相邻两波节之间的距离为

通过上述分析可知，两相邻波腹和两相邻波节之间的距离都是λ/2，那么可得相邻波腹和相邻波节之间的距离为λ/4，由此可见，只要从实验中测得波节或波腹的距离，就可以确定波长，这也是一种测波长的方法。

下面来讨论驻波的特点。

任选两个相邻波腹的坐标xk=kλ/2和xk+1=（k+1）λ/2，带入式（6-29），则有

式（6-30）和式（6-31）表明两相邻波腹质点的振动相位相反，说明波节两侧的相位相反；式（6-31）中振动系数2A cos kπ根据余弦三角函数的取值变化规律可得，波节两侧有相反的符号，也说明波节两侧的相位相反，那么波节两侧各点同时沿相反方向达到各自位移的最大值，又同时反向通过平衡位置；两波节间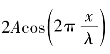具有相同的符号，表明各点的振动相位相同，说明两相邻波节之间各点沿相同方向达到各自的最大值，又同时沿相同方向通过平衡位置。

总之，相邻波节之间（同一段）相位相同，而振幅不同，相邻段相位相反，可见，驻波实质上是一种分段振动的现象。驻波中的各点以确定的振幅在各自的平衡位置附近振动，任一时刻都有一定的波形，波形既不向左也不向右，没有振动状态或相位的传播，没有能量沿某一确定的方向传播，故称之为驻波。换言之，驻波不传播能量，这也是驻波和行波的一个重要区别。

3）半波损失

由入射波和反射波叠加得到的驻波，如固定点处是波节，则入射波和反射波在该固定点的相位是相反的，这表明入射波固定点反射时相位发生了π的相位突变，由于相距半波长的两点相位差为π，因此这种π的相位突变现象称之为半波损失。

一般情况，入射波在两介质的界面上反射时是否有半波损失取决于界面两边的相对波阻。波阻是指介质的密度ρ与波速u的乘积ρu，波阻较大的介质称为波密介质，波阻较小的介质称为波疏介质，当波从波疏介质垂直入射到波密介质界面上反射时，有半波损失，界面处形成波节；当波从波密介质垂直入射到波疏介质界面上反射时，无半波损失，界面处形成波腹。

例6-8　一长弦两端各系在一波源上，所产生的波分别为y1=0.06cos[π（4t+x）]和y2=0.06cos[π（4t-x）]（SI），在弦上沿相反方向传播而形成驻波，求：（1）各波的频率、波长和波速；（2）波腹和波节的位置。

解　（1）将已知波化成平面简谐波的标准形式，则有

与波的标准形式相比较，可得频率为ν=2Hz，波长λ=2m，波速u=4m·s-1。

（2）由得波腹的位置在x=0，±1m，±2m，…；由得波节的位置在x=±0.5m，±1.5m，±2.5m，…。