大学物理教程：波的能量与平均能流的关系

波在弹性介质中传播时，介质中的质元由近及远地振动起来，振动的质元不仅具有动能，而且由于振动质元处介质发生了形变，因而也具有势能。可见，波动的传播伴随着能量的传播，这也是各种波的共同性质。

1.波动能量的传播

我们以在细棒内传播的平面简谐纵波为例导出波动能量的表达式。

如图6-7所示，一密度为ρ，横截面积为S，沿x轴放置的细棒，有一平面简谐纵波以波速u在细棒内沿x轴正方向传播。

图6-7　波在介质中的传播

于棒内任取一体积元dV=Sdx，该体积元的质量为dm=ρdV，当平面简谐纵波

在介质中传播时，体积元在t时刻的振动速度为

那么可得体积元的动能为

该体积元的应变为，当所取体积元无限小时，拉伸应变可写为，即

由弹性模量E的定义及胡克定律，体积元受到的弹力为

则弹性势能可表示为

因为，所以

比较式（6-13）和式（6-14），可见ΔEk=ΔEp，动能和势能在任意时刻都具有相同的表达式，两者的变化是同相位的，同时达到最大值又同时达到最小值；在振动能量中，振动的动能和势能相位不同，动能最大时，势能为零，反之势能最大时，动能为零。可见波动能量和振动能量有着显著不同的特点。

由于体积元的总机械能等于动能和势能之和，可得

从式（6-15）可以得出，体积元的机械能不守恒，而是随时间周期性变化，该体积元不断地从后面的介质中获得能量，又不断地把能量传递给前面的介质，就这样，能量从介质的一端传到了另一端，这说明波动是振动能量的传播。

2.能流和能流密度

波在介质中传播时，介质单位体积内的能量叫波的能量密度，记为w，那么，介质中距振源x处时间t的能量密度为

式（6-16）表明，介质中任一处波的能量密度是关于时间t的函数。通常取一个周期内的平均值，叫作平均能量密度，记作，则有(www.xing528.com)

可见，对于在均匀介质中传播的平面简谐波，各处的平均能量密度均相同。这一结论适用于各种机械波。

波在介质中的传播过程伴随着能量的传播或能量的流动，为了表述波动的传播过程中能量流动的特性，这里我们引入能流和能流密度。

单位时间通过某一面积的能量叫作通过该面积的能流，用P表示。如图6-8所示，设介质中垂直于波速u的面积为S，则dt时间内通过S的能流为

图6-8　通过S的能流

可见，能流也是随时间周期性变化的，取一个周期内的平均值，便有平均能流为

即平均能流的大小和平均能量密度、波速有关，单位为W（瓦）。

垂直通过单位面积的平均能流叫作能流密度（波的强度），记作I，即

能流密度是一个矢量，在各向同性介质中，传播方向与波速相同，矢量表达式为

由式（6-21）可知，对于机械波，能流密度与振幅的平方和圆频率的平方成正比，单位为W·m-2。

实际上波在介质中传播时，能量总有一部分被介质吸收转为热能，因此机械能会不断减少，表现为波的振幅或波的强度沿波传播的方向逐渐减少，这种现象称为波的吸收。在考虑吸收的情况下，波的强度衰减规律为

式中，I0和I分别为x=0和x处波的强度，α取决于介质性质，称为介质的吸收系数。

例6-4　在截面积为S的圆管中，有一列平面简谐波，其波动方程为y=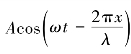，圆管中波的平均能量密度为w，则通过圆管截面的平均能流是多少？

解　根据式（6-19），由于平均能量密度w 和圆管截面积题目已给出，这里只需要计算出波速u的表达式，由于，所以，故

例6-5　用聚焦超声波的方法可以在液体中产生强度为120 kW·cm-2的大振幅超声波。设该超声波的频率为ν=500 kHz，液体的密度为ρ=103kg·m-3，声速为u=1 500m·s-1，求这时液体质元振动的振幅。

解　由可得

可见液体中超声波的振幅实际上是极小的。