大学物理教程，简谐振动合成成果

在实际问题中，一个质点同时参与两个或多个振动（或者某个物理量同时参与两个或多个振动）的现象是经常遇到的。两个或两个以上振动的叠加，称为振动的合成。例如，民乐合奏各种乐器的声音同时引起耳膜的振动，天线接收到多种电磁波而产生的电振动，多束光在空间相遇引起的电场强度和磁感应强度的振动都是振动的叠加和合成问题。一般的振动合成比较复杂，下面讨论四种具有重要意义的特殊情况的简谐振动的合成（叠加）。

1.两个同方向同频率的简谐振动的合成

设一个质点同时参与两个同方向同频率的简谐振动（分振动）：

两个分振动在同一方向进行，那么合位移等于两个位移的代数和，即

由三角函数公式，式（5-25）可化为

式（5-26）中A和φ0分别表示合振动的振幅和初相，且有

由此可以得出，同方向同频率的简谐振动合成后仍为简谐振动，且频率与分振动频率相同，合振动的振幅、相位由两个分振动的振幅A1、A2和初相φ10、φ20决定。

利用旋转矢量法讨论上述问题则更加简洁直观。如图5-15所示，取Ox轴，画出两个分振动的旋转矢量A1和A2，它们与Ox轴的夹角分别为φ10、φ20，以相同的角速度ω沿逆时针方向旋转。由于两个分矢量和的夹角恒定不变，故合矢量的模保持不变，并且以同样的角速度旋转。图中矢量A即t=0时的合振动矢量，任一时刻的位移等于该时刻在Ox轴上的投影，即

可见合振动是振幅为A、初相为φ0的简谐振动，圆频率与两个分振动相同，这和上文的结论一致。

图5-15　同方向同频率的简谐振动的合成的旋转矢量法

现在进一步讨论合振动的振幅和分振动相位差之间的关系，由式（5-27）可知：

（1）当相位差φ20-φ10=±2kπ，k=0，1，2，…时，有

即两个分振动相位相同时，合振幅等于两个分振动振幅之和，且最大。

（2）当相位差φ20-φ10=±（2k+1）π，k=0，1，2，…时，有

即两个分振动相位相反时，合振幅等于两个分振动振幅之差，且最小。

一般情况，两个分振动相位既不相同又非相反时，合振幅在A1+A2与之间。

例5-7　两个同方向同频率的简谐振动分别为x1=4cos（3t）和，x1和x2单位都为m，求合振动方程。

解　两个同方向同频率的简谐振动合成后仍为同频率的简谐振动，设简谐振动的方程为

振幅为

初相为

查表得，φ=0.33。由此得合振动方程为

∗2.两个方向相互垂直的同频率的简谐振动的合成

设一个质点同时参与了两个方向相互垂直的同频率的简谐振动，即

将上两个式子中的t消去，可得到合振动方程为

式（5-28）是椭圆方程，它的形状由相位差Δφ=φ2-φ1决定：

（1）当Δφ=0或者为π的整数倍时，合振动是简谐振动；

（2）当Δφ=时，合成轨迹是正椭圆形状，若A1=A2，则正椭圆形状退化为圆形状；

（3）当0＜Δφ＜π时，质点沿顺时针方向转动；

（4）当-π＜Δφ＜0时，质点沿逆时针方向转动。(https://www.xing528.com)

反过来讲，某个任意方向的简谐振动、某些椭圆运动、某些圆运动也可以分解为两个方向相互垂直的同频率的简谐振动。

由以上讨论可知，两个方向相互垂直的同频率的简谐振动，其合成轨迹可能是直线、椭圆或圆，如图5-16所示。合成轨迹的形态和运动旋转的方向由分振动的振幅和相位差决定。

图5-16　两个方向相互垂直的同频率的简谐振动的合成轨迹

两个方向相互垂直的同频率的简谐振动的合成理论在研究电磁波和光的偏振及偏振实验技术中有重要应用。

∗3.多个同方向同频率的简谐振动的合成

对于一个质点同时参与多个同方向同频率的简谐振动，可以用一个质点参与两个同方向同频率的简谐振动的旋转矢量法进行合成。这里讨论一种特殊的情况，即多个简谐振动不仅方向相同、频率相同、振幅相同，而且依次间的相位差恒为Δφ。设多个简谐振动分别为

式中，A1=A2=…=AN=A0。由之前的讨论可以推知，这些简谐振动的合振动仍为简谐振动，设其表达式为

下面求合振动的振幅A和初相φ。

如图5-17所示，N个旋转矢量A1，A2，…，AN依次相接，∠OPB=Δφ。PO=PB=…=PQ=R，现在过点P作A1和A2的垂线，则两个垂线对点P所张的角就等于Δφ。根据多个矢量合成的法则，由点O指向点Q的矢量A就是合矢量，合矢量A对点P所张的角∠OPQ=NΔφ。于是由几何关系，有

图5-17　多个同方向同频率的等幅简谐振动的合成

上面两个式子相比，得合振动的振幅为

又由等腰三角形POQ及POB可得

从而得合振动的初相为

下面讨论两种特殊情况：

（1）当Δφ=2kπ（k=0，±1，±2，…）时，即多个同相位简谐振动的合成，由式（5-29）得

这种情况在矢量图中就是N个矢量A1，A2，…，AN的方向都相同，如图5-18所示，合振动的振幅最大，A=NA0。

图5-18　Δφ=2kπ（k=0，±1，±2，…）

（2）若NΔφ=2kπ（k=±1，±2，…，但不含N的整数倍），此时，在矢量图中N个矢量依次相接组成一个闭合的图形，如图5-19所示，显然合振幅应为零。

图5-19　NΔφ=2kπ（k=±1，±2，…，但不含N的整数倍）

多个同方向同频率的简谐振动的合成理论，在讨论光波、声波及电磁波的干涉和衍射时经常用到。

∗4.两个同方向不同频率简谐振动的合成

一质点同时参与两个同方向，频率分别为ν1、ν2的简谐振动，为了突出不同频率振动合成的结果，设这两个简谐振动的振幅相同，初相都是φ，并且ω2＞ω1，它们的分振动方程分别为

根据三角函数公式，合振动的位移为

显然，合振动不是简谐振动，对于ω2和ω1都比较大，而两者相差却很小的情况，有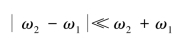，因此式（5-30）第一部分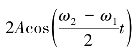随时间的变化比第二部分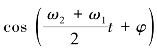随时间的变化慢很多，此时式（5-30）描述的是振幅随时间作缓慢变化的周期性运动。

这种振动方向相同、频率之和远大于频率之差的两个简谐振动合成时，合振幅随时间按周期性变化的现象称为拍，合振幅变化的频率称为拍频，用ν表示，它与周期的关系为T=。由于合振幅的周期为π，所以式（5-30）第一部分：

经比较有

所以拍频为

拍的应用是很广泛的，在各种声、电磁振动及无线电技术都有拍的应用，如用音叉校准钢琴的频率，原理是音调有微小差别就会出现拍音，调整到拍音消失，钢琴的一个键就被校准了。