阻尼振动、受迫振动和共振

简谐振动是一种等幅振动，它是不计阻力的理想情况。本节讨论物体受到弹性力、阻力或周期性外力作用时的振动情况。

1.阻尼振动

和前面讨论的简谐振动不同，实际生活中的振动总会受到阻力的作用，由于需要克服阻力做功，振动系统的能量不断地减少，在能量随时间减少的同时，振幅也随时间而减少，直到最后停止振动。振动系统因阻力作用，作振幅不断减小的振动，称为阻尼振动。

振动系统的阻尼通常分为两种：一种是由于摩擦阻力使系统的能量逐渐转化为热能，这叫作摩擦阻尼；另一种是振动以波的形式向外传播，使振动系统的能量逐渐向外辐射出去，转化为波的能量，这叫作辐射阻尼。本节主要讨论摩擦阻尼。

实验表明，当物体以不太大的速率在黏性介质中运动时，物体受到的阻力与其运动的速率成正比，即

式中，γ称为阻尼系数，它与物体的形状、大小及介质的性质有关，负号表示阻力与速度方向相反。对于弹簧振子，在弹性力F=-kx和阻力FR=-γv作用下，它的动力学方程为

或

令2β=和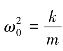，上式可写为

式（5-19）就是振动系统作阻尼振动的运动微分方程，其中是振动系统的固有圆频率，它由系统本身的性质所决定；称为阻尼系数，它与系统本身的性质及介质的阻尼系数有关，显然，β值越大，阻力的影响就越大，β值越小，阻力的影响就越小。β值的大小决定了振动系统的行为。

根据微分方程理论，因阻尼系数大小的不同，式（5-19）有三种不同形式的解，分别对应阻尼系统欠阻尼、临界阻尼和过阻尼三种不同的运动状态。

当阻尼系数较小，即β＜ω0时，系统处于欠阻尼状态，式（5-19）的通解为

式中，，表明圆频率比固有圆频率小，振幅为A e-βt是随时间作指数衰减，阻尼系数越大，振幅衰减得越快。欠阻尼状态下的位移-时间曲线如图5-13中的a曲线所示。

当阻尼系数很大，即β＞ω0时，式（5-19）的通解为

式中，C、D是由初始状态决定的积分常数。此时振子从初始状态缓慢地回到平衡位置，不再作周期运动，这称为过阻尼状态，它的位移-时间曲线如图5-13中的b曲线所示。

图5-13　三种阻尼的位移-时间曲线

a—欠阻尼；b—过阻尼；c—临界阻尼。

将弹簧振子放在黏度较大的油类介质中，就可以观察到弹簧振子在过阻尼状态下的运动。银行、宾馆等大型建筑的弹簧门上常装有一个消振油缸，消振油缸的作用就是避免弹簧门来回振动，使它工作在过阻尼状态。(www.xing528.com)

当β=ω0时，式（5-19）的通解为

式中，A、B是由初始状态决定的常数。此时阻尼大小恰好使振子开始作非周期振动，与欠阻尼和过阻尼状态相比，这种状态下振动系统从开始振动的状态回到平衡位置所经过的时间最短。此称为临界阻尼状态，其位移-时间曲线如图5-13中c曲线所示。在陀螺经纬仪、灵敏电流计、精密天平等一些精密仪器中广泛采用临界阻尼系统，使仪器指针尽快停到应指示的位置。

2.受迫振动

实际的振动系统由于受到阻力而消耗能量，会使振幅不断衰减。要使振动持续不断地进行，必须对振动系统施加一周期性外力，使系统不断得到能量补充，这种周期性外力叫驱动力。欠阻尼振动系统在持续的周期性外力作用下进行振动称为受迫振动。例如，钟摆的振动，机器运转时所引起的基座的振动都是受迫振动。

设一系统在弹性力-kx，阻力-γv和周期性外力F0cosωt的作用下作受迫振动，则振动系统的动力学方程为

上式也可写为

令0，则振动方程可写为

式（5-23）的通解为

式（5-24）表明受迫振动是由阻尼振动和简谐振动A cos（ωt+φ）合成的。阻尼振动是减幅振动，经过一段时间后这一振动就衰减到可以忽略不计，受迫振动达到稳定状态，变为等幅的简谐振动。式（5-24）中振动的圆频率ω就是驱动力的圆频率，振幅A和初相分别为

由于周期性外力的初相为零，因此这里的初相就是稳定振动状态与驱动力的相位差，对此我们不做深入讨论。

3.共振

由式（5-24）可知，受迫振动的振幅与驱动力的圆频率有关。当驱动力的圆频率为某一定值时，振幅A达到最大值。我们把驱动力的圆频率为某一定值时，受迫振动的振幅达到最大的现象叫作共振，共振时的圆频率叫作共振圆频率，用ωr表示，可用求极值的方法求得。根据=0，可得

相应的最大振幅为

由此可知，系统的共振圆频率是由固有圆频率ω0和阻尼系数β决定的。当β≪ω0，ωr接近系统的固有圆频率ω0时，共振振幅趋于无穷大。图5-14是不同阻尼情形共振振幅随ω变化的曲线。

图5-14　不同阻尼情形共振振幅随ω变化的曲线

共振在声学、光学、无线电技术等方面的应用是很普遍的。例如，钢琴、小提琴等乐器利用共振来提高音响效果，收音机的调谐装置也是利用电磁共振进行选台。共振也有其危害性，共振时因为系统振幅过大会造成建筑物、机械设备的损坏等。历史上也曾有部队迈着整齐的步伐过桥时，大桥坍塌的惨剧发生。因此，在生活中我们可以利用共振或者避免发生共振来解决实际的问题。