简谐振动能量-大学物理教程

本节以弹簧振子为例来讨论简谐振动的能量。设质量为m，劲度系数为k的弹簧振子，在某一时刻的位移为x，速度为v，则

又有，则可得弹簧振子所具有的振动动能和振动势能分别为

式（5-14）和式（5-15）说明弹簧振子的动能和势能是按余弦或正弦的平方随时间变化的，图5-12表示初相为零时，动能、势能和总机械能随时间变化的曲线。显然，动能最大时，势能最小；而动能最小时，势能最大。简谐振动的过程正是动能和势能相互转换的过程。

图5-12　简谐振动动能、势能和总机械能随时间变化的曲线

将式（5-14）和式（5-15）两式相加，即得简谐振动的总机械能为

可见，简谐振动系统在振动过程中机械能守恒。从力学角度看，简谐振动系统都是孤立的保守系统。另外，从式（5-16）可以得出简谐振动是等幅振动，其能量正比于振幅的平方、正比于系统固有圆频率的平方。

动能在一个周期内的平均值为

同理，可得

所以动能和势能在一个周期内的平均值相等，且等于总机械能的一半。

以上结论虽是由弹簧振子这一特例推出，但具有普遍意义，适用于任何简谐振动系统。

例5-6　质量为0.1 kg的物体，以振幅3.0×10-2m作简谐振动，其最大加速度为12.0 m·s-2，求该物体：(www.xing528.com)

（1）振动的周期；

（2）通过平衡位置时的动能；

（3）具有的总机械能；

（4）在何处动能和势能相等。

解　（1）因为amax=Aω2，故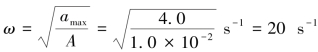，得

（2）因通过平衡位置的速度为最大，故

（3）总机械能为

（4）由Ek=Ep，E=Ek+Ep，得

将Ep=kx2代入上式，得

则x=±A=0.707×10-2m，即在该处物体的动能和势能相等。