简谐振动：初相求解-大学物理教程

物体在一定位置（平衡位置）附近的往复运动称为机械振动，如海浪、地震等。振动不只限于机械振动，广义上讲，任何一个描述物体运动状态的物理量在某一量值附近随时间作周期性变化都可以叫作振动，如交流电路中的电压和电流，电磁场中电场强度和磁感应强度等都是振动。振动的形式多种多样，大多数情况比较复杂，简谐振动是最简单、最基本的振动，任何复杂的振动都可以认为是由许多简谐振动合成的。

1.简谐振动的特征

一个作往复运动的物体，如果其偏离平衡位置的位移x（或角位移θ）随时间t按余弦（或正弦）规律变化，即

则这种振动称为简谐振动。

研究表明，作简谐振动的物体（或系统），尽管描述它们偏离平衡位置位移的物理量可以千差万别，但描述它们动力学特征的运动微分方程则是相同的。

下面以弹簧振子来演示，将轻质弹簧（质量可忽略不计）一端固定，另一端系一个可以自由运动的物体所组成的系统称为弹簧振子。图5-1所示为一个放置于光滑水平面上的弹簧振子，当质量为m的物体位于点O时弹簧处于自然状态（未伸长未压缩状态），此时，物体在水平方向所受合外力为零，则点O称为平衡位置，并取为坐标原点，水平向右为坐标系x轴正向。

图5-1　弹簧振子

由胡克定律可知，物体所受的弹力F与物体相对平衡位置的位移x成正比，其方向始终指向平衡位置，与位移方向相反，这种力被称为回复力。

设弹簧的劲度系数为k，物体的质量为m，不计各种阻力，当振子偏离平衡位置的位移为x时，其受到的弹性力为

根据牛顿第二定律，则弹簧振子的运动微分方程为

令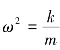，则有

式（5-4）的解可写成余弦函数形式，即式（5-1），式（5-1）中A和φ0是由初始条件确定的两个积分常数。式（5-4）是描述简谐振动的运动微分方程。

由于

令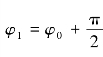，则式（5-1）也可写为

式（5-4）的解也可写成正弦函数形式，即式（5-5），本教材对机械振动统一用余弦函数表示。

由此，我们可以给出简谐振动的一种较普遍的定义：如某力学系统的动力学方程可归结为式（5-4）的形式，且其中常量ω仅取决于系统本身的性质，则该系统的运动为简谐振动，能满足式（5-4）的系统，又可称为谐振子系统，这是简谐振动的运动学特征。

如果物体离开平衡位置后，受到一个方向总是指向平衡位置，大小与位移成正比的力，那么这个物体也一定在作简谐振动，这是简谐振动的动力学特征。

将式（5-1）对时间分别求一阶和二阶导数，可得到简谐振动物体的速度和加速度的表达式分别为

由式（5-1）、（5-6）、（5-7）可知，物体作简谐振动时，它的位移、速度和加速度都是周期性变化的，且速度和加速度具有相同的变化频率。位移的最大值为A，速度的最大值为ωA，加速度的最大值为ω2A，简谐振动位移、速度、加速度随时间的变化曲线，如图5-2所示。

图5-2　简谐振动位移、速度、加速度随时间的变化曲线

2.简谐振动的振幅、周期、频率和相位

1）振幅

x=A cos（ωt+φ0）中A表示振动物体偏离平衡位置的最大距离，它表明了振动的幅度或振动的空间范围，这个量称为简谐振动的振幅，用符号A表示，振幅恒取正值。在图5-1描述的简谐振动中，移动物体离开平衡位置越远，则放开后物体的振幅就越大，可见，振幅的大小取决于振动系统的初始状态。对于弹簧振子的简谐振动，将t=0时的初始条件x=x0、v=v0代入x=A cos（ωt+φ0）、v=-ωA sin（ωt+φ0），有x0=A cosφ0和v0=-Aωsinφ0，联立求解得

2）周期、频率

物体作简谐振动时，周而复始完成一次全振动所需的时间叫作简谐振动的周期，用T表示。由周期的性质，有

由于余弦函数的周期是2π，所以有ωT=2π，因此

和周期密切相关的另一物理量是频率，即单位时间内系统所完成的完全振动的次数，用ν表示，即

式中，ω表示系统在2πs内完成的完全振动的次数，称为圆频率（又称角频率）。在国际单位制中，周期T的单位是s，频率ν的单位是Hz，圆频率ω的单位是rad·s-1。

质量m和劲度系数k都属于弹簧振子本身的固有性质，T、ν或ω都表示简谐振动的周期性特征，完全取决于弹簧振子本身的性质。因此T、ν、ω分别称为系统的固有周期、固有频率、固有圆频率。

3）相位(www.xing528.com)

当振幅A和圆频率ω一定时，物体在任一时刻的运动状态取决于（ωt+φ0）。量值（ωt+φ0）叫作振动的相位。相位是决定简谐振动物体运动状态的物理量，一定的相位对应着一个确定的运动状态。例如，当ωt1+φ0=时，x=0，v=-ωA，表示在t1时刻物体处在平衡位置，并以速度ωA向x轴负向运动；而当ωt2+φ0=π时，x=0，v=ωA，即在t2时刻物体也在平衡位置，但以速度ωA向x轴正向运动。可见由于振动的相位不同，物体的运动状态也不相同。

t=0时的相位叫初相位，简称初相。由式（5-1）和式（5-6）得初相和初始条件之间的关系为

可见，初相是由初始条件确定的，初相的范围为-π～+π。

设有两个频率相同的简谐振动，它们的运动学方程分别为

两个简谐振动的相位之差称为相位差，用Δφ表示，它的数值为

当Δφ=2kπ（k=0，±1，±2，…），即相位差为零或π的偶数倍时，两个简谐振动的步调一致，称为同相。而当Δφ=（2k+1）π（k=0，±1，±2，…），即相位差为π的奇数倍时，两个简谐振动的步调相反，称为反相。

如果Δφ＞0，即φ2＞φ1，称简谐振动2的相位超前简谐振动1的相位，或简谐振动1的相位滞后简谐振动2的相位。

例5-1　已知一简谐振动方程，t=0时，x=0，v0＜0，示意图如图5-3所示，求初相φ0。

图5-3　例5-1图

解　设简谐振动方程为

将t=0时，x=0代入，可得

则可得

又因为v0=-Aωsinφ0＜0，所以

因此

例5-2　假设有一质点作简谐振动，其振动方程为

求振动的振幅、频率和初相，并求t=0.5 s时的位移和速度。

解　把该振动方程与x=A cos（ωt+φ0）比较可得

振幅：A=9×10-2m；圆频率：ω=10πrad·s-1；频率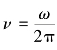：=5 Hz；初相：φ0=0.25π。

把t=0.5 s带入该振动方程，该时刻的位移为

则速度为

则t=0.5 s时的速度为

例5-3　一轻弹簧一端固定，另一端连接一定质量的物体。整个系统位于水平面内，系统的圆频率为6.0 rad·s-1，今将物体沿平面向右拉长到x0=0.04 m处由静止释放，试求：（1）简谐振动方程；（2）物体从初始位置运动到第一次经过A/2处时的速度。

解　（1）一轻质弹簧连接一物体，满足简谐振动，设简谐振动方程为

由初始条件得振幅和初相为

（2）由题意画出图，如图5-4所示。

图5-4　例5-3图

将A/2代入求得的振动方程，得

则或者，速度v=-Aωsinωt=±0.208 m·s-1，按题意得