大学物理教程：位置矢量、位移、速度和加速度详解

1.位置矢量

描述质点在空间所处位置的矢量称为位置矢量，一般为坐标系的原点指向质点所在位置的有向线段，位置矢量也称为位矢或矢径。在如图1-3所示的直角坐标系中，在时刻t，质点P在坐标系里的位置可用位矢r（t）来表示。

图1-3　位置矢量

位矢是一个有向线段，其始端位于坐标系的原点O，末端则与质点P在时刻t的位置重合。从图中可以看出，位矢r在x轴、y轴和z轴上的投影（即质点的坐标）分别为x、y和z。所以，质点P在直角坐标系中的位置，既可以用位矢r来表示，也可以用坐标x、y和z来表示。那么位矢r亦可写成

其大小为

位矢r的方向余弦由下式确定：

当质点运动时，质点的坐标x、y、z和位矢r是随时间而变化的。因此，质点的坐标x、y、z和位矢r是时间的函数，即

式（1-9）叫作质点的运动方程；而x=x（t），y=y（t），z=z（t）称为运动方程的分量式，从中消去参数t可得到质点运动的轨迹方程，所以它们也是轨迹的参数方程。

应当指出，运动学的重要任务之一就是找出各种具体运动所遵循的运动方程。

2.位移

如图1-4所示，在平面直角坐标系Oxy中，有一质点沿曲线从时刻t1的点A运动到时刻t2的点B，质点相对原点O的位矢由rA变化到rB。显然，在时间间隔Δt=t2-t1内，位矢的长度和方向都发生了变化。我们将由点A指向点B的有向线段称为在时间间隔Δt内质点的位移矢量，简称位移。位移反映了在时间间隔Δt内质点位矢的变化。

图1-4　位移

如把写作Δr，则质点从点A到点B的位移为

亦可写成

式（1-11）表明，当质点在平面上运动时，它的位移等于在x轴和y轴上的位移矢量和。

若质点在三维空间运动，则在直角坐标系Oxyz中其位移为

应当注意，位移是描述质点位置变化的物理量，并非质点所经历的路程。如在图1-4中，曲线所示的路径是质点实际运动的轨迹，轨迹的长度为质点所经历的路程Δs，而位移则是Δr。当质点经一闭合路径回到原来的起始位置时，其位移为零，路程则不为零。所以，质点的位移和路程是两个完全不同的概念。只有在Δt趋近于零时，位移的大小dr才可视为与路程ds相等。

3.速度

在研究质点的运动时，若仅知道质点在某时刻的位矢，则不能同时知道该质点是静还是动，即其运动状态是不明确的。所以，还应引入一物理量来描述位矢随时间的变化程度，这就是速度。力学中，只有当质点的位矢和速度同时被确定时，其运动状态才被确定。

1）平均速度

如图1-5所示，一个质点在平面上沿轨迹CABD曲线运动。在时刻t，它处于点A，其位矢为r1（t）；在时刻t+Δt，它处于点B，其位矢为r2（t+Δt）。在时间间隔Δt内，质点的位移为Δr=r2-r1。

图1-5　平均速度、速度

在时间间隔Δt内的平均速度为

显然，平均速度的方向与位移Δr相同。

又因为

平均速度可写成

其中是平均速度在x轴和y轴上的分量。

2）瞬时速度

显然，用平均速度描述物体的运动是比较粗糙的。因为在时间间隔Δt内，质点各个时刻的运动情况不一定相同，质点的运动可以时快时慢，方向也可以不断改变。如果要精确地知道质点在某一时刻（或某一位置）运动的快慢和方向，应使Δt尽量减小而趋近于零，用平均速度的极限值来描述。

当Δt→0时，平均速度¯v的极限值叫作瞬时速度（简称速度），用v表示，有

vx和vy是速度v在x轴和y轴上的分量，又称为速度分量（注意：它们是分矢量！）。

速度v的方向与Δr在Δt→0时的极限方向一致。当Δr在Δt→0时，Δr趋于和轨迹相切，即与点A的切线重合。所以当质点作曲线运动时，质点在某一点的速度方向，就是沿该点曲线的切线指向质点前进的方向。

3）平均速率和瞬时速率

速度是矢量，具有大小和方向。描述质点运动时，如果不考虑运动的方向，我们常采用一个叫作“速率”的物理量。在Δt时间内，质点所经历的路程为Δs，那么Δs与Δt的比值就称为质点在Δt时间内的平均速率，即

当Δt尽量减小而趋近于零时，平均速率的极限值就是质点的瞬时速率（简称速率），即

可见，速率就是速度的大小，而不考虑方向。

因此，在一般曲线运动中速度亦可表示为

其中，et为此时速度方向上的单位矢量，如图1-6所示。

图1-6　速度

当质点的位矢和速度同时被确定时，其运动状态也就被确知。因此，位矢r和速度v是描述质点运动状态的两个物理量。这两个物理量可以从运动方程求出，所以知道了运动方程就能确定质点在任意时刻的运动状态。因此，概括说来，运动学问题有两类：一是由已知运动方程求解运动状态；二是由已知运动状态求解运动方程。

例1-1　一质点沿x轴作直线运动，其运动方程为x=10+4t-t2，式中x的单位为m，时间t的单位为s。求：（1）质点从第1 s末到第3 s末的位移和平均速度；（2）质点在第3 s末的速度。

解　这是一维直线运动，故矢量号可略去。

（1）质点的运动方程为x=10+4t-t2，将t=1 s和t=3 s分别代入，得出质点第1 s末和第3 s末在x轴上的位置分别为

可见质点从第1 s末到第3 s末的位移为

质点从第1 s末到第3 s末的平均速度为

（2）质点任一时刻的速度为

将t=3 s代入，得质点在第3 s末的速度v3=-2 m·s-1，即质点在第3 s末的速度大小为2 m·s-1，方向沿x轴的负方向。

例1-2　一质点在Oxy平面上运动，其运动方程为x=2t，y=6-2t2，式中x、y的单位为m，时间t的单位为s。求：（1）质点从第1 s末到第2 s末的位移和平均速度；（2）质点在t=1 s时刻的速度；（3）质点的轨迹方程。（所求位移、平均速度、速度均用直角坐标系中的矢量式表示。）

解　由题意，质点任一时刻的位矢为

（1）将t=1 s和t=2 s分别代入，得出质点在第1 s末和第2 s末的位矢分别为

则质点从第1 s末到第2 s末的位移为

质点从第1 s末到第2 s末的平均速度为

（2）质点任一时刻的速度为

将t=1 s代入，得出质点在t=1 s时刻的速度为(www.xing528.com)

（3）由已知运动方程x=2t，y=6-2t2，消去t可得质点的轨迹方程为

例1-3　设质点的运动方程为r（t）=x（t）i+y（t）j，其中x（t）=1.0t+2.0，y（t）=0.25t2+2.0，式中x、y的单位为m，时间t的单位为s。（1）求t=3 s时的速度；（2）作出质点的运动轨迹图。

解　（1）由题意可得速度分量分别为

故质点在t=3 s时刻的速度分量为

于是t=3s时，质点的速度为

速度的值为=1.8 m·s-1，速度v与x轴之间的夹角为

（2）由已知运动方程x（t）=1.0t+2.0，y（t）=0.25t2+2.0，消去t可得轨迹方程为并可作如图1-7所示的质点运动轨迹图。

图1-7　例1-3图

4.加速度

上面已经指出，作为描述质点状态的一个物理量，速度是一个矢量，所以，无论是速度的数值发生改变，还是其方向发生改变，都表示速度发生了变化。为描述速度的变化，我们引出加速度的概念。

1）平均加速度

如图1-8所示，设在时刻t，质点位于点A，其速度为v1；在时刻t+Δt，质点位于点B，其速度为v2。则在Δt时间内，质点的速度增量为Δv=v2-v1，它在单位时间内的速度增量即平均加速度为

图1-8　加速度

2）瞬时加速度

平均加速度只是反映在Δt时间内速度的平均变化率。为了精确地描述质点在任意时刻t（或任一位置）的速度变化率，就必须引入瞬时加速度的概念。

当Δt→0时，平均加速度的极限值叫作瞬时加速度，简称加速度，用a表示，有

a的方向是Δt→0时Δv的极限方向，而a的数值是Δt→0时的极限值。

应当注意，加速度a既反映了速度方向的变化，也反映了速度数值的变化。所以质点作曲线运动时，任一时刻质点的加速度方向并不与速度方向相同，即加速度方向不沿着曲线的切线方向，而是与速度变化的方向相同。在曲线运动中，加速度的方向指向曲线的凹侧。

在平面直角坐标系中，加速度公式可以写成

例1-4　对例1-2所讨论的质点运动，求：（1）质点从第2 s末到第3 s末的平均加速度；（2）质点任意时刻的加速度。（所求各量均用直角坐标系中的矢量式表示。）

解　（1）质点任一时刻的速度为

将t=2 s和t=3 s分别代入，得出质点在第2 s末和第3 s末的速度分别为

故质点从第2 s末到第3 s末的平均加速度为

（2）由得，质点任一时刻的加速度为

思考本题中质点的运动性质。

例1-5　一质点在Oxy平面上运动，其运动方程为x=3t+5，y=0.5t3+3t-4，式中x、y的单位为m，时间t的单位为s。求：（1）质点从t=0时刻到t=4 s时刻的平均加速度；（2）质点在t=4 s时刻的加速度。

解　（1）由题意知，质点任一时刻的位矢为

故质点任一时刻的速度为

将t=0和t=4 s分别代入，得出质点在t=0时刻和t=4 s时刻的速度分别为

则质点从t=0时刻到t=4 s时刻的平均加速度为

可见质点从t=0时刻到t=4 s时刻的平均加速度值为6 m·s-2，方向沿y轴的正方向。

（2）由得，质点任一时刻的加速度为

将t=4 s代入，得质点在t=4 s时刻的加速度为12j m·s-2，即值为12m·s-2，方向沿y轴的正方向。

5.运动学的基本问题

运动学的问题一般分为两大类：第一类问题是已知质点的运动方程，求质点任意时刻的速度和加速度；第二类问题是已知质点的加速度和初始条件，反过来求质点的速度和运动方程。

第一类问题可以通过运动方程对时间的逐级求导得到。

例1-6　质点的运动方程为

式中，x、y的单位为m；t的单位为s。

试求：（1）初速度的大小和方向；（2）加速度的大小和方向。

分析　由运动方程的分量式可分别求出速度、加速度的分量，再由运动合成算出速度和加速度的大小和方向。

解　（1）速度的分量式为

当t=0时，v0x=-10 m·s-1，v0y=15 m·s-1，则初速度大小为

设v0与x轴的夹角为α，则

（2）加速度的分量式为

则加速度的大小为

设a与x轴的夹角为β，则

第二类问题则是通过对加速度积分而得到结果，积分常数要由问题给定的初始条件，如初始位置和初始速度来确定。

例1-7　质点沿直线运动，加速度a=4-t2，式中a的单位为m·s-2，t的单位为s。如果当t=3 s时，x=9 m，v=2 m·s-1，求质点的运动方程。

分析　本题属于运动学第二类问题，即已知加速度求速度和运动方程，必须在给定条件下用积分方法解决。由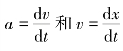可得dv=adt和dx=vdt。如a=a（t）或v=v（t），则可两边直接积分。

解　由分析知，应有

将t=3 s时，x=9 m，v=2 m·s-1代入式（1-27）和式（1-28）得：v0=-1 m·s-1，x0=0.75m。于是可得质点的运动方程为

例1-8　一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即=-Kv2，式中K为常量。试证明电艇在关闭发动机后又行驶x距离时的速度为

其中v0是发动机关闭时的速度。