高速动车组齿轮箱叠加法理论研究

1.准静态叠加法

在工程分析中，确定了载荷工况和边界条件就能运用有限元法计算得到结构的应力与变形。准静态叠加法是一种在结构受到外部随机载荷作用时的线性分析法，该方法假设忽略结构本身的弹性振动及其部件质量、惯量等特性，即忽略惯性力和阻尼力的作用，使用的边界条件为：结构件刚度很大而外界激励频率无法使其产生共振，且结构件在受到外载荷时基本处于平衡状态。该方法的基本原理是：结构件在受到外部随机载荷的位置处施加与随机激励同向的单位静载荷，通过计算分析得到结构的静应力影响因子，然后用结构件受到的外部随机载荷与静应力影响因子相乘，得到结构件的动应力。当多个外部载荷同时作用在结构件上时，结构件的总动应力由单个随机载荷获得的动应力线性叠加[110]。

式（2-44）为该方法在假定平面应力条件下，结构某节点的应力时间历程计算的数学公式[111]。

式中，n为应用载荷历程数量；σxi，σyi，τxyi为应力影响因子，i∈[1,n]，应力影响因子由施加在结构件部件与载荷历程作用在相同位置和方向的单位载荷决定。

准静态法作为常用的时域分析法，用于外界载荷频率远离结构件固有频率的刚性结构。这对于工作在固有频率之下的刚性结构是一种有效的应力分析方法，但当结构柔性较大时，动力学因素对其影响较大，导致疲劳寿命计算结果与实际值存在较大差异，所以很少应用。

2.模态叠加法

模态叠加法通常用来求解结构件的动力响应。首先建立结构件的有限元模型并计算其模态，接着将动力学方程解耦，通过线性变换将结构件的模态坐标响应转变为物理坐标响应[112]。在实际运行中，往往是低阶模态对结构件影响较大，因此为了降低计算量，只需考虑结构件的前几阶低阶模态即可。

系统动力学的基本方程为[113]

式中，为评估点加速度向量；为评估点速度向量；｛u｝为评估点位移向量；｛P（t）｝为外载荷时间历程；[M]为质量矩阵；[B]为阻尼矩阵；[K]为刚度矩阵。(www.xing528.com)

将运动方程从物理坐标｛u｝变换为模态坐标｛q｝：

式中，[φ]为振型矩阵。模态叠加法理论中系统振动应重点考虑前几阶主模态的主导作用，且这几阶模态的计算精度都较高。

将式（2-46）代入式（2-45）得到模态坐标下的运动方程：

将两边左乘，得到新的向量空间内的运动方程：

式中，为广义质量矩阵；为广义阻尼矩阵；为广义刚度矩阵；为模态力向量。

利用振型正交特性，将式（2-48）写成式（2-49）所示的一系列单自由度系统方程：

式中，为模态阻尼比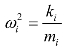；为模态频率。