频率混叠及其在动车组齿轮箱振动中的影响

如果对传感器设置的采样频率为F，通过傅里叶变换后，频谱图中能够显示的频率为F/2，而信号中F/2以上的频率成分信息并没有消失，而是对称地映射到F/2以下的频带中，并且与F/2以下的原有频率成分叠加起来，这种现象称为混叠[104]（aliasing），如图2-1所示。

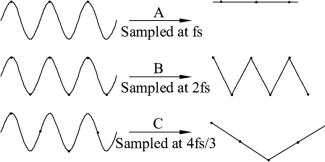
图2-1　频率混叠原理

如果原始信号的实际频率为fs，根据图2-1中的3种情况，则有：

（1）采样频率F为fs时，采样得到的信号为一条直线，频率为0；

（2）采样频率F为2fs时，采样得到的信号为谐波信号，频率为fs；

（3）采样频率F为4fs/3时，采样得到的信号依然为谐波信号，频率为fs/3，出现频率混叠。

实际信号频率为fs，采取频率为F，并且F＜2fs，经采样分析得到混叠频率为fa，则根据混叠机理，可以得到分析信号的混叠频率的计算公式：(www.xing528.com)

式中，n=int(fs/F+0.5)，其中int()为取整数操作，即n为与被混叠信号f最接近的采样频率整数倍所对应的整数。

频率混叠是由于采样信号频谱发生变化而出现高、低频成分发生混淆的一种现象。采样频率不够高，采样的数据包括信号中的低频和高频信号的样本值，这使得信号重建时出现高频信号被低频信号代替，导致两种波形完全重叠在一起，形成严重失真。频率混叠是数字信号处理中的一个重要概念和一种特有现象，由数字信号中离散采样引起。通常等步长离散采样或采样频率小于模拟信号或实测信号频率的2倍就会产生频率混叠现象，该现象在本书第3章中对轴箱开展时频分析时会多次出现。

避免或减小频率混叠的措施：

（1）提高采样频率，使之达到最高信号频率的两倍以上，使混叠信号发生在需要考虑或研究的频域区间之外；但提高采样频率会使频率分辨率降低，而频率分辨率与采样时间有关联性，所以应选择合理的采样频率。

（2）引入低通滤波器或提高低通滤波器的参数。该低通滤波器通常称为抗混叠滤波器，可限制信号的带宽，使之满足采样定理的条件，所以引入抗混叠滤波器是减少混叠发生较为有效的办法。

（3）采用不等步长采样信号也可减少混叠的发生。