【摘要】：连续小波变换在时域定义为[102]式中，a≠0，为尺度因子；b为时移因子，函数w为母小波。小波变换优于傅里叶变换的地方在于其可以分析信号的局部特征，而傅里叶变换着重研究信号的整体特征。小波函数在允许的条件下能够根据信号的特征进行构造，具有较强的灵活可变性，而傅里叶变换只是用正、余弦函数来展开信号。
小波分析法是一种窗面积固定但其形态可改变，时间窗和频率窗均可变化的时频局部化分析方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率。
小波变换的基本思想与傅里叶变换类似，即用信号在一簇基函数形成的空间投影来表征该信号，但这一簇函数是通过基本母子波函数中不同尺度的伸缩和平移构成，其时宽和频宽积很小，且在时间和空间上很集中。
连续小波变换在时域定义为[102]
式中，a≠0，为尺度因子；b为时移因子，函数w(t)为母小波。用不同的a和b构成的小波基函数：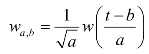
，小波逆变换为
小波变换在频域可以表示为
式（2-7）中，F-1表示傅里叶逆变换。
如果w(t)表示为
则w(t)的傅里叶变换W(f)为(www.xing528.com)
现在证明式（2-5）和式（2-7）是完全等价的。
由于
式（2-7）可写为
式（2-12）的中括号积分项可写为
将式（2-13）代入式（2-12）可得
可以看出，式（2-14）和式（2-5）完全相同，因此式（2-5）和式（2-7）等效。
小波变换优于傅里叶变换的地方在于其可以分析信号的局部特征，而傅里叶变换着重研究信号的整体特征。小波函数在允许的条件下能够根据信号的特征进行构造，具有较强的灵活可变性，而傅里叶变换只是用正、余弦函数来展开信号。小波分析应用联合时间-尺度函数分析非平稳信号，分析的非平稳信号是在时间-尺度平面上，因此小波分析是一种特殊的时频分析。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
