汽车车身设计质量控制-拼焊板车门稳健性控制

目前的汽车结构轻量化研究多集中在轻量化途径上，而忽略了轻量化汽车性能的稳健性。实际上，汽车的制造和使用过程存在许多不确定性因素，当设计变量波动时，可能导致汽车性能指标超出约束边界或者对变量的波动极为敏感，从而降低汽车的品质。

车门是汽车最重要的大型覆盖件之一，在车身质量中占有较大的比例，对车门进行轻量化研究，不仅可以一定程度上减小车身质量，而且可以为整车的轻量化研究提供参考。拼焊板技术是汽车轻量化发展方向之一，具有诸多优势和广泛的应用前景。目前有关拼焊板技术在车门上的应用研究大多集中在拼焊板成形工艺和厚度优化上，而未对拼焊线位置及其对车门品质的影响进行研究。车门系统是一个复杂繁琐的系统，对车门进行轻量化设计需要考虑诸多因素的影响。传统的车门轻量化设计把它当做确定性优化问题，即在约束条件下寻找确定性最优解。事实上，车门的制造和使用过程存在许多不确定性因素，如生产精度、材料特性和载荷状况等，导致车门的品质特性响应（如刚度、强度和模态等性能）表现为概率分布，使得设计可能超出约束条件致使设计失效。稳健性优化设计通过减少响应偏差来满足约束条件。6σ稳健性优化设计是一种将6σ质量控制准则、可靠性优化和稳健性设计相结合的现代设计方法，它要求产品质量在均值6σ范围内波动时均能满足设计要求，从而使产品可靠度达到99.99966%。将6σ稳健性优化设计和车门轻量化结合起来，可以在减小车门质量的同时保证车门品质的稳健性。

在工程优化设计中，需要进行多次迭代，如果设计变量的任何改变均需试验或仿真分析，将会造成资源和时间的极大消耗。鉴于此，利用试验设计，构造出高精度的响应面模型，结合连续二次规划优化方法和蒙特卡罗模拟技术，提出基于6σ稳健性优化的车门轻量化方法。研究结果表明，这种方法既提高了计算效率，又减小了车门质量，同时还有效地保证了车门品质的稳健性。

图6-52为该前车门的有限元模型，由拼焊板内板、外板、三块内外板加强板、铰链、防撞梁、铰链加强板及玻璃导轨等零件组成。内外板之间通过包边工艺连接，外板加强板焊接在内板上，并通过胶粘与外板连接。

图6-52 前车门模型和下垂刚度工况

车门应当具有足够的刚度、强度和良好的抗振特性等力学性能，以保证汽车的安全性和乘坐舒适性。衡量车门的刚度有多个评价指标，下垂刚度是最重要的一个。下垂刚度不足可能导致车门下沉量过大，从而造成漏风、漏水和段差过大等品质问题。一阶扭转模态是评价车门抗振特性的重要指标，良好的扭转模态性能可以有效地提高车门抗扭能力并降低车门异响等品质问题。

下垂刚度工况如图6-52所示：约束车门副铰链6个方向自由度以及锁心处y向平动自由度，主副铰链之间放开绕z轴旋转自由度，在锁心处施加z向900N的力，用K=F/s评价下垂刚度，其中F为900N，s为锁心z向位移量，K越大则下垂刚度越好。根据该车型车门与侧围的间隙段差的控制及门系统刚度标准，s应小于5mm，则K应大于180N/mm。

一阶扭转模态：约束车门副铰链6个方向自由度以及锁心处x、y、z三个方向平动自由度，主副铰链之间放开绕z轴旋转自由度，计算车门一阶扭转模态频率f。根据该车型整车模态规划表，f应该大于45Hz，否则可能与车身低阶模态耦合共振。

1.稳健性控制过程

为了构造出高精度的车门质量m、下垂刚度K和一阶扭转模态频率f的响应面近似模型，从众多影响因素中筛选出主要的几个因数非常重要。通过下垂刚度和一阶扭转模态的灵敏度分析，定义外板厚度、内板拼焊板两个厚度、内外板加强板厚度、铰链加强板厚度和拼焊线x轴坐标等6个变量。

拼焊线位置变量的定义如图6-53所示：在Hy-permesh中，利用Hypermorph功能，将拼焊线定义为edge domain（即图中的L线），通过控制L线两端的handles（即图中的A、B）调节L线的位置，从而实现拼焊线位置的移动。为了减少变量数目，设区域D的拼焊线位置不变，且拼焊线的x轴坐标相同，则定义L线的x轴坐标值为拼焊线位置变量。

综合考虑车门的成本和工艺要求：厚度变量应该为0.6～1.8mm，拼焊线x轴坐标应该为1550～1600。根据工程经验和参考相关文献，各设计变量均服从正态分布，取值范围和标准差见表6-12。

图6-53 拼焊线位置变量定义示意图

表6-12 设计变量表

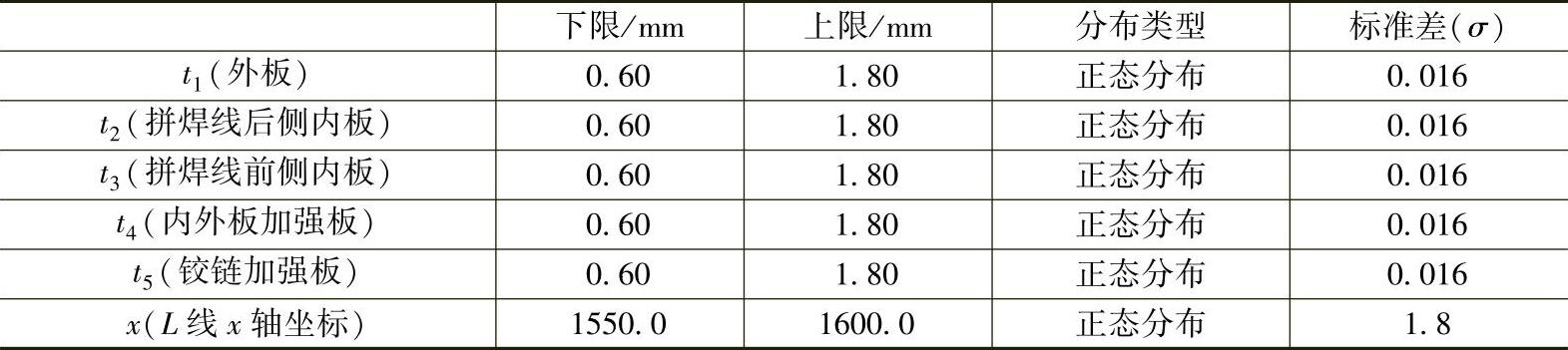
整个优化过程流程图如图6-54所示，首先根据产品设计要求确定变量、约束和目标，然后在优化软件HyperStudy中进行试验设计，建立约束和目标函数的响应面模型，并检查响应面的精度，最后在优化软件iSIGHT中进行该问题的确定性优化和6σ稳健性优化。

该问题的确定性优化数学模型如下：

图6-54 优化过程的流程图

min m

s.t. K≥180

f≥45

d.v. 0.6≤t₁≤1.8

0.6≤t₂≤1.8(www.xing528.com)

0.6≤t₃≤1.8

0.6≤t₄≤1.8

0.6≤t₅≤1.8

1550≤x≤1600

相应的6σ稳健性优化数学模型为：

min μ[m]+6σ[m]

s.t. μ[K]-6σ[K]≥180

μ[f]-6σ[f]≥45

d.v. 0.6+6σ[t₁]≤μ[t₁]≤1.8-6σ[t₁]

0.6+6σ[t₂]≤μ[t₂]≤1.8-6σ[t₂]

0.6+6σ[t₃]≤μ[t₃]≤1.8-6σ[t₃]

0.6+6σ[t₄]≤μ[t₄]≤1.8-6σ[t₄]

0.6+6σ[t₅]≤μ[t₅]≤1.8-6σ[t₅]

1550+6σ[x]≤μ[x]≤1600-6σ[x]

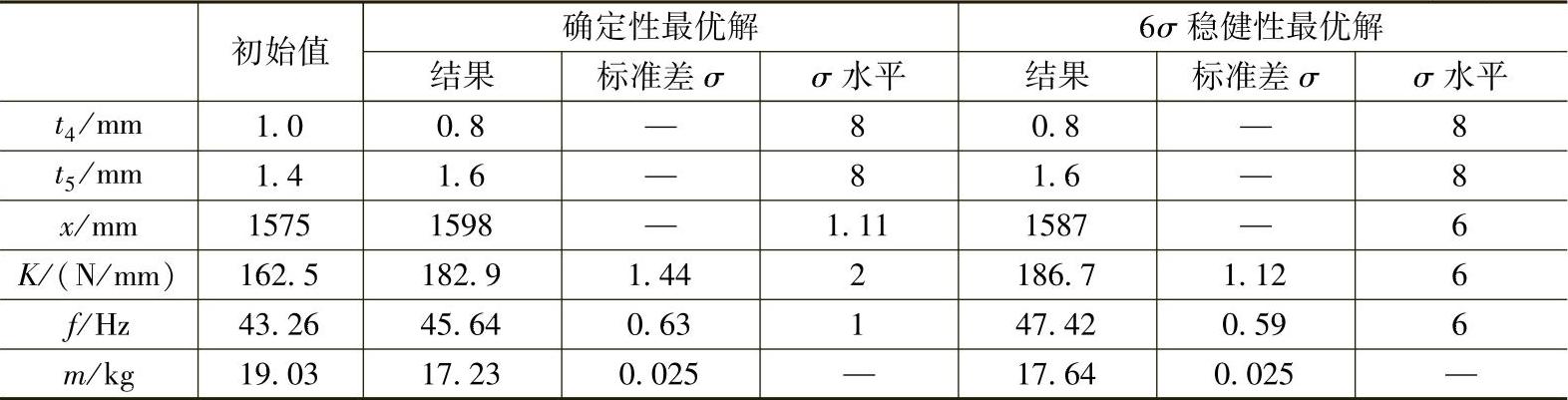
在初始设计条件下（表6-13），车门的质量为19.03kg，下垂刚度为162.5N/mm，一阶扭转模态频率为43.26Hz，车门偏重且下垂刚度和一阶扭转模态不满足约束条件，因此需要对该门进行优化设计。采用均匀拉丁方试验设计，通过40个试验点构造车门质量m、下垂刚度K和一阶扭转模态频率f的二次响应面模型，m、K和f的决定系数R₂分别为0.999、0.973和0.943，调整后的决定系数R₂adj分别为0.998、0.962和0.925，可以看出，K和m的响应面模型精度都非常高。

利用连续二次规划优化方法对响应面模型进行优化得到确定性最优解（表6-13）。根据各变量的分布类型和标准差（表6-12），通过蒙特卡罗描述性抽样得到1000组设计变量，将这1000组设计变量代入m、K和f的响应面模型中，可求得响应的均值和标准差，即可判断响应随设计变量波动的敏感度，6σ稳健性优化设计相当于在每一次确定性优化后进行一次稳健性评估。

2.控制结果

经过1000次内循环（6σ稳健性评估）和17次外循环（确定性优化），最终得到稳健性最优解（图6-55和表6-13）。相比初始设计，6σ稳健性最优解下垂刚度提高14.9%，一阶扭转模态性能提高9.6%，车门质量减小1.39kg；相比确定性最优解，6σ稳健性最优解车门质量有所增加，但下垂刚度和一阶扭转模态频率增幅更大且远离约束边界，K和f的标准差σ减小，降低了下垂刚度和一阶扭转模态随变量波动的敏感性，设计变量也远离边界，都达到6σ水平，下垂刚度和一阶扭转模态都达到6σ水平。

图6-55 优化的迭代收敛过程

表6-13 初始值、确定性最优解和稳健性最优解

（续）

稳健性是评价产品质量的重要指标之一。6σ稳健性优化是优化设计结合6σ质量控制准则的一种稳健优化策略。对于拼焊板车门这类比较复杂的系统，其品质受到许多随机因素的影响而很难保证其稳健性。本算例将试验设计、响应面法、优化算法和蒙特卡罗模拟技术相结合，构造了基于6σ稳健性的车门轻量化设计方法。该方法在轻量化设计初期就考虑到各种不确定因素的影响，从而在减轻车门质量的同时，能够较大幅度地提高车门品质的稳健性。对某车门轻量化实例研究表明，基于6σ稳健性的轻量化结果不仅优于初始设计，而且稳健性得到很大提高。