层次分析法(AnalyticHierarchyProcess,简称AHP)是将与决策总是有关的元素分解成目标层、准则层、方案层等层次,在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初,在为美国国防部研究“根据各个工业部门对国家福利的贡献大小而进行电力分配”课题时,应用网络系统理论和多目标综合评价方法,提出的一种层次权重决策分析方法。
层次分析法特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上,利用较少的定量信息使决策的思维过程数学化,从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。尤其适合于对决策结果难于直接准确计量的场合。
层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体的备投方案的顺序分解为不同的层次结构,然后用求解判断矩阵特征向量的办法,求得每一层次的各元素对上一层次某元素的优先权重,最后再加权的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。这里所谓“优先权重”是一种相对的量度,它表明各备择方案在某一特点的评价准则或子目标下优越程度的相对量度,以及各子目标对上一层目标而言重要程度的相对量度。层次分析法比较适合于具有分层交错评价指标的目标系统,而且目标值又难于定量描述的决策问题。其用法是构造判断矩阵,求出其最大特征值。及其所对应的特征向量W,归一化后,即为某一层次指标对于上一层次某相关指标的相对重要性权值。
层次分析法在紧密结合现场实际的基础上,综合考虑影响排采工艺优选的多种技术经济指标,将模糊数学的有关原理,系统地应用于煤层气井排采工艺方法选择的优化决策中。因此,较以往的单因素分析法更为合理。此外,在权重的确定上,综合考虑现场实际和专家意见,应用灰色理论中的灰色关联度法,将模糊数学与灰色理论有机地结合起来,得出的权重结果将更加符合现场实际。
煤层气排采工艺优选决策必须对不同的排采工艺进行技术经济指标分析评价,并结合气井的地质特征、工艺适应性等因素进行综合分析和比较。煤层气排采工艺优选决策程序见图4-48。
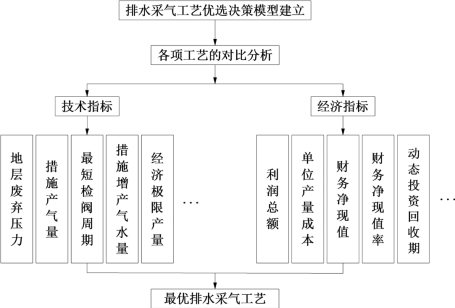
图4-48 排采工艺优选决策程序
煤层气排采工艺优选评价模型建立过程如下。
(1)方案入选,建立复合物元A
物元理论是利用物元模型解决实际问题,既可以利用物元可拓性的物元方法,又可以采用可拓集合理论,通过关联函数进行定量计算。物元理论的基本单位是物元,是以事物、事物特征和该特征的量值三者所组成的三元组,记作R=(事物,特征,量值)。
物元的概念反映了质与量之间的关系,可以更贴切地描述客观事物变化的过程。不同的物体可以有相同的特征元,用同征物元表示。事物变化的可能性称为物元的可拓性。事物的变化以物元的变换来描述,物元理论的核心就是研究物元的可拓性和物元的变换以及物元变换的性质。物元集合的主要内容是定量描述事物的可变性,通过建立关联函数进行计算。
针对目前排水采气工艺的现状,结合现场实际,假设有m个排水采气工艺方法可供选择,每一种方法有n个评价指标,并令第i个排水采气工艺的第j个指标值为aij,则建立的复合物元A为:
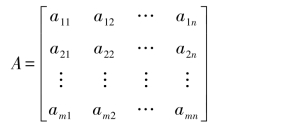
(2)效用函数的计算
利用效用函数法对有量纲的各指标进行归一化处理,其处理方法有:
①希望指标值越大越好,其效用函数的计算为:

②希望指标值越小越好,其效用函数的计算为:
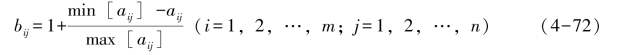
③希望指标以某个值r∗为中值,与r∗越接近越好时,其效用函数的计算为:
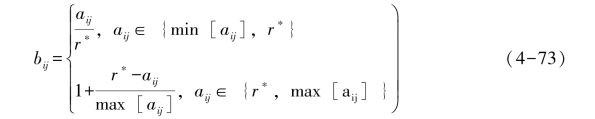
由此可得到效用函数矩阵B:
![]()
(3)指标权重的计算
指标权重值反映各项指标相对重要程度,对于排水采气工艺方案的选择至关重要。指标权重值不同,评价结果也会不同,甚至出现完全相反的结果。AHP层次分析法是对指标体系中的各指标进行两两比较,按照表4-4所给的标度,记下比较结果,例如指标Pi相对于指标Pj的重要性为Pij(如为3或5),则指标Pj相对于指标Pi的重要性为Pji(为1/3或1/5),如此类推,可构造一个判断矩阵:
![]()
由此进行指标权重的计算。判断矩阵标度及含义见表4-4。
表4-4 判断矩阵标度及含义
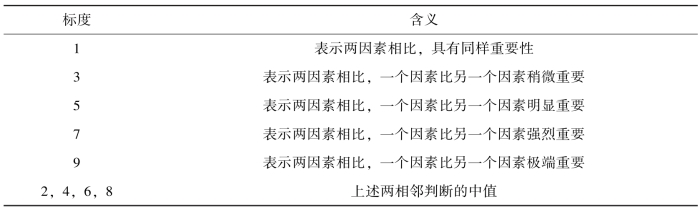
①构造等价矩阵。由于对比矩阵不一定满足判断一致性,为了避免多次调整判断矩阵才能满足一致性要求,利用最优传递矩阵,对对比矩阵进行改良,使之自然满足一致性要求,建立等价矩阵,令:

以![]() 作为判断矩阵与P完全等价,且具有判断一致性。
作为判断矩阵与P完全等价,且具有判断一致性。
②根据已经求得的等价矩阵,用方根法求某元素的权重:
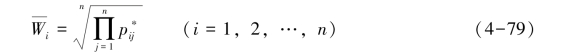
③将Wi规范化:

则W=[W1,W2,…,Wn]T即为该层各有关元素对上一层次中相关某准则的权重。
④计算总权重。若上一层有m个因素,其权重分别为a1,a2,…,am,本层次n个因素A1,A2,…,An对于上层每个因素的相对权重为![]() (i=1,2,…m),则本层每个因素的组合权重为:
(i=1,2,…m),则本层每个因素的组合权重为:
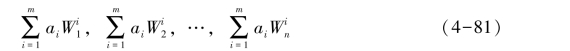
可如此一层一层自上而下求,直至底层所有因素权重均可求出。
(4)模糊决策模型的建立
由上述求出的各指标的权重W=[W1,W2,…,Wn]T和各指标的效用函数Bij,则各方案的综合效用值为:
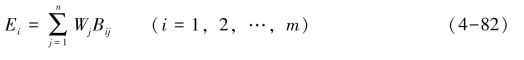
Ei值越大,则方案的技术经济效益越好,故可依据Ei值的大小来进行方案排序,得出排采工艺优选模糊决策模型为:
![]()
层次分析法优势在于该方法把研究对象作为一个系统,按照分解、比较判断、综合的思维方式进行决策,成为继机理分析、统计分析之后发展起来的系统分析的重要工具。系统的思想在于不割断各个因素对结果的影响,而层次分析法中每一层的权重设置最后都会直接或间接影响到结果,而且在每个层次中的每个因素对结果的影响程度都是量化的,非常清晰、明确。这种方法尤其可用于对无结构特性的系统评价以及多目标、多准则、多时期等的系统评价。层次分析法既不单纯追求高深数学,又不片面地注重行为、逻辑、推理,而是把定性方法与定量方法有机地结合起来,使复杂的系统分解,让人的思维过程数学化、系统化,便于人们接受,且能把多目标、多准则又难以全部量化处理的决策问题化为多层次单目标问题,通过两两比较确定同一层次元素相对上一层次元素的数量关系后,最后进行简单的数学运算。层次分析的基本原理很好理解,基本步骤容易掌握,计算也简便,并且所得结果简单明确,容易为决策者了解和掌握。层次分析法主要是从评价者对评价问题的本质、要素的理解出发,比一般的定量方法更讲求定性的分析和判断。由于层次分析法是一种模拟人们决策过程的思维方式的一种方法,层次分析法把判断各要素的相对重要性的步骤留给了大脑,只保留人脑对要素的印象,化为简单的权重进行计算。这种思想能处理许多用传统的最优化技术无法着手的实际问题。(https://www.xing528.com)
层次分析法也存在一定的问题。层次分析法的作用是从备选方案中选择较优者。这个作用正好说明了层次分析法只能从原有方案中进行选取,而不能为决策者提供解决问题的新方案。对科学的方法的评价中,一般都认为一门科学需要比较严格的数学论证和完善的定量方法。但现实世界的问题和人脑考虑问题的过程很多时候并不是能简单地用数字来说明一切。层次分析法是一种带有模拟人脑的决策方式的方法,因此必然带有较多的定性色彩。定性成分较多的时候,可能这个研究最后能解决的问题就比较少。更重要的是,指标过多时数据统计量大,且权重难以确定。当我们希望能解决较普遍的问题时,指标的选取数量很可能也就随之增加。指标的增加就意味着我们要构造层次更深、数量更多、规模更庞大的判断矩阵。那么就需要对许多的指标进行两两比较的工作。由于一般情况下层次分析法的两两比较是用1~9来说明其相对重要性,如果有越来越多的指标,甚至会对层次单排序和总排序的一致性产生影响,使一致性检验不能通过,也就是说,由于客观事物的复杂性或对事物认识的片面性,通过所构造的判断矩阵求出的特征向量(权值)不一定是合理的。还有,就是特征值和特征向量的精确求法比较复杂。
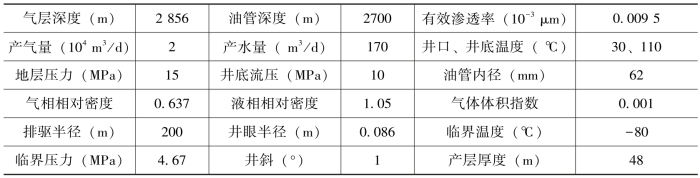
以四川盆地威远气田威23井为例,该井的基本数据见表4-5。考虑气举、有杆泵、电潜泵和射流泵等4项排采工艺技术以供选择。
表4-5 威23井基本数据表
①技术、经济指标预测。对有杆泵等4项排采工艺进行了总产气量、经济极限产量、净现值、利润总额、投资回收期和工艺成本的技术经济指标的预测计算,见表4-6。
表4-6 威23井的基本技术经济指标数据表
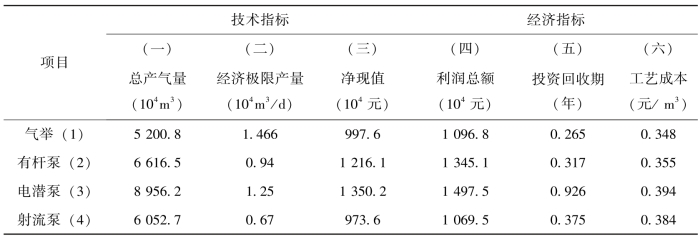
注:年生产时间330d,评价期为8年。
②准则层指标权重的计算。对准则层各项指标进行对比打分,建立判断矩阵,从而计算各层指标的权重。
第一层次(目标层):各项工艺的对比分析。
第二层次(准则层):经济指标和技术指标的权重分析。
P1——技术指标,P2——经济指标,取P12=1/2,P21=2
即
![]()
构造等价矩阵:令cij=lgpij,则
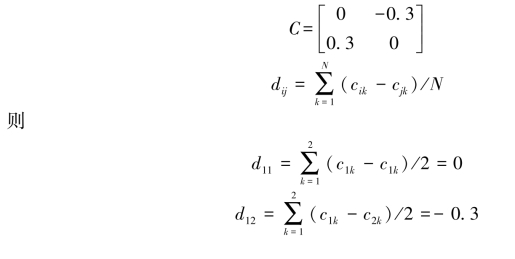
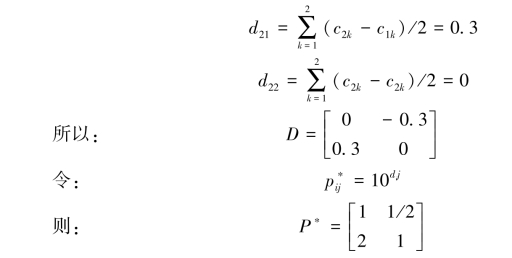
用方根法求得:
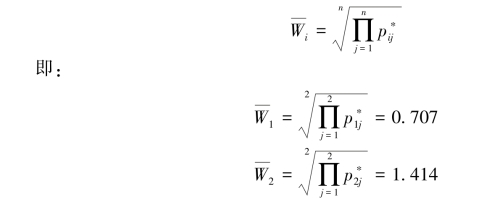
将Wi规范化:
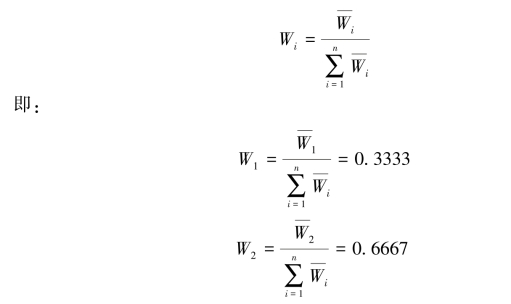
所以,相对于各项工艺而言,经济指标和技术指标的权重分别为0.3333和0.6667,见表4-7。
表4-7 各工艺第二层指标的权重值表

③根据以上各方案具体指标值(表4-8)分别建立技术指标和经济指标的复合物元Amn1和Amn2。
表4-8 技术指标和经济指标
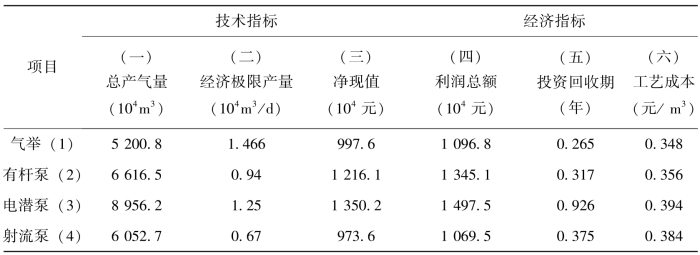
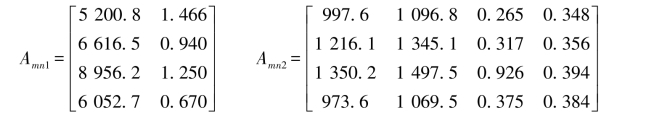
④指标归一化处理,建立效用函数矩阵Bmn1和Bmn2。根据归一化的数学模型,将各指标值处理成为(0,1)之间的值,为各项指标的计算提供基础。第(1)(2)(3)(4)项越大越好,第(5)(6)项越小越好。
效用函数矩阵Bmn:
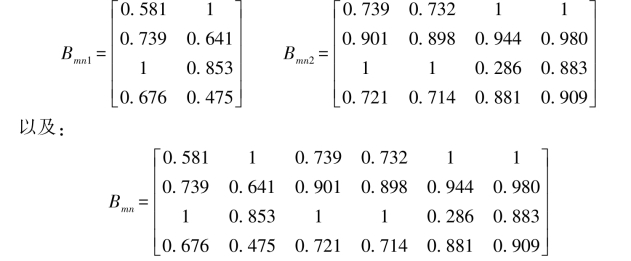
⑤方案层指标权重的计算。
技术指标包括总产气量P1和经济极限产量P2。
取P12=1/3,P21=3
即:
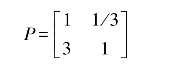
构造等价矩阵,令cij=lgpij,则:
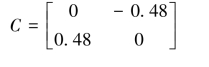

用方根法求得:
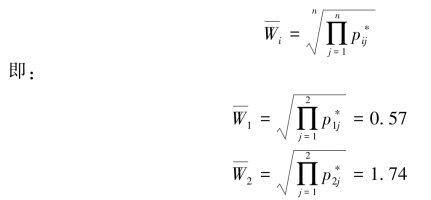
将Wi规范化:
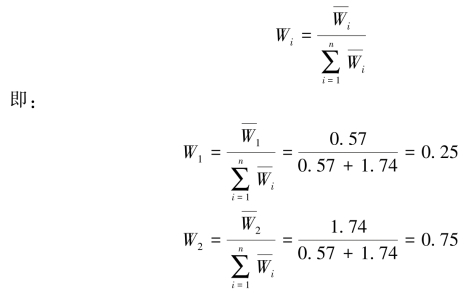
由于技术指标权重为0.3333,则各项技术指标的权重为:
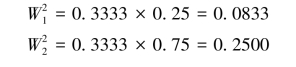
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




