母线平行于z轴的柱面方程解析与点评

1.，故选（A）。

点评：极限运算法则，要熟记两个重要极限。

2.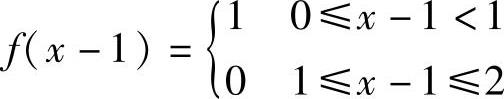，即，故选（B）。

点评：函数关系即是对应关系。

3．，故选(C)。

点评：导数定义一定要清楚。

4.，故选（B）。

点评：复合函数求导法则是求导数的最重要部分，一定要熟练掌握。

5.因。所以，dy与Δx是同阶非等价无穷小，故选（B）。

点评：掌握微分的计算，清楚无穷小比较的概念。

6.两边对x求导数，得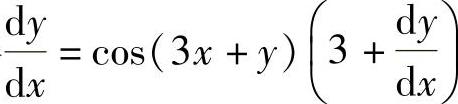，即，故选（D）。

点评：隐函数导数的求法要掌握。

7.y′=-e^2x-2xe^2x，dy|_x=0=-1，切线方程为y-1=-x，即x+y=1选（B）。

点评：清楚导数的几何意义即切线斜率，会求切线方程、法线方程。

8.。故选（B）。

点评：洛必达法则是求极限的重要方法，很多难求的极限用洛必达法则会变得较容易。

9.，x<0，y′<0，函数单调减少，所以单调区间为（-∞，0），故选（C）。

点评：利用导数研究函数的单调性很方便，应记住：导数大于零，函数单调增加；导数小于零，函数单调减少。

10.y′=3x²-6x，y″=6x-6，令y″=0，得x=1。故在x=1的左右出现y″异号，所以拐点为（1，-2），选（A）。

点评：拐点的必要条件是在该点的二阶导数为零。

11.，故选（D）。

点评：注意抽象函数的表示，例如f′（x²）是表示对x²求导，而不是对x的导数。

12.设B点为（x，y，z），，得x-2=2，y-1=1，z-3=4，即x=4，y=2，z=7，选（B）。

点评：已知向量起点与终点的坐标，则向量的坐标是对应两点坐标的差。

13.因向量a与b平行，所以有，得μ=15，，故选（D）。

点评：两个向量平行的充要条件是对应坐标成比例。

14.同时垂直于a、b的向量为a×b=-4i+2j+2k，也符合要求，故选（C）。

点评：应知道向量a×b是同时垂直于a与b的向量。

15.因s与-s都可作为L的方向向量，（A）、（C）都是L的方程，化为参数方程即是（D），（B）表示的不是L的方程，故选（B）。

16.，

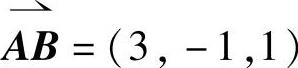平面法向量

平面方程4（x+1）+18（y-1）+6（z-2）=0

可化为2x+9y+3z-13=0，故选（A）。

点评：平面的法向量是写出平面方程的关键。

17.选（D）。

点评：方程中不含z的即是母线平行于z轴的柱面方程。

18.方程可化为x²+（y-2）²+z²=5，为球面的标准方程，故选（B）。

点评：要熟悉球面的标准方程。

19.因平面的法向量与直线的方向向量平行，所以直线与平面垂直，故选（B）。

点评：直线的方向向量与直线平行，平面的法向量与平面垂直。

20.，fx′（x，1）=1，选（B）。

点评：求完偏导数后将某点代入即可求得偏导数在该点的值。

21.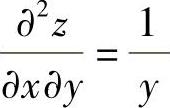，，故选（B）。

点评：二阶偏导数求解是在求完一阶偏导数后再继续求导的过程。

22．，故选（D）。

点评：变上限定积分的导数为。

23.f′（x）=x²（x-1）（x-2），令f′（x）=0，得驻点0，1，2。0点左右f′（x）符号相同，1、2为极值点，故选（C）。

点评：极值点的必要条件是在该点的导数为零。

24.，选（C）。

点评：被积函数为奇函数时在对称区间积分为零，例如上面的第一个积分。后一个可利用定积分的几何意义，即此积分正好是半圆的面积。

25.f（x）=（xsinx）′=sinx+xcosx

∫xf′（x）dx=∫xdf（x）=xf（x）-∫f（x）dx

=x（sinx+xcosx）-xsinx+C=x²cosx+C，故选（B）。

点评：清楚原函数的概念，分部积分法是求积分的主要方法之一。

26.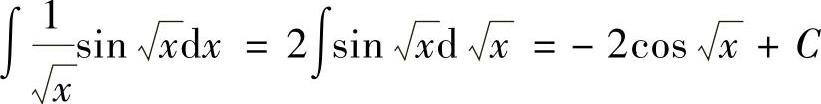，故选（C）。

点评：第一换元积分法是求积分最常用的方法。

27.，故选（A）。

点评：同上。

28.，故选（D）。

点评：掌握定积分的分部积分法在求解中的应用。

29.，故选（B）。

点评：积分限上是x的函数时，求导数的一般情形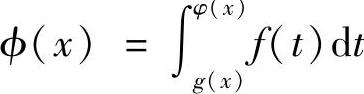，，则ϕ′（x）=φ′（x）f[φ（x）]-g′（x）f[g（x）]。

30.由得两交点（0，0）、（2，4），所围面积，故选（D）。

点评：利用定积分求面积是定积分的一项重要应用。

31.所求体积为，故选（D）。

点评：利用定积分可求旋转体体积。

32.，选（B）。

点评：第二类换元积分法与分部积分法可同时用来求定积分。

33.选（A）。

点评：可以借助于图形来完成。

34.，选（D）。

点评：利用直角坐标计算二重积分。

35.，故选（A）。

点评：当二重积分区域与圆有关时，用极坐标计算可能更简单。

36.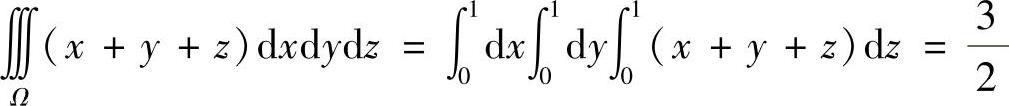，选（C）。

点评：要掌握三重积分的计算。

37.，故选（C）。

点评：要掌握广义积分的计算方法。

38.，选（A）。

点评：要掌握对坐标的曲线积分，方法是将曲线方程带入被积表达式后化为定积分。

39.，选（D）。

点评：同上题。

40.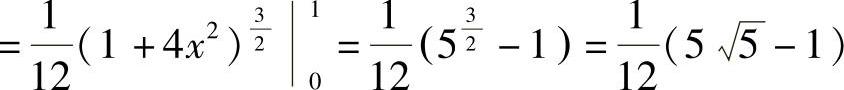，故选（B）。

点评：对弧长的曲线积分要掌握方法。当曲线方程为y=f（x）时，ds=1+[f′（x）]²dx。

41.选（B）。

点评：要知道级数收敛的必要条件是一般项的极限为零。

42.选（D）。因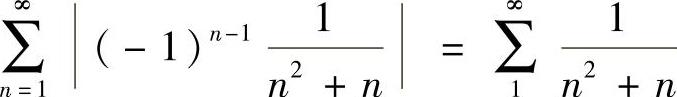，故收敛。

点评：要清楚绝对收敛与条件收敛的概念。

43.选（C）。因，由，知级数收敛，且发散。

点评：要掌握交错级数的莱布尼茨收敛法。

44.选（A）。因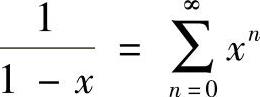，所以。

点评：应记住展开式。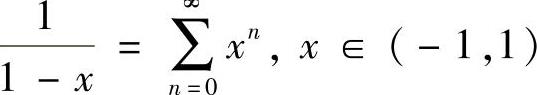

45.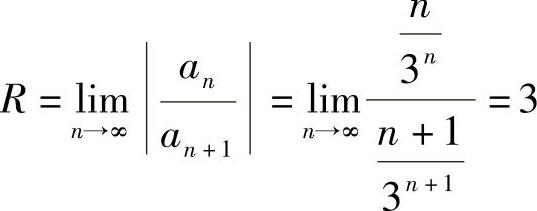，故选（C）。

点评：要掌握求幂级数收敛半径的方法。

46.由上题方法可求得R=1，知在（0，2）上级数收敛，当x=0时，级数发散；当x=2时，级数收敛。所以收敛域为（0，2]，故选（D）。

点评：求幂级数收敛域时，端点要代入单独讨论。

47.，，故选（A）。

点评：学会用间接展开法将函数展开为幂级数，并要牢记几个常用的展开式。

48.π是f（x）的间断点，f（x）的傅里叶级数应收敛于，故选（D）。

点评：要记住狄里克莱收敛定理。

49.分离变量后原方程为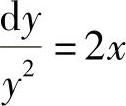，两端积分得，故选（B）。

点评：掌握可分离变量微分方程的解法。(www.xing528.com)

50.令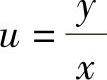，则，代入原方程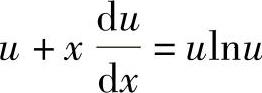，，分离变量，积分ln（lnu-1）=lnx+lnC，得lnu-1=Cx，将代回，得，故选（C）。

点评：齐次方程的求解，令可化为可分离变量方程。

51.积分一次为，再积分得，故选（A）。

点评：这种可降阶的微分方程，通过积分即可求得它的解。

52.通解，由y|_x=π=1，得C=π-1，即，故选（C）。

点评：求一阶线性微分方程的解可直接用公式。

53.特征方程r²-2r-3=0的根为r₁=-1，r₂=3，通解为y=C₁e^-x+C₂e^3x，故选（A）。

点评：二阶常系数线性齐次微分方程的通解可由特征方程根的三种不同情形写出。

54.特征方程r²+6r+13=0的根为r_1，2=-3±2i，通解为y=e^-3x（C₁cos2x+C₂sin2x），故选（B）。

55.特征方程r²+2r+1=0的根为r_1，2=-1，通解为y=e^-x（C₁x+C₂），故选（C）。

56.，故选（D）。

点评：要掌握行列式的性质。

57.（A-I）²=（A-I）（A-I）=A²-AI-IA+I²=A²-2A+I，故选（D）。

点评：矩阵与矩阵的乘法不满足交换律，单位矩阵I与任何矩阵相乘还等于该矩阵。

58.，故选（B）。

点评：要清楚A^-1与A^∗的关系，即A^∗=|A|A^-1。

59.，第二行第二列为0，故选（A）。

点评：考查逆阵的性质。

60.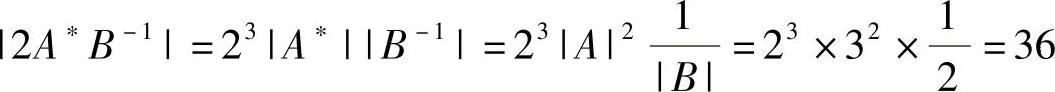，选（D）。

点评：注意n阶矩阵A，。

61.因AB是m×m矩阵，BA是n×n矩阵，r（BA）≤min{r（A），r（B）}≤m<n，所以|BA|=0，选（C）。

点评：注意矩阵秩的若干结论，如r（AB）≤min{r（A），r（B）}，r（A_n×m）≤min{m，n}，r（A_n×n）=n等价于|A|≠0。

62．,

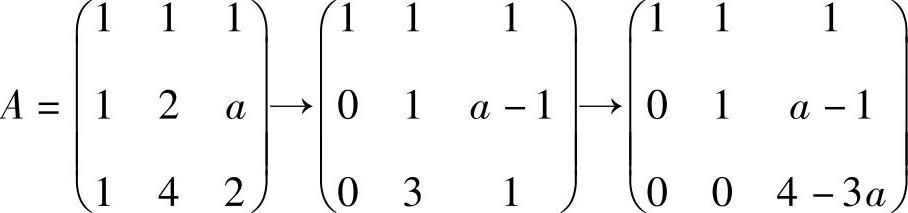因r（A）=2，所以4-3a=0，得，故选（B）。

点评：应掌握用初等变换求矩阵秩的方法。

63.第二行各元素与第四行对应元素的代数余子式乘积之和应为零，即2A₄₁+2A₄₂+2A₄₃+2A₄₄=0，所以有2（A₄₁+A₄₂+A₄₃+A₄₄）=0，得A₄₁+A₄₂+A₄₃+A₄₄=0，故选（A）。

点评：行列式某行各元素与另一行对应元素的代数余子式乘积之和为零。

64．'因向量组线性无关，秩应小于3，即（t+3）（t-1）=0，得t=-3或t=1，故选（D）。

点评：矩阵的秩等于它的列（行）向量组的秩。

65.显然α₁、α₂线性无关，α₃可由α₁、α₂线性表示，则α₁、α₂、α₃线性相关，秩应为2。

应有t-1=0，即t=1，故选（B）。

点评：向量组α₁，α₂，…，α_m线性相关的充要条件是向量组中至少有一个向量可由其他向量线性表示。

66.选（C）。

点评：齐次线性方程组Ax=0有非零解的充要条件是A的列向量组线性相关。

67.因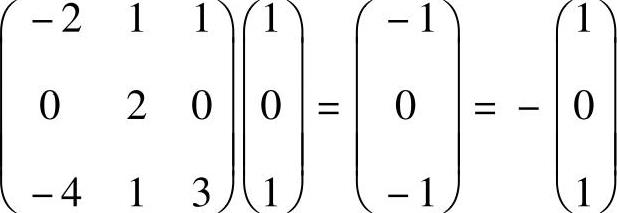，故选（B）。

点评：应清楚矩阵特征值与特征向量的关系。

68．

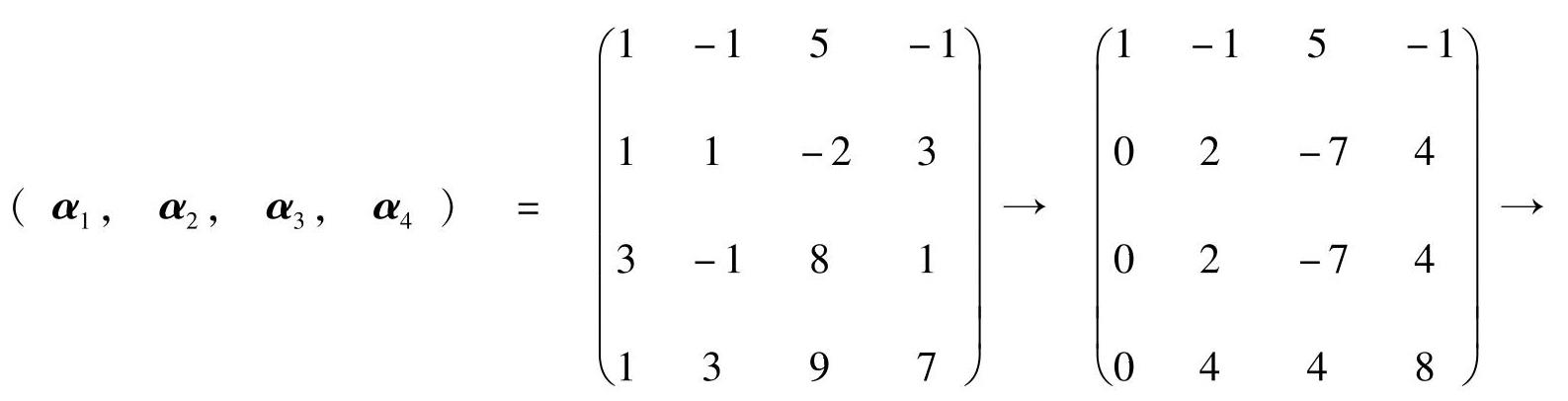
得秩为3，且α₁、α₂、α₃为一个极大线性无关组，故选（C）。

点评：应掌握用初等变换求极大线性无关组的方法。

69.增广矩阵，

因方程组有解，系数矩阵秩为2，应与增广矩阵的秩相等，所以a=2，故选（B）。

点评：非齐次线性方程组有解的充要条件是系数矩阵的秩等于增广矩阵的秩。

70.，应有6-4k=0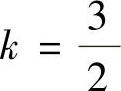，，故选（D）。

点评：齐次线性方程组有非零解的充要条件是系数矩阵的秩小于未知量个数。

71.因k₁α₁+k₂α₂是Ax=0的通解，是Ax=b的特解，故应是Ax=b的通解，故选（C）。

点评：应清楚线性方程组通解的结构，齐次方程组的通解加非齐次方程组的特解应为非齐次方程组的通解。

72.因|A|=1×2×3=6，，故选（B）。

点评：考查特征值的性质，n阶方阵A的特征值为λ₁、λ₂、…、λ_n，则|A|=λ₁λ₂…λ_n。

73.由题目中所给三个式子可知，A的特征值为1、2、-3，所以|A|=1×2×（-3）=-6，故选（D）。

点评：A的特征方程|A-λI|=0的根即为A的特征值。

74.选（B）。

点评：本题考查初等变换的性质。

75.，A的特征值为0、0、0、8，故选（D）。

点评：应掌握矩阵特征值求法。

76.选（B）。

点评：应知道矩阵不同的特征值对应的特征向量是线性无关的。

77.A的特征值是1、2、3，则A²+A的特征值为1²+1=2，2²+2=6，3²+3=12，所以|A²+A|=2×6×12=144，故选（D）。

78.选（C）。

点评：A与B相似，则它们的特征多项式相同、特征值相同、行列式相同，且|A^T|=|B^T|。

79.A是正定矩阵，故各阶主子式应大于零。因1、2阶主子式都是大于零的，得，故选（D）。

点评：A是正定矩阵的充要条件是：A的各阶主子式大于零。

80.选（C）。

点评：若x是A的对应于特征值λ的特征向量，则kx（k≠0）也是λ对应的特征向量。

81.所求概率应为，故选（C）。

点评：考查古典概率的求法。

82.因A与B互为对立事件，所以B发生A一定不发生，故AB=Ø，A∪B=Ω，所以（B）、（C）、（D）都正确，（A）不正确，故选（A）。

点评：正确理解对立事件的概念。

83.P（X=2）=C²₅p²（1-p）³，故选（A）。

点评：考查二项分布。

84.由，得A=4，故选（B）。

点评：考查概率密度的性质。

85.x<0时，F（x）=0；0≤x≤1时，；x>1时，，故选（B）。

点评：清楚分布函数与密度函数的关系。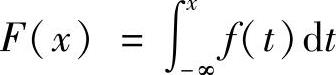

86.由，得A=3，故选（C）。

点评：清楚联合密度函数的性质。

87.x≤0时，；x>0时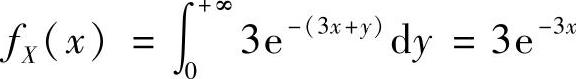，，故选（A）。

点评：考查。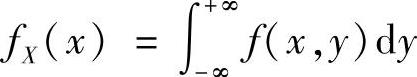

88.E（2X+Y）=2E（X）+E（Y）=2×5×0.2-1=1，故选（D）。

点评：考查数学期望的性质。

89.D（2X-Y）=2²D（X）+D（Y）=2×2×4+9=25，故选（C）。

点评：考查方差的性质。

90.由条件知D（X）=E（X²）-E²（X）=4，D（Y）=9，

D（X+Y）=D（X）+D（Y）+2Cov（X，Y）=4+9+2×1.2=15.4，故选（D）。

点评：清楚协方差与相关系数的关系。

91.选（C）。

点评：考查不相关的概念。独立与不相关的关系：独立一定不相关，不相关不一定独立。

92．'',

由P（X=1，Y=1）=P（X=1）P（Y=1），得，

由P（X=1，Y=2）=P（X=1）P（Y=2），得，

解得，，故选（B）。

点评：考查独立概念和边缘分布律的求法。

93.

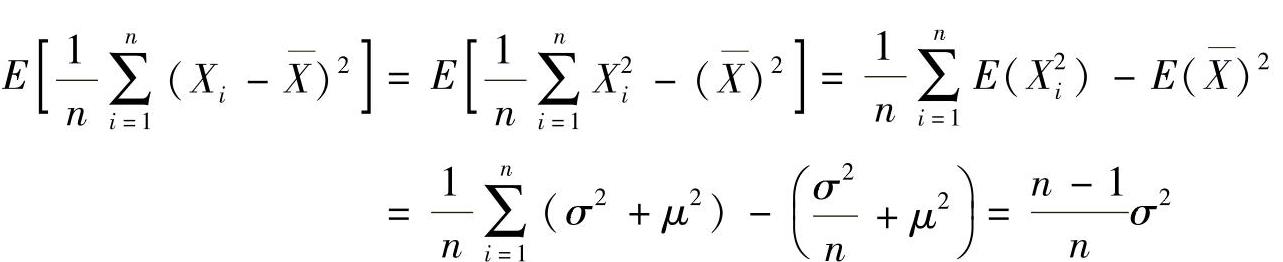
两边同乘得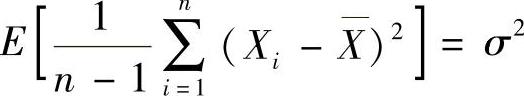：，故选（C）。

点评：考查无偏估计量的概念。应记住样本均值是总体均值的无偏估计量，样本方差是总体方差的无偏估计量。

94.选（D）。

点评：统计量是不含未知参数的样本的函数。

95.选（B）。

点评：考查χ²（n）分布的定义。

96.由F（x，-∞）=0，F（-∞，y）=0，F（+∞，+∞）=1，，

点评：考查联合分布函数的性质。