3-1.《营造法式》的材份制度
材份制度为古代建筑设计和施工中所依据的模数制度，在《营造法式》中得到了详细的阐述和说明（表3-5-3）。
表3-5-2 令栱构件数据表（剔除特异值后） （单位：毫米）
1CV值为标准差同平均数之比，用于进行不同类型样本之间的稳定性比较。
表3-5-3 《营造法式》材份规定值
有关一些基本数值间的比例关系，《营造法式》卷四《材》中规定：“栔广六分，厚四分。材上加栔者谓之足材……各以其材之广，分为十五分，以十分为其厚。”则可以得出，根据法式规定：
关于材份制的用途，《营造法式》卷四《材》中有明确的说明：“凡构屋之制，皆以材为祖；材有八等，度屋之大小，因而用之……凡屋宇之高深，名物之短长，曲直举折之势，规矩绳墨之宜，皆所用材之份，以为制度焉。”
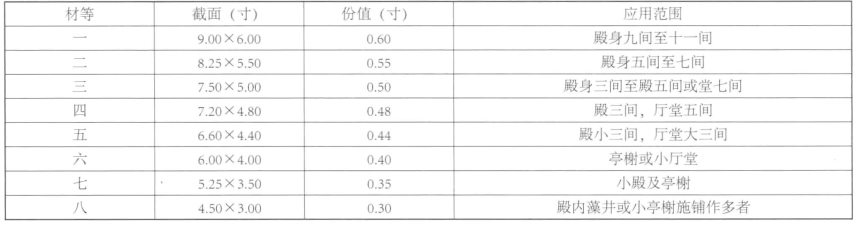
可见，材份制在《营造法式》中规定首先被用于“度屋之大小”，即根据不同房屋规模和等级的需要，进行不同的材等取值，其具体规定如表3-5-4。
《营造法式》中还规定材份用于“名物之短长”，这主要体现在《营造法式》卷四、卷五对于建筑大木作各个部分和各种构件设计和施工尺寸的份数规定，包括斗棋构件中的斗、栱、昂、耍头、替木等构件尺寸，以及柱梁构件中柱、梁栿、叉手、阑额、槫、椽、蜀柱等构件尺寸。
表3-5-4 《营造法式》材等使用范围规定
(www.xing528.com)
表3-5-5 《营造法式》规定广为一材的大木作构件表
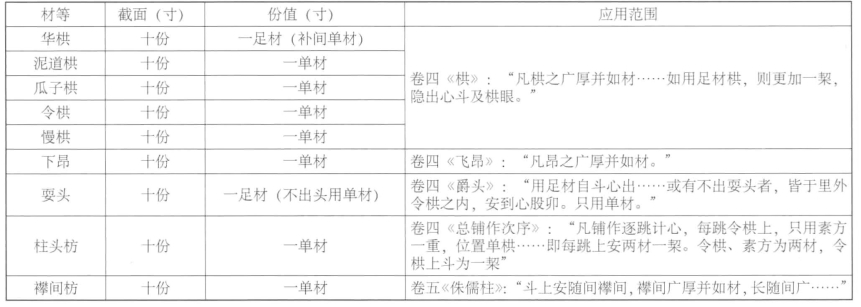
根据上文，对大殿进行大木尺度分析从斗栱和柱梁构件中的细部数据入手，对大殿材等和营造用尺进行同时复原。据《营造法式》可知，材厚是通过材广定义的，在进行材等和营造尺复原过程中，应用材广数值作为计算和分析的自变量。因此，选取《营造法式》中规定高度为一材的构件数据作为复原的样本，具体见表3-5-5。
结合稷王庙大殿实际情况，就稷王庙大殿外檐斗棋构件而言，高度为一材的构件有泥道棋、泥道慢栱（隐刻）、泥道第三层枋，泥道第四层棋、华栱、耍头、襻间枋等。以列为9个此类构件进行数据处理后所得的材高数值。
表3-5-6 稷王庙大殿高为一材构件材高数值表 （单位：毫米）
表3-5-7 构件总体平均值一致性检验
由表3-5-6可见，根据《营造法式》规定所见稷王庙大殿外檐铺作高度为一材的这9类构件，其数据处理所得单材高平均值并非一致，因此需要对其总体平均值的一致性进行检验。由于这十类构件测量样本数均小于30，属于互相独立的小样本，在对其平均值一致性检验时采用t检验的方法，即认为当两个统计量本身样本数据服从正态分布时，且其方差差别不大时，两个平均值的差值经标准化
后，服从自由度为（n1+n2-2）的t分布函数。
通过t函数表可以得到不同自由度的t函数的累积概率值。也就是说，给定显著性水平α，可以查到不同自由度情况下的临界值tα，使得t≥tα的概率等于α，即P｛t≥tα｝=α。[14]
观察上述9类构件，此9类构件的原始数据基本服从正态分布规律，但就标准差来看，泥道第三层枋和补间里转第二跳华棋的测量值标准差明显大于其他构件，因此不具备和其他构件进行t检验的条件，所以在进行总体平均值一致性检验时将这两类构件舍去。
表3-5-7为针对7类构件两两进行总体平均值t检验所得的累计概率值，本文以0.01作为判定标准认为两构件组合具有平均值的一致性。
如表3-5-7所示，在设定的概率判定标准下，每一类构件均同其他构件有在至少一组的情况下存在总体平均值一致的情况，因此不能贸然认为某一类构件的单材高度所用设计值同其他不同，因此，在进行材等和营造尺复原的过程中，采用大殿外檐铺作泥道栱（包括泥道第一层棋和泥道第四层栱）、泥道慢栱（第二层柱头枋）、令栱、华栱（第一跳华栱）、耍头以及下平槫襻间枋这7类构件作为样本。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
