隧道工程中的数值法及范围选取

通常情况下，隧道结构几何形状复杂，围岩具有各种不同的非线性特性；而且衬砌支护结构的计算还与开挖方法、支护过程等有关。对于这类复杂问题，一般需要采取数值分析方法加以解决。

常用的数值方法有有限单元法、边界元法和离散元法等，其中有限元法和边界元法建立在连续介质力学的基础上，适合小变形分析，是发展较早、较成熟的方法，尤其以有限元法应用更为广泛，目前它已成为隧道工程围岩稳定性分析和支护结构强度计算的有力工具。它把围岩和支护结构都划分为若干单元，然后根据能量原理建立单元刚度矩阵，并形成整个系统的总刚度矩阵，从而求出系统中各节点的位移和单元的应力。以下以平面应变问题（隧道工程可按平面应变问题简化处理）来说明有限元解法的一般过程。

1．单元类型的选择和网格划分

对平面应变问题常采用的有限单元包括线单元和面单元，如图6-4-7所示。对于地下结构体系离散化后往往是各种类型单元的组合：二节点和三节点杆单元可用以模拟锚杆；二节点和三节点梁单元可用以模拟喷射混凝土；三节点和六节点三角形常应变单元或四节点、八节点四边形等参数单元用以模拟围岩和二次衬砌。

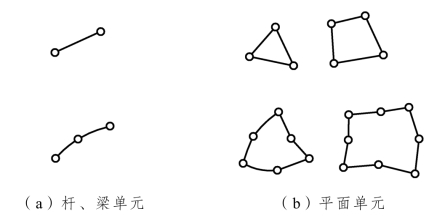
图6-4-7　有限单元的基本类型

通常认为，采用四节点或八节点的四边形等参元模拟围岩最为适宜，因它能适应曲边形的外形，便于进行网格自动划分，也具有较高的计算精度。

支护结构如为喷射混凝土层或整体浇筑的混凝土衬砌，通常都采用与围岩相同的单元类型，这样支护结构单元与围岩单元就可以直接相联，程序处理大为简化。如采用承受轴力的直梁单元来模拟支护结构，其优点是可以直接计算出支护结构的轴力、弯矩和剪力，这对于按规范对支护结构的强度进行校核是很方便的。但梁单元的节点位移矢量中有一个是转角，故不能和平面单元的节点位移相协调，需做特殊处理，如在其间加一个杆单元（模拟回填层），才能和平面单元相联。

对于锚杆的模拟问题，目前最常用的是轴力杆单元，将杆单元的节点与围岩单元的节点牢固相联，变形后也不脱开，即杆单元节点与相应围岩单元节点变形协调。计算实践证明，这种模拟方式不能很好地反映锚杆加固岩体的实际作用效果，只能认为是一种简略的近似计算。许多学者根据锚杆的不同作用效应提出了一些改进的锚杆模拟计算模型，但都没有得到进一步的推广应用。

单元划分的大小、形状和疏密程度也会影响计算的精度，一般来说，单元划分得越密越小、形状越规则，计算精度越高。根据误差分析，应力的误差与单元尺寸的一次方成正比，位移的误差与单元的二次方成正比。但单元数多则要求计算机储存量大，计算时间长。在地下结构物周围区域、地质构造区域等应力、位移变化梯度大以及荷载有突变的区域，单元划分可加密，而其他区域则可稀疏一些。疏密区单元大小相差不宜过大，应尽可能均匀过渡。在结构体系离散化时需注意以下几点：

（1）单元的边长相差不能过大，两边夹角不能过小，各夹角最好尽量相等。

（2）单元边界应当划分在材料的分界面上和开挖的分界线上，一个单元不能包含两种材料。

（3）集中荷载作用点、荷载突变处及锚杆的端点处必须布置节点。

（4）地下结构和岩体结构在几何形状和材料特性方面都具有对称性时，可利用该对称性取部分计算范围进行离散，见图6-4-8。

（5）单元的划分要考虑到分部开挖的分界线和开挖区域的分界线。

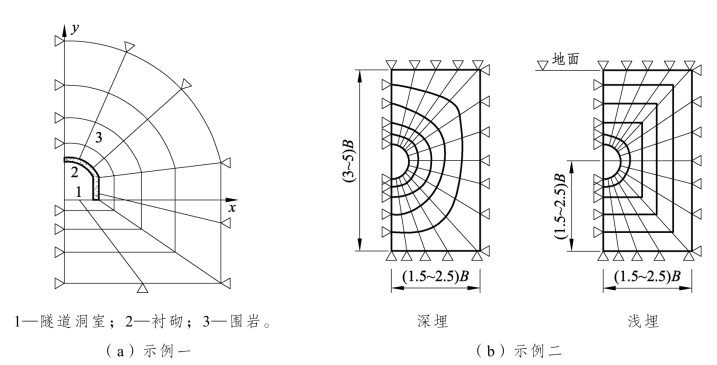
图6-4-8　隧道计算范围及网格划分示例

2．计算范围的选取

有限单元法分析必须是在有限的区域内进行，不可能把分析的范围取为无限大。在岩体中开挖隧道，应力重分布的范围也是有限的，因而计算的范围可取为有限的。确定计算边界时，一方面要节省计算费用，另一方面也要满足精度要求。实践和理论分析表明，对于隧道开挖后的应力应变，仅在洞室周围距洞室中心点3～5倍隧道开挖宽度（或高度）的范围内存在实际变化。在3倍跨度处的应力变化一般在10% 以下，在5倍跨度处一般在3%以下。所以计算边界即可确定为3～5倍开挖宽度（高度）。在这个边界上，可以认为开挖引起的位移为零。此外，根据对称性的特点，分析区域可以取1/2（1条对称轴）或1/4（2条对称轴），如图6-4-8所示。

当要求计算精度增高时，计算边界的确定就比较困难，可考虑采用有限元和无限元耦合算法。

3．边界条件和初始应力

计算范围的边界可采用两种方式处理：其一为位移边界条件，即一般假定边界点位移为零；其二是假定为力边界条件，由岩体的初始应力场确定，包括自由边界（p=0）条件。还可以给定混合边界条件，即节点的一个自由度给定位移，另一个自由度给定节点力（二维问题），如图6-4-9所示。当然，无论哪种处理都有一定的误差，且随计算范围的减小而增大，靠近边界处误差最大，即“边界效应”。边界效应在动力分析中影响更为显著，需妥善处理。

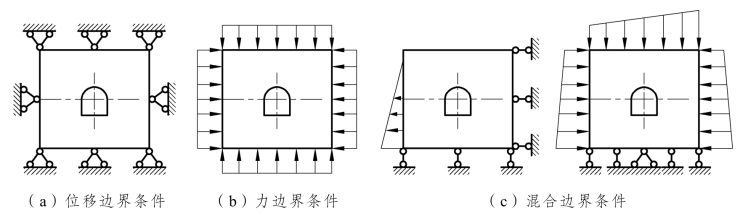
图6-4-9　计算边界的类型

根据以上分析，所取岩体边界上的位移边界条件通常为两侧边界按水平方向固定、铅直方向自由，下边界约束情况一般按铅直方向固定、水平方向自由，如图6-4-10所示。(www.xing528.com)

作用在边界上的初始地应力通常这样考虑：当上部覆盖层厚度不大时，上边界以地面线为自由边界，考虑重力作用，两侧施加三角形分布荷载，侧压系数采用μ/(1-μ)（μ为岩体的泊松比）；当覆盖层很厚时，初始地应力以均布表示，侧压系数以实测或经验确定。

4．卸荷释放荷载及卸荷过程模拟

图6-4-10　边界约束示意图

岩体在开挖隧道之前处于一定的初始应力状态，开挖使隧道周边上各点的应力“解除”，从而引起围岩应力场的变化。如果在开挖的同时设置了支护结构并与围岩密贴，则支护结构将约束围岩因应力场变化而产生的位移，支护结构中也将产生应力和位移。所以，在进行有限元分析时，必须设法模拟这个开挖卸荷的效果。通用的方法就是在隧道周边的点上加“等效释放荷载”。显然，这些“等效释放荷载”是由于隧道周边各点的应力“解除”而形成的，因此，可以根据沿预定周边上的初始应力来确定。

设沿预计开挖边界上各点的初始应力为已知，在离散化的情况下，可假定沿开挖面上两相邻节点之间的初始应力呈线性变化，对于任一开挖边界点，开挖引起的“等效释放荷载”（等效节点力）即可按简支梁分配的原则进行置换。

5．开挖施工步骤的模拟

隧道施工的每一开挖步在力学上都可以认为是一个应力释放和回弹变形问题。为了模拟开挖效应，求得开挖洞室后围岩中的应力状态，可以将每一开挖步开挖释放掉的应力作为等效荷载加在隧道洞室的周边上。开挖施工步骤的模拟方法如下：

（1）按照施工要求划分好开挖顺序，如图6-4-11所示。

（2）按照隧道埋深的地质构造特点，进行开挖前的应力分析，求出围岩中的初始地应力场{σ}0和位移场{δ}0，开挖前的应力状态可作为原始数据直接输入。

（3）根据每次开挖的尺寸，去掉被开挖的单元，根据去掉单元时的应力值，求出被开挖出的自由表面各节点处由这些单元作用的节点力，将与这些节点力大小相等、方向相反的力{P}作用于自由表面相同的节点上，这些力{P}就是等效开挖释放荷载。

（4）在等效开挖释放荷载作用下进行分析，求出该开挖步骤后围岩中的位移{Δδn}、应变{Δεn}、应力{Δσn}，并叠加于以前的状态上。

重复以上步骤，直至最后一个开挖步骤结束。

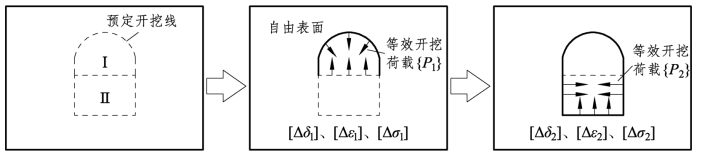
图6-4-11　施工开挖模拟

6．求单元应力

单元刚度矩阵和“释放荷载”的等效节点力求出后，便可按位移法的一般顺序进行求解：组集系统的总刚度矩阵，进行约束位移的处理，解方程求出未知的节点位移，然后根据有限元法的一般理论求算单元应力。

7．围岩与支护结构稳定性判断

根据数值分析计算结果，如何合理地判断围岩的稳定性也是当前尚未解决的一个问题。在数值分析方法中，除非将支护结构离散为梁单元，否则都只能求得支护结构中的应力，因而不能直接采用规范中的公式，即式（6-3-6）、式（6-3-7）等校核支护结构的强度。目前采用的判断围岩与支护结构稳定性的方法主要有如下几种：

（1）超载系数法。将外荷载乘以系数K值，并逐渐增大K值进行反复计算，直到计算不能收敛为止，即认为围岩失稳，K值为安全系数。

（2）材料安全储备法。将材料的主要强度特征值（如c φ、）乘以K值，逐渐降低K值并反复计算到围岩失稳（即计算不收敛）为止，1/K就是安全度。

（3）经验类比法。将计算所得洞壁变形值或塑性区范围与按经验所得的围岩失稳时的允许位移值（极限位移值）或允许的塑性区大小进行比较，由此确定围岩稳定性的安全度。

显而易见。上述各种计算方法所得的安全度是不一样的，并且都缺乏严格的理论依据，这些准则都有待进一步完善。

8．本构关系的选择

弹性（线性或非线性）、塑性和黏性是支护结构和岩土材料的三种基本应力-应变特性。在线性假定下，弹性表示应力与应变呈线性、可逆关系，黏性表示应力与应变速率呈线性关系，塑性表示（当应力超过材料的屈服极限时）应力与应变呈不可逆（即与荷载路径有关）的非线性关系。材料的弹塑性本构模型具有三个组成部分——屈服（超越弹性极限）准则、流动法则和硬化（软化）规则，分别描述材料的破坏机制和条件、应力与塑性应变增量的关系和屈服后材料应变硬化（或软化）的规律。最简单的弹塑性本构模型是理想弹塑性模型，最简单的屈服理论是朗肯的最大应力准则和圣维南（Saint Venant）的最大应变准则，而对于岩土材料，最常用的屈服准则有莫尔-库仑准则和德鲁克-普拉格（Drucker-Prager）准则，在分析时应根据具体情况选用。