隧道工程-隧道支护计算方法

隧道支护结构计算的主要内容有：按工程类比方法初步拟定断面的几何尺寸；确定作用在结构上的荷载，进行力学计算，求出截面的内力（弯矩M和轴向力N）；检算截面的承载力。

目前，隧道支护结构计算采用的荷载-结构模式，主要是在主动荷载及被动荷载（弹性抗力）共同作用下的拱式结构。衬砌结构在主动荷载作用产生的弹性抗力的大小和分布形态取决于衬砌结构的变形，而衬砌结构的变形又和弹性抗力有关，所以衬砌结构的计算是一个非线性问题，必须采用迭代解法或某些线性化的假定。例如，假设弹性抗力的分布形状为已知，或采用弹性地基梁的理论，或用弹性支承代替弹性抗力等等。于是，支护结构内力分析的问题，就成了通常的超静定结构求解。

由于对弹性抗力的处理方法不同，而有几种不同的计算方法，下面分别加以介绍。

1．假定抗力区范围及抗力分布规律法（简称“假定抗力图形法”）

如果经过多次计算和经验积累，基本上掌握了某种断面形式的衬砌在某种荷载作用下的变形规律，以后再计算同类荷载作用下的同类衬砌结构时，就可假定衬砌结构周边抗力分布的范围及抗力区各点抗力变化的图形，只要知道某一特定点的弹性抗力，就可求出其他各点的弹性抗力值。这样，在求出作用在衬砌结构上的荷载后，其内力分析也就变成了通常的超静定结构问题。这种方法适用于曲墙式衬砌和直墙式衬砌的拱圈计算。

图6-3-4为曲墙式衬砌结构采用“假定抗力图形法”求解衬砌截面内力的计算图式。它是一个在主动荷载（垂直荷载大于侧向荷载）及弹性抗力的共同作用下，支承在弹性地基上的无铰高拱。拱两侧的弹性抗力按二次抛物线分布，其量值用三个特征点控制：抗力上零点b，一般与对称中线的夹角为φb，且φb=40°～60°，其精确位置需用逐次逼近法确定；下零点a，在曲墙墙脚处，由于墙脚和围岩间摩擦力很大，故此处无水平位移，因而无弹性抗力；最大抗力点h假设在衬砌跨度最大处，通常h点在抗力区2/3处。

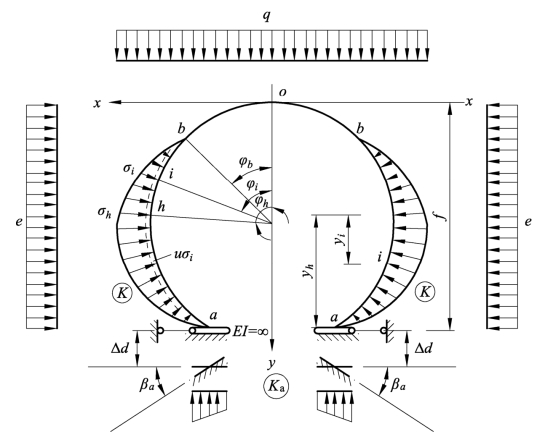
图6-3-4　曲墙式隧道围岩抗力及分布

只要知道特定点，即最大抗力点h（最大跨度处）截面的弹性抗力值，其他各截面的弹性抗力值即可通过与h点弹性抗力值有关的函数关系式求出。因此关键在于不但要求结构内力，还要求h点的抗力值。但是h点的抗力按温氏假定与h点的衬砌变形有关，而该点的变形又是在外荷载和抗力共同作用下得到的，表面上看似乎问题很难求解；实际只是多出h点的一个未知的抗力值，其他问题与拱结构求解没有什么区别，而h点的抗力可以由该点的变形协调条件来求解，即h点的衬砌变形与该点的地层变形是一致的，故最大抗力点的未知数可以多列出一个方程来求解。

最大抗力σh的求解用叠加原理来实现。首先求出在主动荷载作用下衬砌内各截面处的内力MiP、NiP，并求出最大抗力点处的位移δhP；然后再求出σh=1时衬砌结构各截面处的Miσ、Niσ以及h点的变位δhσ；最后利用叠加原理，求得h点的总位移

根据局部变形理论，假设衬砌变形和围岩之间符合文克勒假定，则对于h点，有关系式（6-3-3）：

式中　K——围岩的弹性抗力系数。

将式（6-3-2）代入上式，求得

2．弹性地基梁法

这种方法是将衬砌结构看成置于弹性地基上的曲梁或直梁。弹性地基上抗力按文克勒假定的局部变形理论求解。当曲墙的曲率是常数或为直墙时，可采用初参数法求解结构内力。一般直墙式衬砌的直边墙利用此法求解。

直墙式衬砌的拱圈和边墙分开计算。拱圈为一个弹性固定在边墙顶上的无铰平拱，边墙为一个置于弹性地基上的直梁，计算时先根据其换算长度，确定是长梁、短梁或刚性梁，然后按照初参数方法来计算墙顶截面的位移及边墙各截面的内力值。计算图式如图6-3-5所示。

3．弹性支承法

图6-3-5　直墙式弹性地基梁计算图式

目前，对隧道支护结构计算采用得比较多的方法是弹性支承法。弹性支承法也称为链杆法，其基本特点是将支护结构离散为有限个杆系单元体，按照“局部变形”理论考虑支护结构与围岩的相互作用，将弹性反力作用范围内（一般先假定拱顶90°～120° 范围为脱离区）的连续围岩，离散成若干条彼此互不相关的矩形岩柱。矩形岩柱的一个边长是支护结构的纵向计算宽度，通常取单位长度，另一边长是两个相邻的支护结构单元的长度之半的和。因岩柱的深度与传递轴力无关，故不予考虑。

为了便于计算，用一些具有一定弹性的支承来代替岩柱，并以铰接的方式支承在支护结构单元之间的节点上，使它不承受弯矩，只承受轴力。弹性支承的设置方向应该和弹性反力的方向一致。可以是径向的，不计支护结构与围岩间的摩擦力，如图6-3-6（a）所示，且只传递轴向压力（由于围岩与支护结构存在黏结力，也可能传递少量轴向拉力）；也可以和径向偏转一个角度，考虑支护结构与围岩间的摩擦力，如图6-3-6（b）所示；为了简化计算也可将弹性支承水平设置，如图6-3-6（c）所示；若支护结构与围岩之间充填密实，接触良好，此时除设置径向弹性支承外，还可设置切向弹性支承，如图6-3-6（d）所示。对于弹性固定的边墙底部可用一个既能约束水平位移，又能产生转动和垂直位移的弹性支座来模拟。

(www.xing528.com)

图6-3-6　弹性支承设置方式

图6-3-7为隧道支护结构内力分析的计算图式。将主动围岩压力简化为节点荷载，支护结构的内力计算，可采用矩阵力法或矩阵位移法，编制程序进行分析计算。

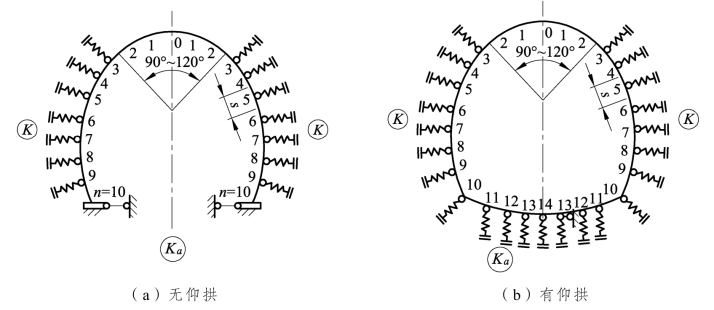
图6-3-7　弹性支承法计算模型

以矩阵位移法为例介绍如下：

（1）矩阵位移法基本原理。

矩阵位移法又叫直接刚度法，它以结构节点位移为基本未知量，其原理是：连接在同一节点各单元的节点位移应该相等，并等于该点的结构节点位移（变形协调条件）；同时作用于某一结构节点的荷载必须与该节点上作用的各个单元的节点力相平衡（静力平衡条件）。首先进行单元分析，找到单元节点力和单元节点位移的关系——单元刚度矩阵，而后进行整体分析，将每一个节点上有共同位移的各单元刚度矩阵元素简单叠加起来，建立以节点静力平衡为条件的结构刚度方程；再利用边界条件，由结构刚度方程中解出未知的结构各节点的位移，也就是解结构刚度方程，然后再根据变形协调条件，求得汇交于该节点各单元的单元节点位移，进而求出单元节点力——衬砌内力。直接刚度法计算过程规范，可以充分发挥电子计算机的自动化效能，有利于编制程序，是目前广为使用的一种方法。其一般计算过程如下：

① 对隧道衬砌整体结构沿其轴线进行离散，计算各分块单元的基本几何参数；选择结构坐标系和局部坐标系，对各节点和单元进行编号；并对用围岩弹性抗力支承链杆进行设置。

② 把所有节点荷载沿结构坐标系分解，建立节点荷载列向量和节点位移向量的关系式。

③ 利用各单元在局部坐标系中的单元刚度矩阵公式，计算局部坐标系中各单元的刚度矩阵。

④ 进行坐标转换，并将单元刚度矩阵按“对号入座”法则叠加到结构刚度矩阵中。

⑤ 引入边界约束条件，修改结构刚度矩阵，计算各节点位移；必要时对弹性支承链杆的设置进行调整。

⑥ 利用杆件在结构坐标系中的单元刚度方程公式，计算结构坐标系中由节点位移产生的节点力。

（2）衬砌结构的处理。

隧道衬砌属于实体的拱形结构，这种结构受弯矩和轴力的影响较大，因此要把衬砌沿其轴线离散化为一些同时能承受弯矩和轴力的直杆单元（梁单元），并将单元的连接点称为节点。同时，假定单元是等厚度的，其计算厚度取为单元两端厚度的平均值。单元的数目视计算精度的需要而定，为了保证衬砌内力分析的精度要求，隧道衬砌一般划分为30个单元以上，但单元数目也不需要太多，一般在60个单元以内。

隧道边墙的底端是直接放在岩层上的，故可以假设边墙底端是弹性固定的，即能产生转动和垂直下沉。但由于边墙底面和围岩之间摩擦力甚大，一般不能产生水平位移，故应在边墙底面的水平方向上加以约束。对于一些特殊形式的衬砌，比如拱和边墙的轴线不连续（带耳墙的明洞）或者墙基需要展宽时，需要添加一个特殊单元——刚性单元。刚性单元能承受部分垂直荷载和水平荷载的作用，其单元本身可看作是刚性的，在理论上讲单元的EA和EI均为无穷大。在实际运算中，通常取刚性单元的刚度为普通单元刚度的30倍。

当结构和荷载都对称时，可只取半跨进行计算，此时在拱顶截面处不允许有水平位移和转角位移。为了反映原结构的受力状态，需要在拱顶截面切开的位置设置两根水平链杆作为边界的约束条件。对于结构对称而荷载不对称的情况，由于拱顶截面切开处不允许有相对垂直位移，因此要在拱顶截面切开处设一根竖向链杆以表示原结构的约束状态。

对于有仰拱的曲墙式衬砌，由于仰拱一般是在拱圈和边墙受力变形基本稳定后才修建的，因此通常可忽略仰拱对衬砌内力的影响。如需要在计算中考虑仰拱的作用，可将仰拱也划分为梁单元，仰拱、边墙、拱圈三者一并考虑进行计算。

（3）等效节点荷载的处理。

在实际工程结构中，主动荷载和结构自重一般不直接作用在节点上。为了配合衬砌的离散化，主动荷载和结构自重也要进行离散，也就是将作用在衬砌上的分布荷载置换成作用在节点上的等效节点荷载。

荷载的转换按简支梁分配的原则进行置换，而不计作用力迁移位置时所引起的力矩的影响。对于竖向或水平的分布荷载，其等效节点力分别近似地取为节点两相邻单元水平或垂直投影长度的一半乘以衬砌计算宽度这一面积范围内的分布荷载的总和。对于衬砌自重，其等效节点力可近似地取为节点两相邻单元重量的一半。由于荷载本身计算的准确性较差，按近似方法计算对最终的结果影响不大，故该方法得到了较为广泛的应用。

（4）弹性支承的调整。

对已进行边界约束处理的结构刚度方程求解，即可得出第一次近似的节点位移值。当计算出某点的水平位移分量ui＜0时，即表明衬砌是向着隧道内变形的，故应将该点的弹性支承链杆i从计算图式中去掉，修改结构总刚度矩阵中的有关元素，重新求解节点位移，直至凡布置有链杆支承处都符合ui≥0的条件为止。

（5）直接刚度法计算流程图。

具体采用直接刚度法进行隧道衬砌结构计算的流程如图6-3-8所示。