模型校正的目的是获取一套增长的参数集(即5个模拟系数的值),从而对研究区的城市增长进行有效模拟。模型校正是SLEUTH模型的核心之一,SLEUTH模型中5个模拟系数的范围都在0~100之间。模型采用强制蒙特卡洛迭代计算法(Brute-force Monte Carlo Method)进行参数的校正,参数校正分为粗校正(Coarse Calibration)、精校正(Fine Calibration)和终校正(Final Calibration)三个阶段进行,每个步骤得到的一套增长的参数集都用于下一个步骤的参数校准,并不断缩小各系数的取值范围,利用实验结果与真实数据进行对比,可以生成一系列统计量,用以评估模拟结果的精度。最后,经过模型自校正过程,并通过预测参数获取(Deriving forecasting coefficients),得到模型的最优参数集,用于模型的多情景预测过程。
1)粗校正
模型校准的初始阶段,首先通过“重采样”工具将所有输入模型图层数据的空间分辨率转换为240m×240m,并将这些输入数据图层放置在c:\cygwin\bin\s\Input\jinan240文件夹中。然后,将模型中5个模拟系数的取值范围均设置为0~100,采用25的步长值,即按照{0,25,50,75,100}进行取值,为了减少模型计算时间,采用3次蒙特卡罗迭代。
粗校正的过程简要说明如下:
▷ 步骤1:修改粗校正文件。
首先,用写字板打开c:\cygwin\bin\s\Scenarios\目录下的scenario.demo200_calibrate文件,另存为scenario.jinan240_calibrate,并依次修改文本中的相关内容(图9-7,修改后的文件详见光盘数据文件\SLEUTH\Scenarios\scenario.jinan240_calibrate)。
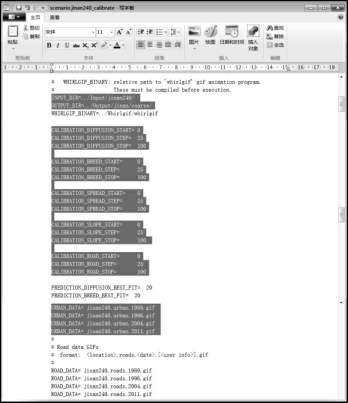
图9-7 粗校正scenario.demo200_calibrate文件中部分语句的修改
▷ 步骤2:在DOS中运行粗校正文件。
首先,在Windows系统下启动DOS命令窗口,并进入c:\cygwin\bin\s\Scenarios目录下(图9-4)。然后,键入命令行“..\grow calibrate scenario.jinan240_calibrate”启动粗校正测试程序(scenario.jinan240_calibrate)来进行SLEUTH模型的粗校正(图9-8、图9-9)。校正通常需要耗费较长的时间,因为模型校正过程使用穷举法(尝试所有可能的参数组合进行模拟,并比较结果的拟合优度)或者遗传算法进行连续搜索,直到得到“最优的”参数集。很多研究文献认为应根据研究区尺度来选取合适的空间分辨率数据,数据精度有时并非越高越好,即过高分辨率的数据不一定会得到比适宜尺度更高的模拟精度。最后,校正完成后,数据文件存放在c:\cygwin\bin\s\Output\目录下建立的coarse文件夹下。
图9-8 粗校正程序在命令提示符窗口中启动
图9-9 粗校正程序在命令提示符窗口中运行
▷ 步骤3:查看粗校正结果文件。(https://www.xing528.com)
首先,用Excel打开coarse文件夹下的control_stats_pe_0.log文件,并另存为jinancoarse.xlsx文件(图9-10)。表中共有记录了3124次运算的3124条模拟结果,其中包含13个表征模拟精度的指数(不进行土地利用变化模拟时为12个有效指数)和5个模拟参数(图9-10)。

图9-10 粗校正得到的13个指数集与5个参数集
然后,最佳参数组合的选取和5个系数取值范围的确定。模型校正阶段会产生一系列的模型准确性判定指数,且在选择哪些指数能够更好表征模型的精度问题上存在较大争论,也有很多不同的选取方法。本例根据研究区实际,参考相关文献,采用Compare、Pop、Edges、Cluster、Slope、Xmean、Ymean等7个指数的乘积即OSM(the Optimal SLEUTH Metric)作为模型校正和参数区间缩小的主要判据。选取乘积排在前5位的模拟结果(如果得分第5存在得分相同的情况,则考虑所有同分模拟结果),从而缩小5个系数的取值范围,产生5个新的系数区段(图9-11)。根据排序结果(取前8位),扩散系数(Diffusion,即表中的Diff字段)为1,在下一步校正中使用1~25的范围,繁殖系数(Breed,即表中的Brd字段)在1~50之间,传播系数(Spread,即表中的Sprd字段)在25~100之间,坡度系数(Slope,即表中的Slp字段)在1~25之间,道路引力系数(Road Gravity,即表中的RG字段)变化幅度很大,但大部分在50~100之间(选取的下一步校正的参数区间和步长参见表9-2)。

图9-11 按照7个指数乘积进行排序的结果
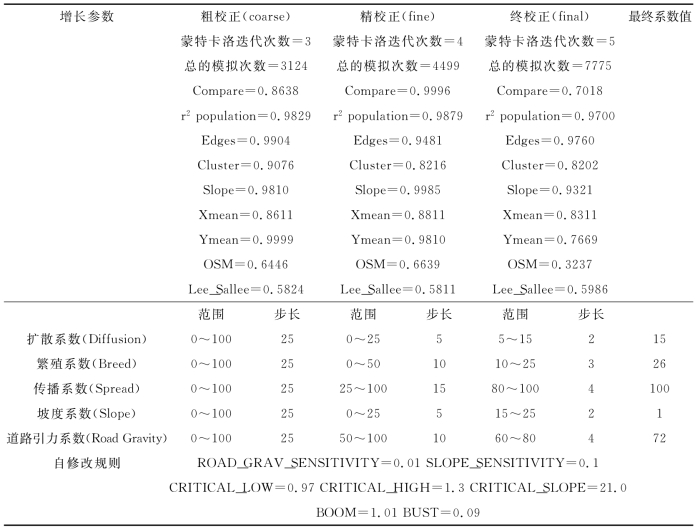
表9-2 SLEUTH模型校正阶段主要指数与参数统计结果
2)精校正
首先,通过“重采样”工具将所有输入模型图层数据的空间分辨率转换为120m×120m,然后修改校正程序的相关文本。在该阶段,采用4次蒙特卡罗迭代。根据选择的增长系数值区间和步长,参照粗校正阶段的过程修改校正文本,得到精校准的程序文本scenario.jinan120_calibrate。然后,在DOS中运行精校正文件,得到校正结果。最后,计算OSM值,并参照其排名前列的模拟结果系数值进一步缩小5个系数的取值范围(表9-2)。
3)终校正
采用同样的校正过程,进行模型的终校正(精校准使用的程序文本为scenario.jinan 60_calibrate)。在该阶段,采用5次蒙特卡罗迭代,所有输入模型图层数据的空间分辨率均为数据初始的分辨率60m×60m。
4)模拟参数获取(Deriving forecasting coefficients)
终校正完成后,还需要进行模拟参数获取(即Derive阶段)。在该阶段,通过同样的方法进一步缩减参数的取值范围。根据终校正的排序结果(排序第一的结果),扩散系数(Diffusion)的为13,繁殖系数(Breed)为22,传播系数(Spread)为96,坡度系数(Slope)为17,道路引力系数(Road Gravity)为60,将这5个系数的取值填进程序文本的参数设置部分中。然后,取步长为1,采用100次蒙特卡罗迭代进行模拟参数的获取。最后,在该阶段生成的avg_pe_0.log文件中,将结束年份(最后一行)的5个增长系数进行四舍五入后,作为模型模拟的最佳预测参数组合。最终生成的5个系数值分别为:扩散系数15、繁殖系数26、传播系数100、坡度系数1和道路引力系数72(表9-2)。由于模拟指数选取以及蒙特卡洛迭代次数的差异,本例中经自修改规则后,最优系数组合变化较大。在具体的研究案例中,应按照研究区实际合理选取模拟指数和蒙特卡洛迭代次数,以便获得最好的校正结果。
由表9-2可见,模型校正得到的最终系数值中,传播系数最大(100),表明其对城市用地增长具有重要影响,研究区城市用地增长主要以城市边缘增长为主;道路引力系数也很高(74),仅次于传播系数,说明道路对研究区城市用地的增长也具有重要影响,TOD发展模式也是研究区城市用地增长的重要模式;繁殖系数不大(仅为26),且扩散系数也较小(仅为15),说明自发增长形成的新城市中心增长的可能性不高,表明研究区新城市中心用地增长模式不明显;另外,坡度系数为1,说明研究区地形条件对城市用地增长的抑制作用非常有限。综上所述,研究区主要受传播系数与道路引力系数的影响,城市用地增长主要为发生在城市边缘和道路可达性较高的区域。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




