基于层次分析法的综合竞争力评价实例

层次分析法（Analytic Hierarchy Process，AHP）是20世纪70年代中期由美国运筹学家T.L.Saaty（托马斯·L.萨迪）提出的一种定性和定量相结合的、系统化、层次化（将与决策有关的元素分解成目标、准则、方案等层次）的分析方法。该方法的特点是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法，尤其适合于对决策结果难于直接准确计量的场合。

由于AHP在处理复杂的决策问题上的实用性和有效性，很快在世界范围得到重视，它的应用已遍及经济计划和管理、能源政策和分配、行为科学、军事指挥、运输、农业、教育、人才、医疗、环境等领域。

AHP采用先分解后综合的系统思想，通过整理和综合人们的主观判断，使定性分析与定量分析有机结合，实现定量化决策。其基本步骤为：建立递阶层次结构——构建两两判别矩阵——进行层次排序与一致性检验。

▷　步骤1：建立递阶层次结构。

通过调查研究和分析弄清楚决策问题的范围和目标，问题包含的因素，各因素之间的相互作用关系；然后将各个因素按照它们的性质聚集成组，并把它们的共同特征看成是系统中高一层次中的一些因素，而这些因素又按照另外一些特性被组合，从而形成更高层次的因素，直到最终形成单一的最高目标（这往往就是决策问题的总目标）。如此，构成了一个以目标层、若干准则层和方案层所组成的递阶层次结构。

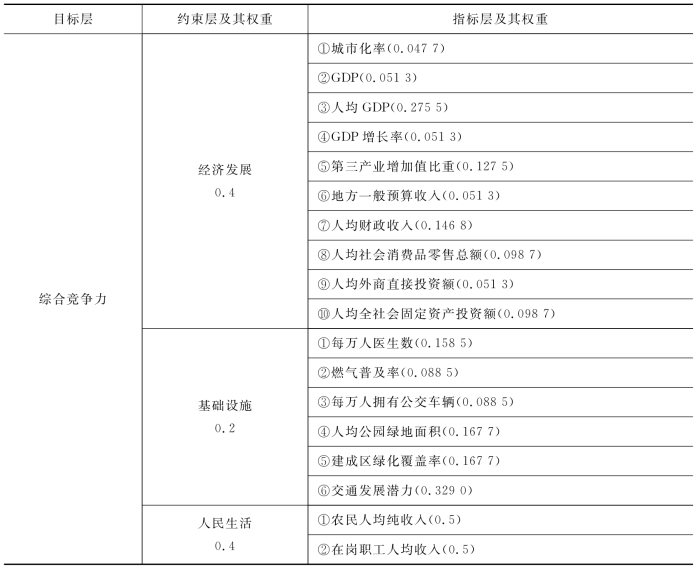
本例中，使用图4-1中的层次结构，即目标层为综合竞争力（综合实力），约束层包括经济发展、基础设施和人民生活三个方面，指标层包括19个具体的指标（图4-1）。

▷　步骤2：构建两两判别矩阵。

如果有一组物体，需要知道它们的重量，而又没有衡器，那么就可以通过两两比较它们的相互重量，得出每对物体重量比的判断，从而构成判断矩阵；然后通过求解判断矩阵的最大特征值和它所对应的特征向量，就可以得出这一组物体的相对重量。

构建两两判别矩阵是定量表征一组变量相对重要性的重要手段。按照表4-4相对重要性权数的定义来构建冀中南指标层和约束层的两两判别矩阵（表4-5～表4-7）。由于人民生活约束层下仅有两个指标，可将两个指标设置为相同权重，即各为0.50。

表4-4　两两判别矩阵中相对重要性权数的定义

注：两两比较时，前者比后者相对不重要些，则采用以上标度的倒数表示。

表4-5　经济发展约束层下各指标的两两判别矩阵

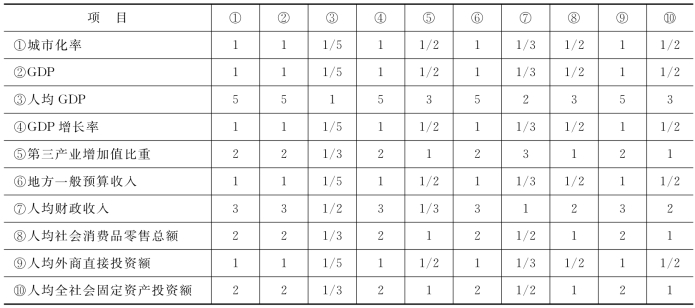
表4-6　基础设施约束层下各指标的两两判别矩阵

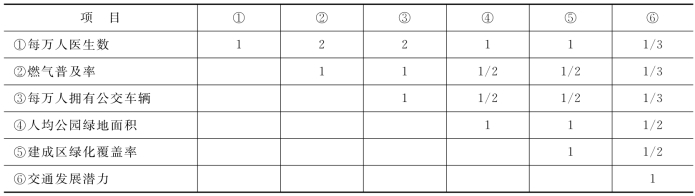
表4-7　约束层的两两判别矩阵

▷　步骤3：进行层次排序与一致性检验。

层次排序的目的是对于上一层次中的某元素而言，确定本层次与之有联系的各元素重要性次序的权重值。它是本层次所有元素对上一层次某元素而言的重要性排序的数据基础。

层次排序的任务可以归结为计算判断矩阵的特征根和特征向量问题，即对于判断矩阵A，计算满足AW＝λmaxW，可以用线性代数知识求解，并且能够用计算机求得高精度的结果。但事实上，在AHP决策分析中，判断矩阵的最大特征根及其所对应的特征向量的计算并不需要太高的精度。用户可以采用方根法与和积法两种近似算法求解。

（1）用方根法计算最大特征根及其所对应的特征向量

首先，计算判别矩阵每一行元素的乘积Mi。

然后，计算Mi的n次方根Ni。

再次，将向量Ni归一化得特征向量Wi（可采用总和标准化方法）。

最后，采用下面的公式计算最大特征根λmax。

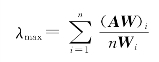
这里以约束层的两两判别矩阵的求解过程为例加以说明。

（2）用和积法计算最大特征根及其所对应的特征向量(www.xing528.com)

首先，将判别矩阵每一列元素进行归一化M（一般可采用总和归一化方法）。

然后，将所得矩阵M按行进行求和得到N。

再次，将向量N再归一化得特征向量Wi。

最后，采用前面的公式计算最大特征根λmax。

下面以约束层下的经济发展指标的两两判别矩阵的求解过程为例加以说明。

用户可以采用同样的方法计算基础设施指标层的最大特征根及其所对应的特征向量。

在计算完最大特征根及其所对应的特征向量后，需要进行一致性检验。

当判断矩阵A具有完全一致性时，λmax＝n。但是，在一般情况下是很难做到完全一致性的。为了检验判断矩阵的一致性，需要计算它的一致性指标CI（Consistency Index）。当CI＝0时，判断矩阵具有完全一致性；CI越大，一致性越差。

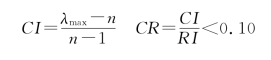
为了检验判断矩阵是否具有令人满意的一致性，需要将CI与平均随机一致性指标RI（Random Index）进行比较。

判断矩阵的随机一致性比例的求算。首先，分别对3～10阶递阶层次结构各构造500个随机样本矩阵。其次，随机用1～9标度填满样本矩阵上三角各项，对角线各要素为1，转置位置项为上述对应位置的随机数的倒数。最后，对500个随机样本矩阵分别计算一致性指标值，然后求取平均值，即得到平均随机一致性指标RI。

一致性指标CI与同阶平均随机一致性指标RI之比，称为随机一致性比例，记为CR（Consistency Ratio）。

一般当CR＜0.10时，就认为判断矩阵具有令人满意的一致性，当CR≥0.10时，就需要调整判断矩阵，直到满意为止。

首先，对每一个约束层下的指标体系进行层次单排序与一致性检验。此处以社会经济约束因子层为例加以说明。

查RI对照表可得，当n＝10时，RI＝1.49。计算得到CR为0.013，远小于0.10，通过一致性检验。

其次，对约束层的3个因子进行一致性检验。CR＝0，远小于0.10，通过一致性检验。

最后，得到了每一个约束层和每一个指标的权重值（表4-8）。

表4-8　冀中南区域综合竞争力评价指标体系与权重

▷　步骤4：综合实力评价与等级划分。

由于原始指标体系中的指标值量纲不一致，数值差异显著，因而首先采用极差标准化方法将指标原始值进行归一化处理（无量纲化处理），这一步骤可以在EXCEL中完成。极差标准化时需要特别注意反向指标的处理。

然后，根据前面计算的权重，进行加权求和计算得到每一个县市的综合得分值。为了便于区分，将综合得分值进行极差标准化，并将其归一化值乘以100得到最后的总得分（表4-9）。

表4-9　基于层次分析法的综合竞争力标准化得分值

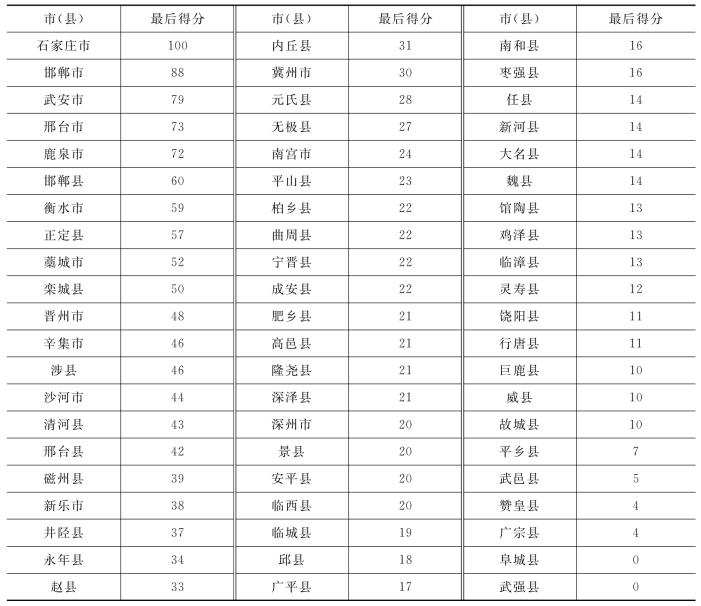
根据总得分值，将规划研究区划分为3类。总得分大于55的划分为第一类，主要包括石家庄市、邯郸市、武安市、邢台市、鹿泉市、邯郸县、衡水市、正定县等8个县市；总得分大于或等于30且小于或等于55的划分为第二类，主要包括藁城市、栾城县、晋州市、辛集市、涉县、沙河市等15个县市；总得分小于30的划分为第三类，主要包括武邑县、赞皇县、广宗县、阜城县、武强县等40个县市。

与前面的分析结果进行对比，可以发现，聚类分析根据N维空间的距离大小进行类别的划分，但类别的概念相对较为模糊，即类别不一定就是代表综合竞争力的强弱。主成分分析和层次分析法的综合得分值很好的代表了竞争力的大小，能够得到较为科学的分类结果，但采用的方法不一样，通常得到的结果会存在一定的差异。因此，在城市与区域规划与研究过程中要具体问题具体分析。