基于主成分分析的综合竞争力评价方法

在分析处理多变量问题时，变量间往往存在一定的相关性，有些变量之间密切相关，使观测数据所反映的信息多有重叠，因此，人们希望能够找出较少的彼此之间互不相关的综合变量尽可能反映原来变量的信息，以达到数据简化（Data Reduction）的目的。显然，在一个低维空间解释系统要比在高维系统容易得多。

因子分析（Factor Analysis，FA）就是用少数几个因子来描述许多指标或因素之间的联系，以较少的几个因子来反映原始资料的大部分信息的统计学分析方法。例如，美国统计学家Stone在1947年关于国民经济的研究中，根据美国1927—1938年的数据，得到17个反映国民收入与支出的变量因素，经过因子分析，得到3个新变量，可以解释17个原始变量97.4%的信息；英国统计学家Moser Scott在1961年对英国157个城镇发展水平进行调查时，原始测量的变量有57个，而通过因子分析发现，只需用5个新的综合变量就可以解释95%的原始信息。

从数学角度来看，因子分析是一种化繁为简的降维处理技术，其应用非常广泛，非常适用于城市与区域综合竞争力的评价。

主成分分析（Principal Component Analysis，PCA）是因子分析的一个特例和一种类型，是使用最多的因子提取方法。它通过坐标变换手段，将原有的多个相关变量，做线性变化，转换为另外一组不相关的变量。选取前面几个方差最大的主成分，这样达到了因子分析较少变量个数的目的，同时又能用较少的变量反映原有变量的绝大部分的信息。

主成分分析具有以下4个主要特点：

①因子变量的数量远少于原有的指标变量的数量，因而对因子变量的分析能够减少分析中的工作量。②因子变量不是对原始变量的取舍，而是根据原始变量的信息进行重新组构，它能够反映原有变量大部分的信息。③因子变量之间不存在显著的线性相关关系，对变量的分析比较方便，但原始部分变量之间多存在较显著的相关关系。④因子变量具有命名解释性，即该变量是对某些原始变量信息的综合和反映。

根据研究对象的不同，把因子分析分为R型和Q型两种。当研究对象是变量时，属于R型因子分析；当研究对象是样品时，属于Q型因子分析。但有的因子分析方法兼有R型和Q型因子分析的一些特点，如因子分析中的对应分析方法，有的学者称之为双重型因子分析，以示与其他两类的区别。

这里以冀中南数据为例介绍PASW Statistics 18中主成分分析的具体应用。

▷　步骤1：在PASW Statistics 18中打开“冀中南分类分析.sav”数据文件。

▷　步骤2：使用“因子分析”工具进行R型因子分析。

首先，点击工具条上的“分析”—“降维”—“因子分析”，弹出“因子分析”对话框（图4-23）。将对话框左侧变量列表中的除“市（县）”变量外的其他所有变量加载到“变量”栏中。

图4-23　“因子分析”对话框

图4-24　“因子分析：描述统计”对话框

然后，点击“因子分析”对话框中的“描述”按钮，弹出“描述统计”对话框（图4-24）。“统计量”栏中有两个选项：“单变量描述性”（输出变量均值、标准差等）和“原始分析结果”（默认设置，输出初始公因子方差、特征值及其变量解释的百分比等）。本例中两项都选。“相关矩阵”栏中有7个选项，提供了7种检验变量是否适合做因子分析的检验方法，分别是系数（相关系数矩阵）、显著性水平、行列式（相关系数矩阵的行列式）、逆模型（相关系数矩阵的逆矩阵）、再生（再生相关矩阵，原始相关与再生相关的差值）、反映象（反映象相关矩阵检验）、KMO和Bartlett的球形度检验。

下面就常用的几个因子分析检验方法做简要解释。

（1）Bartlett的球形度检验。该检验以变量的相关系数矩阵作为出发点，它的零假设H0为相关系数矩阵是一个单位阵，即相关系数矩阵对角线上的所有元素都为1，而所有非对角线上的元素都为0，即原始变量两两之间不相关。Bartlett球形检验的统计量是根据相关系数矩阵的行列式得到。如果该值较大，且其对应的相伴概率值小于用户指定的显著性水平，那么就应拒绝零假设H0，认为相关系数不可能是单位阵，也即原始变量间存在相关性。

（2）反映象相关矩阵检验。该检验以变量的偏相关系数矩阵作为出发点，将偏相关系数矩阵的每个元素取反，得到反映象相关矩阵。偏相关系数是在控制了其他变量影响的条件下计算出来的相关系数，如果变量之间存在越多的重叠影响，那么偏相关系数就会越小，这些变量越适合进行因子分析。

（3）KMO（Kaiser-Meyer-Olkin）检验。该检验的统计量用于比较变量之间的简单相关和偏相关系数。KMO值介于0～1，越接近1，表明所有变量之间简单相关系数平方和远大于偏相关系数平方和，越适合因子分析。其中，Kaiser给出一个KMO检验标准：KMO＞0.9，非常适合；0.8＜KMO＜0.9，适合；0.7＜KMO＜0.8，一般；0.6＜KMO＜0.7，不太适合；KMO＜0.5，不适合。

本例中，选择常用的系数、显著性水平、反映象、KMO和Bartlett的球形度检验4个选项。单击“继续”按钮，返回“因子分析”对话框。

其次，点击“因子分析”对话框中的“抽取”按钮，弹出“抽取”对话框（图4-25）。在“方法”栏中提供了因子分析的7种方法，本例采用默认的主成分方法。

图4-25　“因子分析：抽取”对话框

主成分（Principle Components Analysis），为默认的提取方法，该方法形成观察变量间不相关的线性组合，第一个成分具有最大的方差，其余的成分对方差解释的比例逐渐变小，且各成分间均不相关。

未加权的最小平方法（Unweighted least squares），该方法使观察的相关性矩阵和再生相关矩阵之差的平方和最小。

综合最小平方法（Generalized least squares），又称广义最小二乘法，该方法可以使观察值的相关性矩阵和再生相关性矩阵之间的差的平方和最小。

最大似然（Maximum likelihood），在样本来自多变量正态分布的情况下，它生成的参数估计最有可能生成观察到的相关矩阵。

主轴因子分解（Principal axis factoring），从原始相关矩阵提取公因子，将多元相关系数的平方代替对角线的值作为公因子方差的初始估计值，应估计新公因子方差的因子载荷替代对角线中旧的公因子方差。当公因子方差的改变符合收敛准则的要求时，将终止迭代过程。

α因子分解（Alpha factoring），把分析的变量看做来自一个潜在总体的样本，使因子的α可靠性系数最大。

映象因子分解（Image factoring），把部分映象（变量的公共部分）看做剩余变量的线性回归。

“分析”栏中有相关性矩阵（默认设置）和协方差矩阵两项。本例采用默认设置。

“输出”栏中有未旋转的因子解（默认设置，显示未旋转的因子载荷、公因子方差及因子解的特征值）和碎石图（以降序方式显示与成分或因子关联的特征值以及成分或因子的数量）两项。本例两项均选择。

“抽取”栏用于定义因子个数的提取标准，有两种方式：基于特征值（默认设置，特征值大于1）和因子的固定数量（用户可以定义要提取的因子数量）。本例采用默认设置。

“最大收敛性迭代次数”用于定义因子分析收敛的最大迭代次数，系统默认的最大迭代次数为25。本例采用默认设置。点击“继续”按钮，返回“因子分析”对话框。

图4-26　“因子分析：旋转”对话框

再次，点击“因子分析”对话框中的“旋转”按钮，弹出“旋转”对话框（图4-26），选择因子旋转方法。系统共提供了最大方差法（又称方差最大正交旋转法，使每个因子中具有最高载荷的变量数最小的正交旋转法，可简化因子的解释）、直接Oblimin方法（又称直接斜交旋转法，当Delta值为0时，结果为最大斜交，Delta值越小，因子的斜交程度越小，Delta值的范围是（-1，0））、最大四次方值法（使需要解释的每个变量的因子数最小，可简化对观察变量的解释）、最大平衡值法（又称相等最大正交旋转法，是方差最大正交旋转法与最大四次方值法的组合，使每个因子中具有最高载荷的变量数量最小及需要解释的每个变量的因子数最小）、Promax（最优斜交旋转，进行因子的校正，适用于大样本数据，并同时给出Kappa值，默认值为4）。因子旋转目的是为了简化结构，以帮助我们解释因子。系统默认不进行旋转（无），本例选择最大方差法。

“输出”栏中有两个选项，“旋转解”（输出旋转后的因子载荷矩阵）和“载荷图”（输出载荷散点图）。本例两项均选择。

本例“最大收敛性迭代次数”采用默认设置。点击“继续”按钮，返回“因子分析”对话框。

图4-27　“因子分析：因子得分”对话框

然后，点击“因子分析”对话框中的“得分”按钮，弹出“因子得分”对话框（图4-27），对因子得分进行设置。点击选择“保存为变量”（将最终的因子得分保存到新变量中），系统提供了因子得分的3种计算方法。本例选择“回归”方法。

回归（Regression）：因子得分均值为0，采用多元相关平方。

Bartlett（巴特利法）：因子得分均值为0，采用超出变量范围各因子平方和被最小化。(www.xing528.com)

Anderson-Rubin（安德森-洛宾法）：因子得分均值为0，标准差1，彼此不相关。

点击选择“显示因子得分系数矩阵”，点击“继续”按钮，返回“因子分析”对话框。

图4-28　“因子分析：选项”对话框

最后，点击“因子分析”对话框中的“选项”按钮，弹出“选项”对话框（图4-28）。在“缺失值”栏中定义缺失值的处理方式，系统提供三种方法：按列表排除个案（Exclude cases listwise，默认设置，去除所有缺失值的个案）、按对排除个案（Exclude cases pairwise，含有缺失值的变量，去掉该案例）、使用均值替换（Replace with mean，用平均值代替缺失值）。

成对删除（pairwise）的意思是如果一个个案（case）中有若干个变量数据，其中某一个或者多个变量数据缺失，那么这个个案（case）中所有的数据就会被删掉不纳入计算；另外一个成列（listwise）删除，就是说如果用到了某个个案中缺失的数据就会自动将此个案删除，但是在对其他无缺失数据的变量进行计算时，此个案还被纳入计算。本例选择默认设置按列表排除个案。

“系数显示格式”用于控制因子得分系统矩阵的显示格式，一种是按大小排序，一种是取消小系数（排除绝对值小于用户定义值的系数）。本例选择按大小排序。点击“继续”按钮，返回“因子分析”对话框。点击“确定”按钮，执行因子分析命令，得到因子分析结果，并将文件保存在shiyan04文件夹下，命名为“主成分分析结果.spv”。

▷　步骤3：因子分析结果的简要解释。

按照输出结果表格的顺序分别进行简要的解释说明。

（1）描述统计量表，存储了变量的均值、标准差和分析的个案数等基本统计信息。

（2）相关矩阵表（图4-29）。通过相关矩阵可以看出哪些变量之间存在高相关。存在高相关也说明原始变量之间存在高信息重叠。

图4-29　因子分析结果中的相关矩阵

（3）KMO和Bartlett的检验结果表（图4-30）。该结果是是否适合进行因子分析的重要参照，因此，因子分析需要首先按照此分析结果进行判定。本例中，KMO检验值为0.823，大于0.6，适合因子分析；Bartlett的检验相伴概率为0.000，小于显著性水平0.01，同样适合因子分析。因此，该例适合进行因子分析。

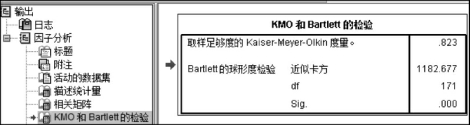
图4-30　因子分析结果中的KMO和Bartlett的检验

（4）反映象矩阵表。

（5）公因子方差表（图4-31），给出了初始变量的共同度。这是因子分析的初始结果，该表格的第1列列出了所有原始变量的名称；第2列为初始变量共同度；第3列是根据因子分析最终解计算出的变量共同度。根据最终提取的m个特征值和对应的特征向量计算出因子载荷矩阵。这时由于因子变量个数少于原始变量的个数，因此每个变量的共同度必然小于1。例如，总人口的共同度为0.885，可以理解为几个公因子能够解释总人口方差的88.5%。

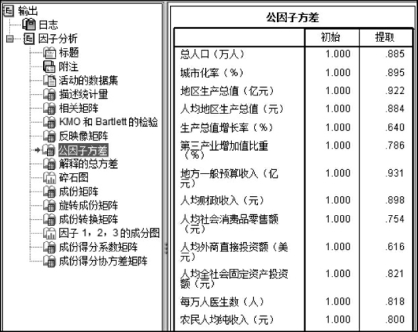
图4-31　因子分析结果中的公因子方差

（6）解释的总方差表（图4-32），又称因子方差贡献率表。该表格是因子分析后因子提取和因子旋转的结果。第1列是因子分析19个初始解序号。第2列是因子变量的方差贡献（特征值），它是衡量因子重要程度的指标。第3列是各因子变量的方差贡献率（%of Variance），表示该因子描述的方差占原有变量总方差的比例。第4列是因子变量的累计方差贡献率，表示前m个因子描述的总方差占原有变量总方差的比例。第5列到第7列则是从初始解中按照一定标准（在前面的分析中设定了提取因子的标准是特征值大于1）提取了4个公共因子后对原变量总体的描述情况。各列数据的含义和前面第2列到第4列相同，可见提取了4个因子后，它们反映了原变量的大部分信息（72.619%）。第8列到第10列是旋转以后得到的因子对原变量总体的刻画情况。一般来说，累积方差贡献率达到70%以上即认为比较满意。

图4-32　因子分析结果中的解释的总方差

提取方法：主成分分析。

（7）碎石图（图4-33）。特征值的大小代表了主成分的方差贡献率的大小和重要性程度。

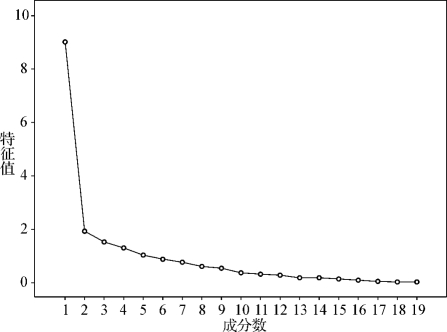
图4-33　因子分析结果中的碎石图

（8）成分矩阵图（图4-34），记录了每一个变量在4个主成分上的载荷矩阵。如果在第1主成分的载荷远大于其他主成分，那么该变量对第1主成分贡献率大，接近第1主成分。根据此特征，可以进行因子的命名和解释。

图4-34　因子分析结果中的成分矩阵

（9）旋转成分矩阵表，记录了经过旋转后的每一个变量在4个主成分上的载荷矩阵。旋转之后的因子载荷矩阵更易解释原始指标是接近哪个主成分变量，更易于因子命名和解释。

（10）成分转换矩阵表。

（11）成分1，2，3的成分图（图4-35），即载荷散点图，是旋转后因子载荷矩阵的图形化表示方式。

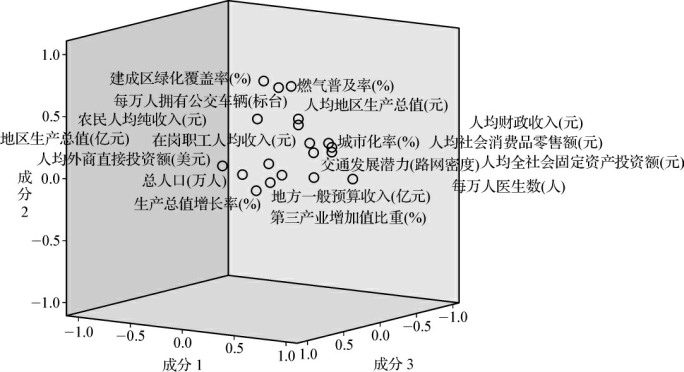
图4-35　因子分析结果中的成分图

（12）成分得分系数矩阵（图4-36）。根据成分得分可以得出最终的因子得分方程。

（13）成分得分协方差矩阵。从协方差矩阵看，不同因子之间的数据为0，因而也证实了因子之间是不相关的。

因子分析最后生成的4个主成分的得分值将作为新列写入原来表格后面。用户可以对4个主成分的方差贡献率进行总和标准化处理，使其总贡献率和为1，计算得到新值作为每个主成分的权重，从而采用加权求和方法计算每个县市的综合得分值。具体步骤为：首先，将“冀中南分类分析.sav”文件另存为EXCEL格式“冀中南分类分析.xls”。然后，将4个主成分的方差贡献率进行总和标准化处理，得到4个主成分的权重，并加权求和得到每一市县的综合得分值。最后，采用极差标准化方法，将综合得分值进行标准化处理，使得分值位于［0，1］区间，为了便于分析，可将综合得分值的标准化得分乘以100，得到各县市的最后综合得分值。

图4-36　因子分析结果中的成分得分系数矩阵

提取方法：主成分。
旋转法：具有Kaiser标准化的正交旋转法。
构成得分。

▷　步骤4：冀中南区域综合竞争力分类。

主成分计算结果虽然没有直接给出综合竞争力的类别，但能够得到一个综合的评价得分值。用户可以根据该得分值，对冀中南区域各县市进行综合判断和分析，进而进行区域综合竞争力类型的划分。

为了和前面的聚类分类结果进行对比，将研究区分为3类，石家庄（100）、邯郸市（76.41）、衡水市（67.11）、邢台市（64.21）为综合竞争力最强的一类，综合竞争力指数值都大于60，明显高于第二类。由此可见，冀中南经济空间格局仍呈现高首位度、高积聚度的总体发展态势，在未来的发展过程中，集聚发展、壮大核心城市仍然是区域发展的核心主题。将综合得分值大于10的县市划分为第二类，包括武安市（33.53）、涉县（26.35）、邯郸县（25.79）、内丘县（21.13）、鹿泉市（21.08）等25个县市。其他综合竞争力得分值低于10的县市划为第三类，包括冀州市（9.86）、无极县（3.52）、临漳县（2.36）、阜城县（1.78）、任县（0.00）等34个县市。

对比聚类分析的结果，可以发现聚类分析是根据样本的亲疏来划分类别的，而主成分分析是通过因子载荷矩阵和特征根等来表征，从而得到因子得分和总得分。两种分析方法得到的结果存在较大的差异。