车辆系统仿真实践：动力传动系统模型

1.模型库结构

履带车辆推进系统的模块化仿真模型主要包括发动机模型、传动系统模型及车辆行动部分模型。其模型结构如图10.3.7所示，发动机模型有一个弹性功率通口，与传动系统连接输出功率；一个输入信号通口，用于输入油门信号；一个输出信号通口，输出转速；传动系统有3个惯性功率通口，分别与发动机和行动系统相连接。

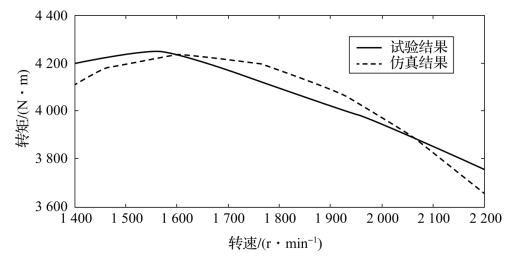
图10.3.6　柴油机外特性仿真与实验值比较

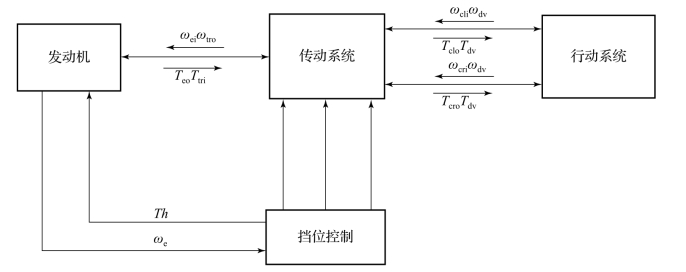
图10.3.7　履带车辆推进系统模块化仿真模型结构

该履带车辆为双侧变速箱结构型式的液力机械传动系统，如图10.3.8所示，主要包括可闭锁式液力变矩器、传动箱、三自由度行星变速箱、液压控制系统、侧传动等5个子系统。

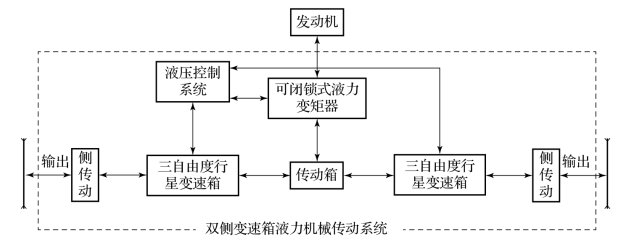
图10.3.8　传动系统模型结构图

根据模块化建模的方法，图10.3.8所示即为动力传动系统的一级子系统，每个子系统又由若干个下一级子系统或基本元件组成。为了使用方便，将模型库的结构分为两种：元件库和系统库。元件库分层结构按照所属工程领域建立，即机械元件库、液压元件库、发动机元件库等。基于元件库，可按从下到上的方法建立各种不同类型车辆动力传动系统模型。系统库按典型履带车辆动力传动系统实际组成建立。系统库适用于相同结构形式动力传动系统的快速建模，可进行子系统更换、参数的修改等操作，提高建模的效率，也可方便地增加子系统模型。履带车辆典型动力传动系统模型库如图10.3.9和10.3.10所示。

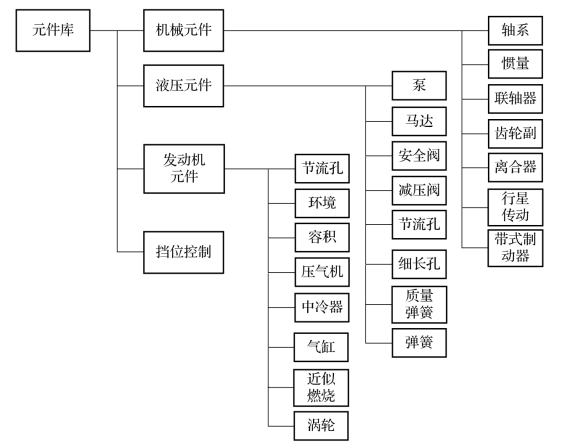
图10.3.9　动力传动系统元件库结构

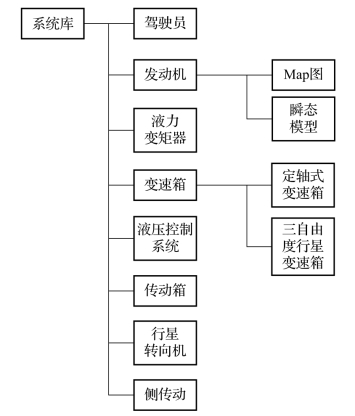
图10.3.10　动力传动系统库结构

2.元部件数学模型

1）基本机械元件

动力传动系统中各部件模型主要由基本的机械元件构成，主要包括轴、惯量、联轴器、齿轮副、行星齿轮机构、离合器等。

（1）无惯量轴（SH）与惯量轴（RS）。

无惯量轴的转动惯量被等效到与其相连接的元件上，不考虑其非线性，这样无惯量轴就被简化为一个弹簧阻尼单元。该模型有两个弹性通口，如图10.3.11（a）、（b）所示。轴的转矩根据轴两端角位移与角速度差计算所得，其动力学方程描述为

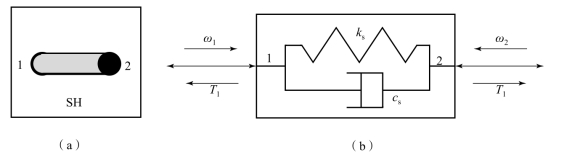
图10.3.11　无惯量轴的动力学模型

（a）模型图标；（b）模型描述

式中　Δθ——轴两端角位移差（rad）；

Δω——轴两端角速度差（rad／s）；

ω1，ω2——分别为轴两通口处角速度（rad／s）；

T1，T2——分别为轴两通口处转矩（N·m）；

ks——轴的扭转刚度（N·m／rad）；

cs——轴的阻尼（N·m·s／rad）。

惯量轴代表一个具有转动惯量的旋转元件，该元件有8个弹性通口，2个惯性通口。图10.3.12为模型图标，其动力学方程描述为

式中　Tt——作用于轴上的总转矩（N·m）；

JS——刚性轴转动惯量（kg·m2）。

（2）惯量（IN）。

惯量模型共有两个惯性通口，如图10.3.13所示，惯量单元动力学方程为

式中　Jin——转动惯量（kg·m2）；

ωin——惯量角速度（rad／s）；

T1，T2——分别为惯量单元两通口处的转矩（N·m）。

（3）联轴器（SD）。

联轴器模型可用具有旋转刚度与阻尼的虚拟轴单元描述，该模型共有两个惯性通口，如图10.3.14所示，其动力学方程为

图10.3.12　惯量轴的模型图标

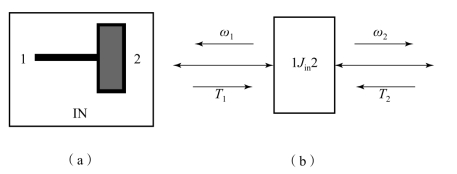
图10.3.13　惯量的动力学模型

（a）模型图标；（b）模型描述

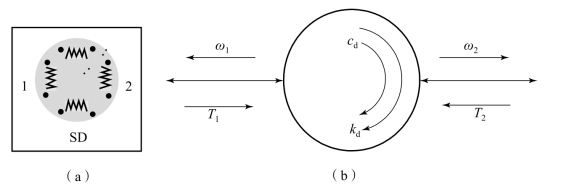
图10.3.14　联轴器的动力学模型

（a）模型图标；（b）模型描述

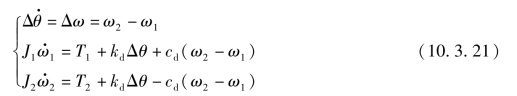
式中　J1，J2——两通口处等效转动惯量（kg·m2）；T1，T2——两通口处转矩（N·m）；

ω1，ω1——两通口处角速度（rad／s）；

kd——扭转刚度（N·m／rad）；

cd——扭转阻尼（N·m·s／rad）；

Δθ——相对扭转角（rad）。

（4）直齿轮副（SG）。

直齿轮传动的动力学模型可被简化为两个惯量系统，齿轮的啮合过程可描述为比例环节及具有旋转刚度与阻尼的虚拟轴单元。直齿轮副共有8个惯性通口，8个通口均可与轴相连接，如图10.3.15所示，其数学模型描述为

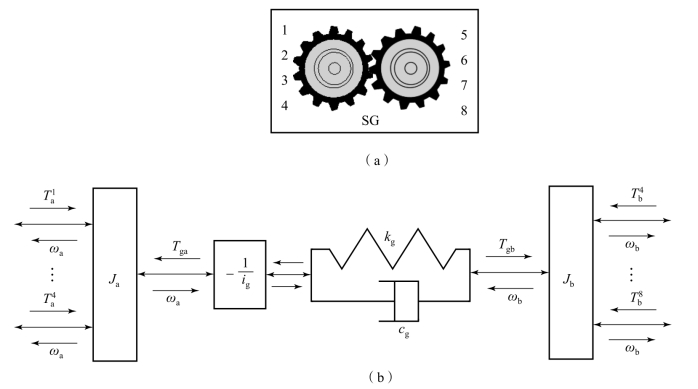
图10.3.15　齿轮副的动力学模型

（a）模型图标；（b）模型描述

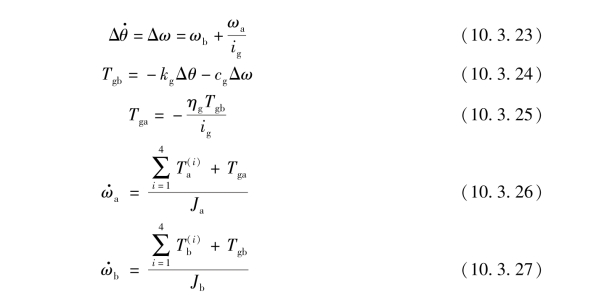
式中　ig——传动比；

za，zb——主、从动齿轮齿数；

Δθ，Δω——虚拟轴角位移差（rad）及角速度差（rad／s）；

ωa，ωb——主、从动齿轮角速度（rad／s）；

kg，cg——齿轮啮合刚度（N·m／rad），啮合阻尼（N·m·s／rad）；

Tga，Tgb——主、从动齿轮啮合转矩（N·m）；

——主、从动齿轮输入转矩（N·m），上标i表示通口数；

Ja，Jb——主、从动齿轮转动惯量（kg·m2）。

（5）斜齿轮副（HG）。

斜齿轮传动动力学模型可被简化为两个惯量系统，斜齿轮的啮合过程可描述为比例环节及具有线性刚度阻尼系统的弹簧阻尼单元。斜齿轮副共有4个惯性通口，4个通口均可与轴相连接，如图10.3.16所示，其数学模型描述为

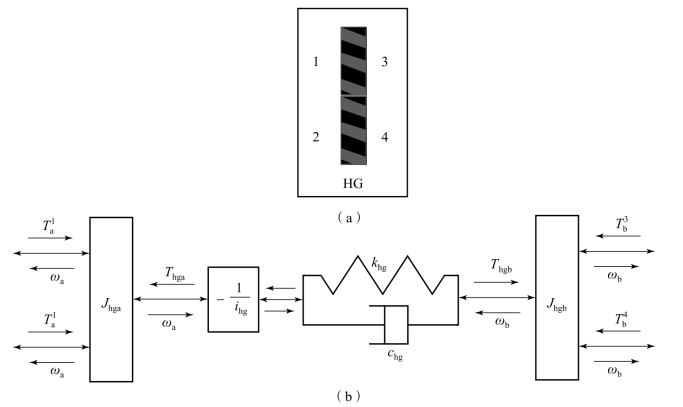
图10.3.16　斜齿轮副的动力学模型

（a）模型图标；（b）模型描述

式中　ihg——传动比；

ra，rb——主、从动斜齿轮节圆半径（m）；

Δl，Δv——弹簧阻尼单元位移差（m）及速度差（m／s）；

ωa，ωb——主、从动斜齿轮角速度（rad／s）；

Fct，FT——斜齿轮传动接触力及其切向分力（N）；

kbg，cbg——齿轮的线性刚度（N／m）、线性阻尼（N·s／m）；

γ，φ——斜齿轮压力角和螺旋角（rad）；

Thga，Thgb——主、从动斜齿轮啮合转矩（N·m）；

——主、从动斜齿轮输入转矩（N·m），上标i表示通口数；

Jhga，Jhgb——主、从动斜齿轮转动惯量（kg·m2）。

（6）锥齿轮副（BG）。

与斜齿轮传动同理，锥齿轮传动动力学模型可被简化为两个惯量系统，锥齿轮的啮合过程可描述为比例环节及具有线性刚度阻尼系统的弹簧阻尼单元。锥齿轮副共有4个通口，4个通口均可与轴相连接，如图10.3.17所示，其数学模型可参照斜齿轮副来描述。

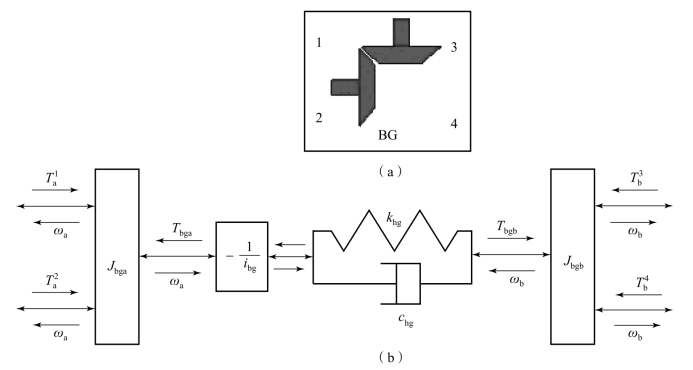
图10.3.17　锥齿轮副的动力学模型

（a）模型图标；（b）模型描述

（7）行星传动（PG）。

行星传动是现代机械传动装置中性能最佳、经济性较好、应用范围最广的一种传动机构。它的种类繁多、形式多样，如行星齿轮传动、摆线针轮行星传动，以及谐波齿轮传动等，都属于行星传动机构。行星传动具有结构紧凑、传动效率高、便于综合分解动力等特点。普通的单行星排由太阳轮s、齿圈q、行星架c、行星轮p等组成，齿轮被简化为两个惯量单元，齿轮之间的啮合过程可描述为具有线性刚度阻尼系统的弹簧阻尼单元，其动力学模型如图10.3.18所示。该模型有s、r、c 3个惯性通口，可以与弹性通口连接。模型中0表示该节点的力相等，输入输出该节点速度为0。

对于太阳轮，其动态方程为

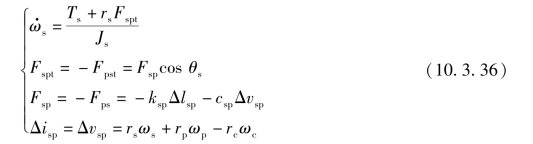
对于齿圈，其动态方程为

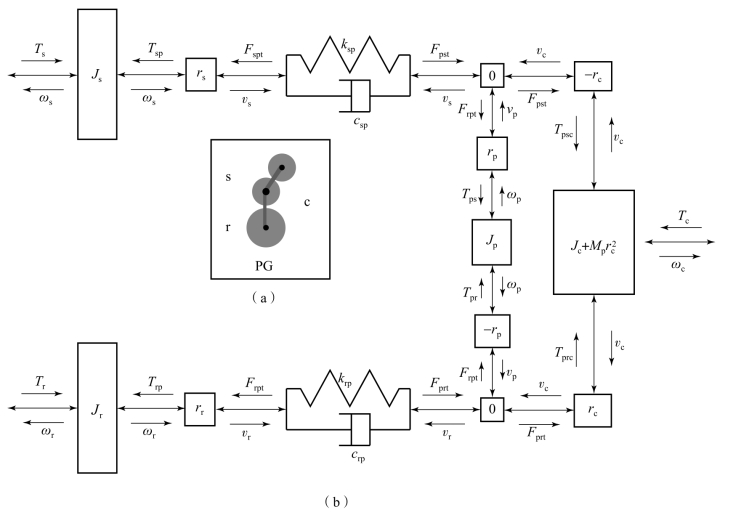
图10.3.18　行星传动的动力学模型

（a）模型图标；（b）模型描述

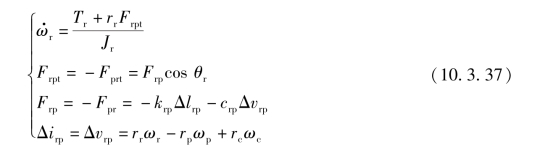
对于行星架及行星轮，其动态方程为

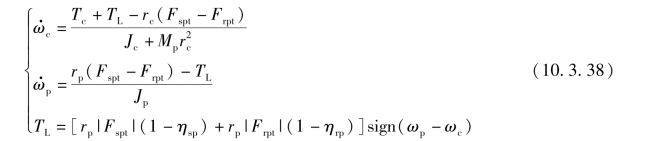
式中　ωs，ωr，ωc，ωp——太阳轮，齿圈，行星架，行星轮角速度（rad／s）；

rs，rr，rc，rp——太阳轮，齿圈，行星架，行星轮节圆半径（m）；

Js，Jr，Jc，Jp——太阳轮，齿圈，行星架，行星轮转动惯量（kg·m2）；

θs，θr——太阳轮与齿圈轮齿压力角（rad）；

Fsp——太阳轮与行星轮的接触力（N）；

Frp——齿圈与行星轮的接触力（N）；

Fspt，Fpst——太阳轮与行星轮接触力的切向分量（N）；

Fspt，Fprt——齿圈与行星轮接触力的切向分量（N）；

Δlsp，Δvsp——太阳轮与行星轮弹簧阻尼单元位移差（m）及速度差（m／s）；

Δlrp，Δvrp——齿圈与行星轮弹簧阻尼单元位移差（m）及速度差（m／s）；

ksp，csp——太阳轮与行星轮啮合线性刚度（N／m），线性阻尼（N·s／m）；

krp，crp——齿圈与行星轮啮合线性刚度（N／m），线性阻尼（N·s／m）；

Mp——行星轮质量（kg）；

ηsp，ηrp——太阳轮与行星轮，齿圈与行星轮啮合效率；

Ts，Tr，Tc，TL——太阳轮，齿圈，行星架输入转矩及行星齿轮传动的损失转矩（N·m）。

（8）湿式离合器、制动器（CP）。

变速箱换挡执行元件包括离合器和制动器两种，二者的工作原理相同，即都是通过摩擦片传递力矩或产生足够的制动力矩，达到换挡要求。如图10.3.19所示，离合器模型有1、2两个惯性通口，与轴相连接；一个容性通口3，与液压控制阀等阻性元件连接。制动器模型与离合器模型基本相同，只是与其连接的轴的另一端输入角速度为零。

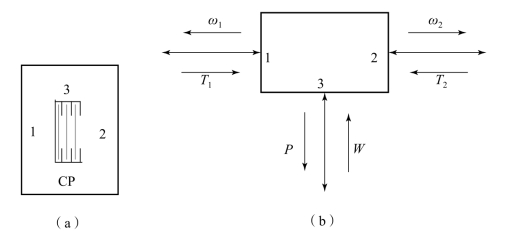
图10.3.19　湿式离合器的动力学模型

（a）模型图标；（b）模型描述

离合器活塞有3种运动状态，用STZS表示：

①STZS＝－1，xc＝0，活塞受回位弹簧预张力的作用，位于初始位置，离合器处于分离状态；

②STZS＝0，0＜xc＜xcmax，活塞在其运动区间内运动，离合器处于分离状态；

③STZS＝1，xc＝xcmax，活塞运动到终止位置，离合器开始摩滑，当主被动边转速相当时，离合器完全结合。

离合器活塞3种运动状态及转换条件如图10.3.20所示。图中，∑F＝pcL Ac＋Fcent－Fseal sign（）。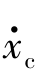

图10.3.20　离合器活塞运动状态及转换条件

在各状态下，离合器活塞的动力学方程为

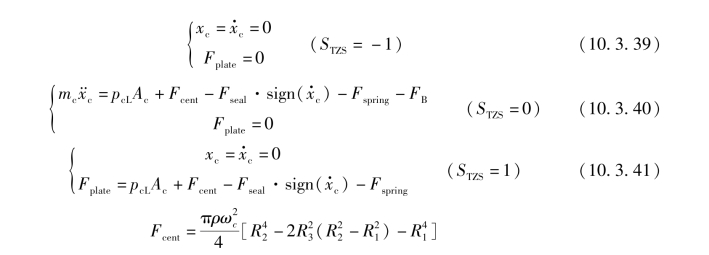
式中　——活塞运动的加速度（m／s2），速度（m／s），位移（m）；

xcmax——活塞最大行程（m）；

mc——活塞及其随动部分的质量（kg）；

Fplate——活塞对离合器的作用力（N）；

pcL——液压油作用到活塞上的压力（Pa）；

Ac——活塞面积（m2）；

r1，r2——活塞内、外半径（m）；

Fcent——离心油压作用到活塞上产生的离心力（N）；

Fseal——活塞密封圈摩擦力（N）；

Fspring——回位弹簧力（N）；

FB——油液对活塞的粘性阻力（N）；

Fconstant——活塞密封圈摩擦力常数量（N）；

R1、R2——活塞内、外半径（m）；

R3——油液进入油缸入口处半径（m）；

ρ——油液密度（kg／m3）；

As——密封圈面积（m2）；

Kc——回位弹簧刚度；

xco——回位弹簧在分离状态下的初始压缩量（m）；

Bc——活塞与缸体的黏性阻尼系数（N·s／m）；

ωc——油缸旋转角速度（rad／s）；

μseal——密封圈摩擦系数。

由于油液的压缩，离合器油缸内压力的变化率为

式中　Ach——离合器油缸的横截面积（m2）；

Win——进入离合器油缸的质量流量（kg／s）；

V0——活塞在初始位置时的离合器油缸初始体积，包括离合器供油管路的体积（m3）；

Vp——离合器油缸体积（m3）；

K——油液体积弹性模量；

ρ——油液平均密度（kg／m3）。

2）液压元件

液压元件可分为容性元件（Storage）、阻性元件（Resistive）、容／阻性元件（Storage／Resistive）3种。容性元件输入输出通口均为容性，输入质量流量W、输出压力p，用S表示；阻性元件输入输出通口均为阻性，输入压力p、输出质量流量W，用R表示；容／阻性元件输入通口为容性，输出通口为阻性，用S／R表示。

各元件之间的连接规范如下：

S→R

R→S

S／R→S／R

S／R→S

R→S／R

根据流体能量守恒原理，对于一容腔，有

式中　ρ——容腔液压油平均密度（kg／m3）；

V——容腔体积（m3）；(www.xing528.com)

Win，Wout——容腔输入输出质量流量（kg／s）。

流体的密度为ρ＝ρ（P，T），其变化率为

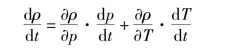
容腔内压力的变化率可描述为

忽略容腔内温度的变化，假设液压油密度为一常数，即为常数，则

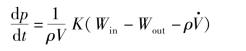
式中　p，T——容腔内压力（Pa），温度（K）；

K——体积弹性模量。

（1）变排量液压元件（PD）。

变排量液压单元工作容腔模型能量转换相当复杂，对其进行数学模型的描述比较困难。本文所建立的变排量液压单元模型中的容积效率、总效率采用试验数据输入，根据系统压力、排量插值获取参数。如图10.3.21所示，该模型有一个输入阻性通口1，两个输出阻性通口2、3，一个弹性通口4。

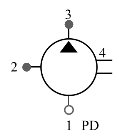
图10.3.21　变排量液压元件模型图标

出口处的质量流量为

泄漏的质量流量为

入口处的质量流量为

式中　W1，W2，W3——液压元件入口处，出口处及泄漏的质量流量（kg／s）；

qmax——液压元件最大排量（m3／r）；

n——液压元件转速（r／min）；

ηv——容积效率；

ε——相对变排量率。

液压元件有两种工作状态，用Swp表示。当（p2－p1）W2≥0时，Swp＝1；当（p2－p1）W1＜0时，Swp＝－1。

当液压元件作为泵工作时（Swp＝1），需要的功率和驱动转矩分别为

当液压元件作为马达工作时（Swp＝－1），输出的功率和转矩分别为

式中　p1，p2——液压元件入口和出口处的压力（Pa）；

η0——总效率。

（2）安全阀（VR）。

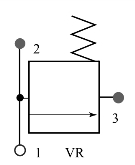
图10.3.22　安全阀模型图标

安全阀模型通过阀口的节流作用，使进口压力等于出口压力，对系统起稳压、安全作用。如图10.3.22所示，该模型为容／阻性元件，有一个输入容性通口1，两个输出阻性通口2、3。安全阀有3种工作状态，用SW表示。

①SW＝0，节流口完全关闭（Af＝0）。

②SW＝1，节流口正在打开或正在关闭（0＜Af＜Amax）。

③SW＝2，节流口完全开启（Af＝Amax）。

安全阀3种工作状态及转换条件如图10.3.23所示。

图10.3.23　安全阀工作状态及转换条件

稳定状态下节流口过流面积为

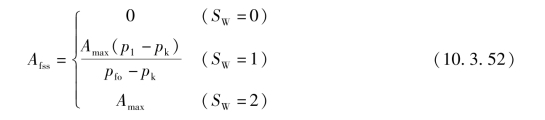
式中　Af，Amax——节流口过流面积和节流口最大过流面积（m2）；

p1，pk，pfo——阀的进口压力，节流口的临界开启压力和完全开启压力（Pa）；节流口过流面积的动态过程用一阶滞后环节考虑，即

式中　tc——动态过程时间常数（s）。

流过节流口的质量流量为

流经阀的出口质量流量为

式中　Cd——流量系数；

p0，p2——阀的节流口出口压力和阀的额定压力（Pa）；

W1——阀的进口质量流量（kg／s）。

（3）节流孔（OV）。

节流孔用来描述液压系统中的节流环节，如压力控制阀通过改变阀口的过流面积来控制出口即可用节流孔描述。节流孔为阻性元件，有两个阻性通口，如图10.3.24所示。压力节流孔有3种工作状态，用SWQ表示。当SWQ＝1时，液体的流动为层流状态；当SWQ＝±2时，液体的流动为紊流状态（±表示方向）。图10.3.25为节流孔工作状态及转换条件。

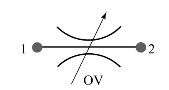
图10.3.24　节流孔模型图标

图10.3.25　节流孔工作状态及转换条件

节流孔的质量流量特性为

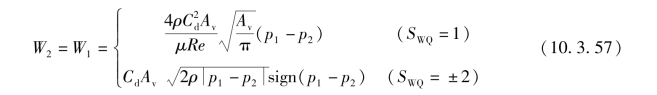
式中　Av——节流孔过流面积（m2），对于圆柱滑阀阀口，Av＝πdv xv；

dv——滑阀直径（m）；

xv——节流孔开度（m）；

μ——动力黏度（Pa·s）；

Re——雷诺数；

p1、p2——节流孔进出口压力（Pa）；

（4）细长孔（LL）。

的小孔称为细长孔，细长孔模型为阻性元件，有两个阻性通口，如图10.3.26所示，其质量流量方程为

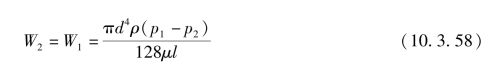
式中　W1，W2——进出口处的质量流量（kg／s）；

p1，p2——进出口处的压力（Pa）；

d，l——细长孔的直径和长度（m）；

（5）质量弹簧（PM）。

压力控制阀、油缸等液压元件的阀芯、活塞等的动态运动过程可用质量弹簧单元描述，该单元受外力、黏性阻力、库仑摩擦力、弹簧力等的作用，是典型的二阶系统。质量块的运动是一非线性过程，需要用基于开－关状态的方程来描述，图10.3.27为模型图标。

图10.3.26　细长孔模型图标

图10.3.27　质量弹簧模型图标

质量块有5种运动状态，用SWP表示，图10.3.28为质量弹簧5种运动状态及转换条件。

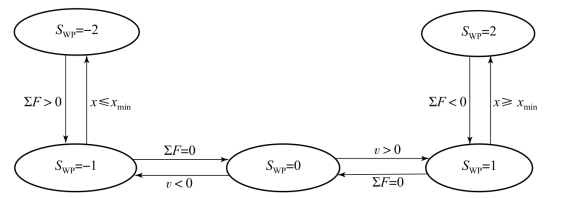
图10.3.28　质量弹簧运动状态及转换条件

①SWP＝－2：x＝xmin＝0，质量弹簧在最小位移处静止。

②SWP＝－1：∑F sign（SWP）＜＜0＆xmin＜x＜xmax，质量弹簧在负的方向运动。

③SWP＝0：∑F＝＝0，质量弹簧在受限处静止。

④SWP＝1：∑F sign（SWP）＜＞0＆xmin＜x＜xmax，质量弹簧在正的方向运动。

⑤SWP＝2：x＝xmax＆x·＝0，质量弹簧在最大位移处静止。

质量块不同的状态动力学方程描述为

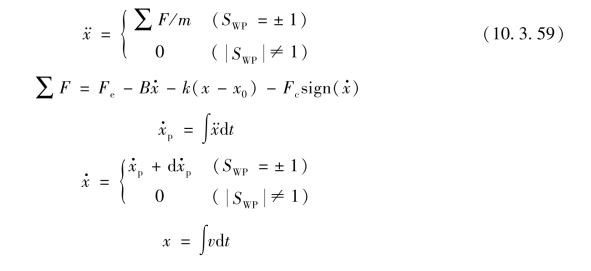
式中　m——质量（kg）；

——质量块加速度（m／s2），速度（m／s）与位移（m）；

xmin，xmax——质量块的最小位移与最大位移（m）；

B——黏性阻尼系数；

k——弹簧刚度（N·m）；

x0——弹簧预压缩量；

Fe——质量块所受外力（N）；

Fc——库仑摩擦力（N）；

——质量块持续的速度状态（m／s）；

——记录质量块受限时瞬态的速度状态。

（6）力计算单元（CV）。

图10.3.29　力计算单元模型图标

力计算单元表示液压系统中液压阀、液压缸容腔内压力对质量块如阀芯、活塞等产生的作用力，图10.3.29为模型图标。

合力单元方程描述为

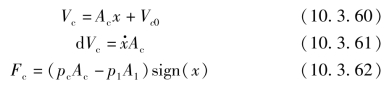
式中　Vc——容腔容积（m3）；

Vc0——容腔初始容积（m3）；

d Vc——容腔容积变化率（m3／s）；

Ac，A1——阀芯或活塞容腔内横截面积与外侧横截面积（m2）；

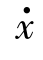，x ——阀芯或活塞运动速度（m／s）与位移（m）；

pc、p1——阀芯或活塞所受容腔内压力与容腔外压力（Pa）；

Fc——阀芯或活塞所受合力（N）。

3）液压控制单元模型

该履带车辆液压控制单元是左、右分配机构，其功用是通过输入信号改变出口压力和进入变速箱相应的液压油缸中油的流动方向，图10.3.30为液压控制系统原理简图，图10.3.31为左、右分配机构压力控制阀模型图标，图10.3.32为内部模型描述。图10.3.32中，TN为回油箱模型；FI为精过滤器模型，是一个容／阻性元件，有一个输入容性通口，一个输出阻性通口；SSS为工作管路模型，是一个容性元件，有一个输入容性通口，两个输出容性通口；OA为过流截面积计算单元；FS为力合成单元；VX为变体积容积单元，是一个容性元件，有两个输入容性通口，两个输出容性通口；LL1为阀芯轴向孔；LL2为压力控制阀出口到离合器液压油缸的管路；SP是一个容／阻性元件，有一个输入容性通口，两个输出阻性通口，分别通向侧变速箱换挡离合器油缸。衬套下腔油压通过作用面积计算单元CV换算成对阀芯底部的作用力、弹簧作用力通过力合成单元FS反馈作用到阀芯PM上，PM的位移通过过流截面积计算单元OA计算出阀口开度，从而控制离合器油缸作用于活塞上的压力。CO为换挡及转向控制器模型。压力控制阀模型有两个信号输入通口1、2（接收换挡信号SR1及转向增压信号SR2），两个阻性输出通口3、4（与离合器液压油缸连接）。

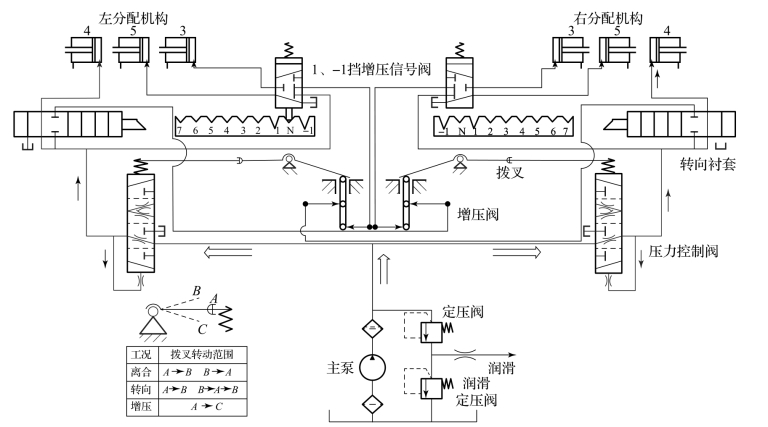
图10.3.30　液压控制系统原理简图

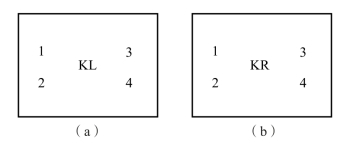
图10.3.31　左、右分配机构压力控制阀模型图标

（a）左分配机构；（b）右分配机构

3.可闭锁式液力变矩器模型（Y）

可闭锁式液力变矩器模型包括闭锁离合器模型（CL）和液力变矩器模型（TC）。闭锁离合器动力学模型参考湿式离合器模型描述，该模型有一个油压信号通口1，与液压控制阀等阻性元件连接，一个输出弹性通口2，给液力变矩器模型提供闭锁力矩。液力变矩器模型有5个惯性通口，其中通口1、2、3、4与轴相连接，通口5与闭锁离合器连接，如图10.3.33所示。

液力变矩器模型中泵轮、涡轮分别被简化成具有惯量的旋转件，其变矩特性由实验测得的原始特性来描述。

为了提高传动效率，对液力变矩器进行闭锁控制。理论上讲，闭锁点应选在偶合器工况点附近，以保证得到较高的传动效率和牵引力。当换挡离合器结合完毕后，变矩器在其传动比满足以下条件时开始闭锁：i≥is。is为变矩器设计闭锁传动比。

闭锁离合器模型始终有nc1＝nB，nc2＝nT。

纯液力工况时有Tc＝0；纯机械工况时有Tc＝TBe，nc1＝nc2。

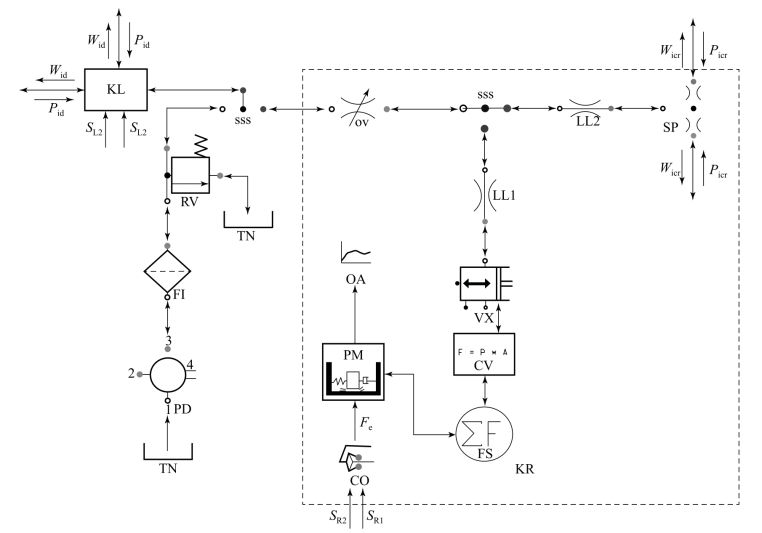
图10.3.32　液压控制系统内部模型描述

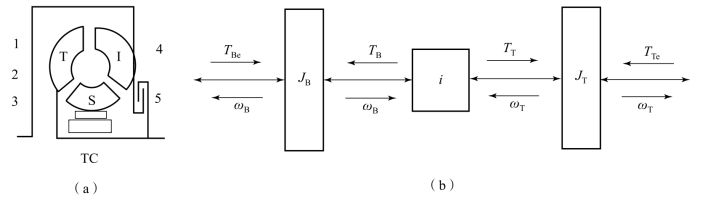
图10.3.33　液力变矩器的动力学模型

（a）模型图标；（b）模型描述

式中　nc1、nc2——闭锁离合器主、被动部分的转速；

Tc——闭锁离合器传递的作用转矩。

图10.3.34为可闭锁式液力变矩器模型，该模型有一个惯性通口1，与发动机相连接；一个弹性通口2，与传动箱输出相连接；一个信号通口3，与闭锁离合器闭锁信号相连接，输入闭锁信号SY。液力变矩器模型的闭锁油压信号是将试验数据以数表的形式输入的。

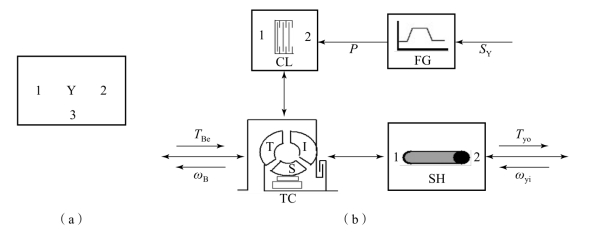
图10.3.34　可闭锁式液力变矩器的模型描述

（a）模型图标；（b）模型描述

所研究的液力机械传动车辆采用的液力变矩器为三工作轮可闭锁式液力变矩器，正透穿型，循环圆直径为D＝0.375 m，设计计算性能为K0＝2.30，λB0＝3.6×10－6。实验原始特性曲线如图10.3.35所示。

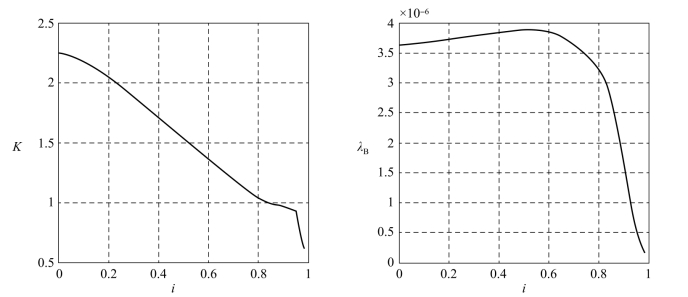
图10.3.35　液力变矩器原始特性曲线

4.传动箱模型

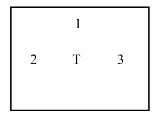
图10.3.36　传动箱模型图标

该履带车辆的传动箱模型主要由一级斜齿轮副和一级锥齿轮副组成。如图10.3.36和图10.3.37所示，该模型有3个功率通口，一个惯性输入通口1，与液力变矩器输出相连接；两个弹性输出通口2、3，与左、右两侧变速箱输入相连接。

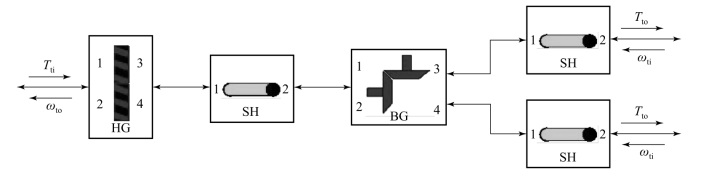
图10.3.37　传动箱内部模型描述

5.行星变速箱模型

该履带车辆的双侧变速箱为三自由度行星变速箱。图10.3.38为侧变速箱传动简图。变速箱由4个行星排和6个操纵件（4个制动器C1、C4、C5、C6和2个离合器C2、C3）组成，有4个运动关系各不相同的行星轮。

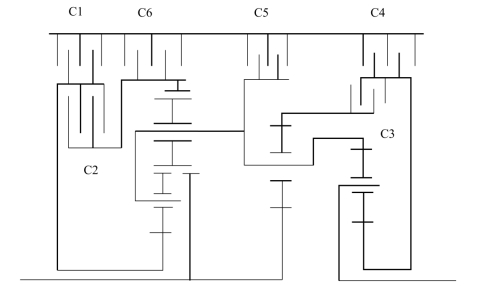
图10.3.38　侧变速箱传动简图

侧变速箱各挡传动比及换挡离合器结合状况如表10.3.2所示。图10.3.39为左、右两侧变速箱模型图标。图10.3.40为侧变速箱内部模型描述。模型中，PG123为1、2、3行星排模型，s1、s2、s3、r1、r2、c1 6个惯性通口，内部模型如图10.3.41所示；CN为轴连接器模型，有8个惯性通口，一个弹性通口。如图10.3.40所示，侧变速箱模型有一个惯性输入通口1，与传动箱输出相连；一个弹性输出通口4，与侧传动输入相连；两个容性输入通口2、3（每一个工况有两个操纵元件结合，因此有两个容性通口），与压力控制阀输出相连。

表10.3.2　侧变速箱各挡传动比及换挡离合器结合状况

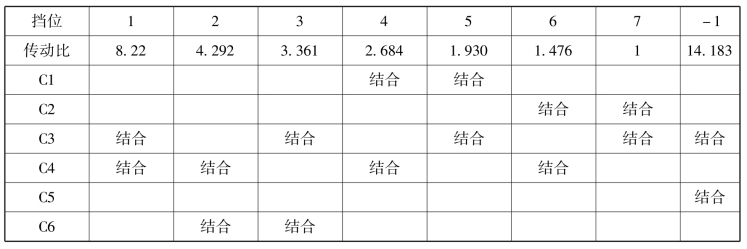
图10.3.39　左、右两侧变速箱模型图标

（a）左侧变速箱；（b）右侧变速箱

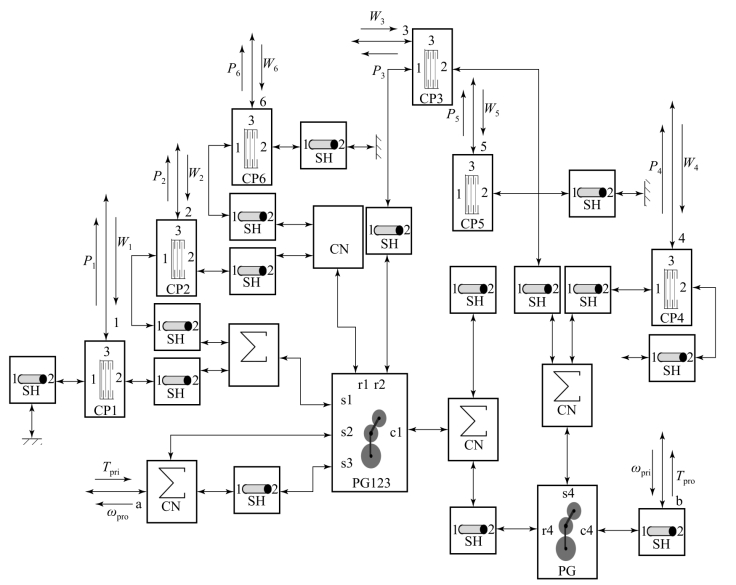
图10.3.40　三自由度行星变速箱内部模型描述

6.侧传动模型

履带车辆动力传动系统的最后一级传动装置为侧减速器，安装于车体两侧的变速箱和主动轮之间。侧减速器主要用来降低前传动传来的转速，增大主动轮上的转矩。它有固定的传动比，可以大大降低前传动转速，提高车辆的通行能力。

该履带车辆侧传动机构为一简单的行星排，太阳轮输入，行星架输出，齿圈固定。如图10.3.42所示，CL、CR分别为左、右侧传动模型。该模型有两个功率通口，一个惯性输入通口1，与左、右侧变速箱输出相连接；一个弹性输出通口2，输出转矩是行动系统主动轮的输入量。

7.传动系统总模型

应用上述可闭锁式液力变矩器模型、传动箱模型、三自由度行星变速箱模型、侧传动模型及液压控制系统模型，可建立如图10.3.43所示的液力机械传动系统模型。由图可知，该模型有8个通口，一个惯性输入通口1，与发动机相连；两个弹性输出通口2、3，与行动部分相连；5个信号输入通口4、5、6、7、8，输入换挡或转向信号。

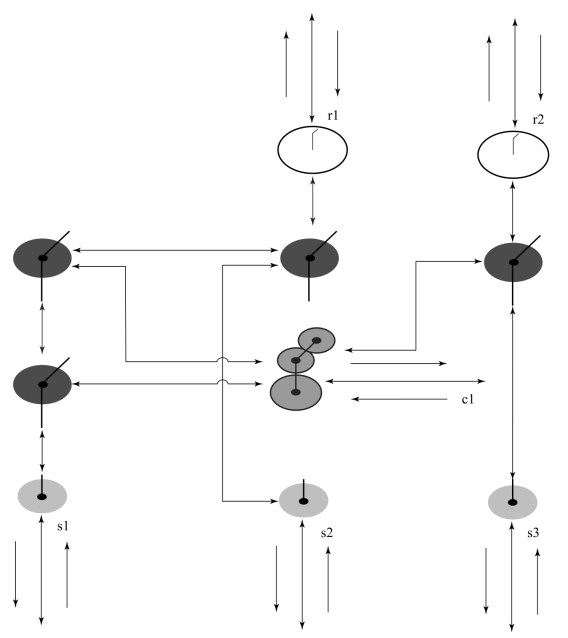
图10.3.41　1、2、3行星排模型

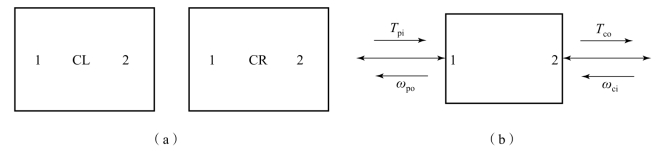
图10.3.42　侧传动模型描述

（a）模型图标；（b）侧传动内部模型描述

图10.3.43　液力机械传动系统模型描述

（a）模型图标；（b）模型描述