车辆通过障碍物的能力不仅取决于障碍物的几何尺寸，也和车辆本身的几何尺寸及重心位置等有关，只有二者适当组合才构成车辆通过的条件。
1.因车身悬起而失去通过性的条件
假设车辆是静止的，沿两个相交平面形成的凸起障碍物运动，那么，障碍平面交点所描出的河点的轨迹如图8.5.2和8.5.3所示，该轨迹理论上是帕斯卡螺线，但可近似地看作一个直径等于Dr的圆，该圆和前、后轮相切。圆Dr和车轮接触的B、C点由角α决定。而α又取决于车辆的极限位置，即当两个车轮正好要从障碍物的一个平面滚入另一个平面的情况。如图8.5.4所示，按照几何关系计算，可得车辆失去通过性的条件为
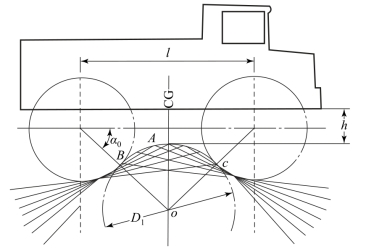
图8.5.2 车辆的纵向地隙
图8.5.3 车辆的横向地隙
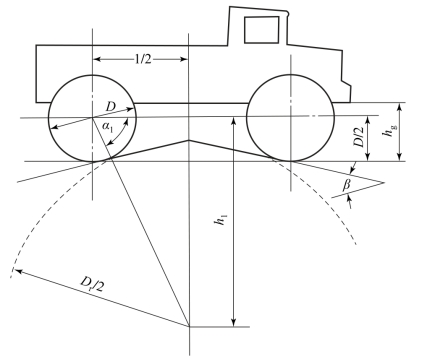
图8.5.4 车辆离地间隙hg与h1的几何关系
2.因车首碰壁而失去通过性的条件
车辆车首碰壁丧失通过性（亦称栽头失效，简称NIF）可能在车辆通过由二、三或四个平面组成的障碍物情况下发生。
图8.5.5表示一台通过两个平面组成的障碍物并驶进沟里的车辆的情况。深为h的沟底和地平面两侧成一角度分别为β1和β，用圆圈代表的车辆前突出部自前轴向前延伸一个距离l1－l。
根据障碍物和车辆的几何关系，NIF发生的条件是
式中 α——车首碰壁时纵轴线的倾斜角。
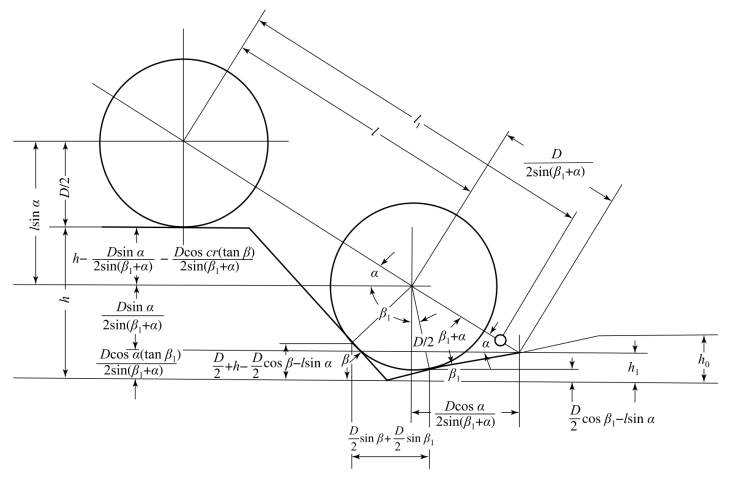
图8.5.5 栽头失效的几何关系
依据几何关系和给定数据可计算出车首突出长度影响通过性的临界条件。
对于由不同数目的平面以不同方式组合的凹形障碍物，可以用上述原理确定相应的NIF条件。
3.车辆超越垂直路障的条件
车辆超越阶状障碍及垂直凸起障碍的性能主要由它们所能克服的垂直障碍的高度来评定，现以履带车辆通过崖壁为例进行越障计算。
凡接近90°的陡上坡均称为崖壁式障碍。崖壁之所以成为障碍，是由于壁面垂直地面，坦克通过时，可能由于产生严重撞击或颠震而损伤机件或人员；或由于发动机牵引力不足而使发动机熄火；或由于附着力不足而使履带打滑，造成坦克不能通过崖壁。
坦克通过崖壁的过程分攀登、通过和落地3个阶段。
1）攀登阶段
攀登阶段指从坦克前轮接触崖壁到前轮轴心搭上崖壁棱沿的过程。
攀登阶段中，坦克车体有两种运动，即车体向前平移和车体的旋转运动，其受力如图8.5.6所示。
此时，作用在坦克上的外力如下。
（1）重力G。它作用在车辆重心C点，垂直于水平面。
（2）壁崖底部地面法向反作用力FN。它作用在履带后端A点，垂直于地面。
（3）牵引力F。作用在A点，与坦克运动方向相同，大小由发动机牵引力、附着力和阻力大小确定，一般情况由地面附着力来确定，即F＝φFN，φ是崖壁底部地面的附着系数，FN的大小代表了攀登阶段坦克在崖壁底部地面上的的附着重力。
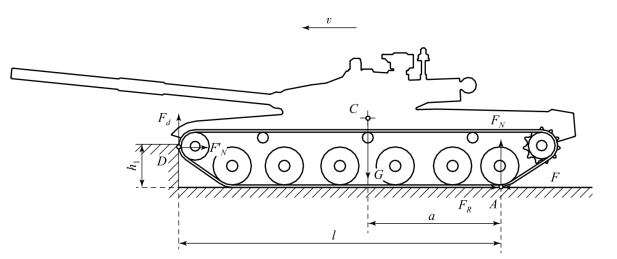
图8.5.6 攀登阶段受力图
（4）行驶阻力FR。它作用在下支履带A点，与坦克运动方向相反，其大小为FR＝fN，f是崖壁底部地面的行驶阻力系数。
（5）壁面法向反作用力F′N。在攀登阶段，坦克前支履带顶住崖壁并给壁面施加一个正压力，壁面会产生一个垂直于壁面的法向反作用力，作用在履带和壁面接触的D点。它与坦克运动方向相反，其大小等于牵引力F和运动阻力FR之差，即
（6）壁面的切向反作用力Fd（攀登力）。其大小为
式中 φ′——壁面附着系数；
f′——壁面的行驶阻力系数。
在攀登阶段，此力的方向可能朝上，也可能朝下。只有Fd向上时，才叫攀登力，这时，车辆才有可能克服崖壁。所以下面就来分析这个反作用力朝上的条件，也就是能够产生攀登力的条件。
在前支履带与壁面接触的D点，要想获得向上的切向反作用力Fd（攀登力），则D点履带在壁面上的绝对速度υjD必须向下。也就是说，只有履带在D点打滑（相对壁面向下滑动），壁面才有可能提供给履带一个向上的切向反作用力。利用履带直驶运动学可以分析D点履带打滑的条件。
如图8.5.7所示，坦克在攀登阶段必须绕某点转动才能使车头向上完成攀登过程。从图中D点和A点分别作地面和壁面的垂直线，两垂线的交点M就是攀登阶段坦克旋转运动的瞬时转向中心。
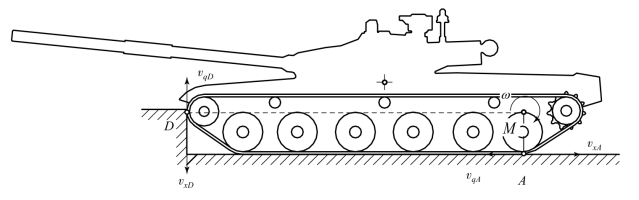
图8.5.7 攀登阶段崖壁和地面与履带接触部分的速度分析
设坦克旋转运动的的角速度为ω，则D点和A点的履带牵连速度分别为
υqD＝ω·MD；υqA＝ω·MA
因为MD＞MA，所以υqD＞υqA。
D点和A点的履带相对速度均相等，即υxD＞υxA，则两点处履带的绝对速度可以表示为
υjD＝υqD－υxD；υjA＝υqA－υxA
要使履带在D点打滑（相对壁面向下滑动），即υjD＜0。就必须满足
υxD＞υqD
也就是
υxA＝υxD＞υqD＞υqA
可见，此时履带在A点必须首先开始打滑（滑转），即υxA＞υqA，υjA＜0。而且，只有在A点滑转到了一定程度之后，D点才开始打滑。下面就来分析D点发生滑转的瞬时，履带在A点的滑转程度，即滑转率的大小。
D点将要发生滑转的瞬时实际上处于理论行驶状态，此时υqD＝υxD＝υxA。根据滑转率的定义可以推导出如下表达式：
上式说明，在D点将要发生滑转的瞬时，履带在A点的滑转率等于1－MA／MD。要使履带在D点产生一定的滑转，履带在A点的滑转率必须满足
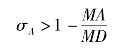(www.xing528.com)
综上所述，在攀登阶段，要想在前支履带与壁面的接触的D点上获得向上的攀登力，在崖壁底部地面支承点上的履带必须滑转，且滑转率必须大于1－MA／MD。
但仅当壁面的切向反作用力Fb朝上，尚不能完全确定坦克履带前端能否搭上崖壁棱沿，还要依据各外力对A点取力矩平衡关系确定，也就是需要满足
式中 h1——D点到A点的垂直高度；
l——D点到A点的水平长度；
a——重心C至A点的水平距离。
否则，不是由于发动机牵引力不足，发动机熄火；就是履带打滑、前轮不能搭上崖壁棱沿。
因此，影响完成攀登阶段的因素主要是牵引力（发动机牵引力和附着力），前轮中心距地高度、车体长、重心位置和崖壁底部及壁面的土壤条件。牵引力F越大，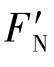
、Fb也就大，越容易完成攀登阶段；前轮中心距地高度h1越高、车体l越长，重心偏后（a小），也越容易完成攀登阶段；φ－f和φ′－f′越大，也越容易完成攀登阶段。
经验证明，h1＝0.7～0.75 m的坦克，依靠履带打滑可以克服的垂直壁高度为0.9～0.95 m。
2）通过阶段
通过阶段是指从前轮轴心搭上崖壁棱沿到坦克重力作用线与崖壁棱沿重合的过程。
通过坦克是坦克能否通过崖壁的关键性阶段，此时坦克受力情况相当于纯上坡直线运动时的受力，如图8.5.8所示，不同之处在于通过阶段中车体与壁底面的夹角随着坦克向上运动而逐渐增大。
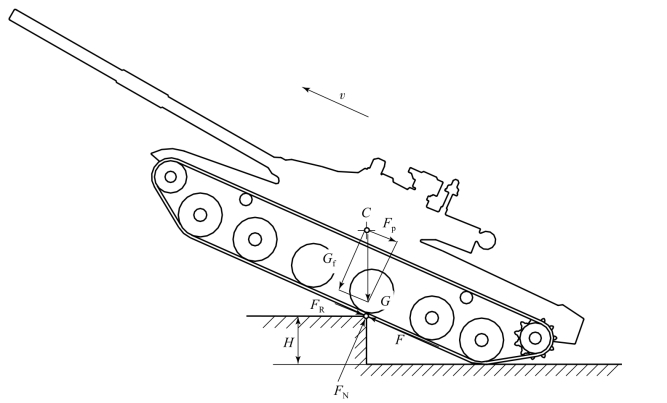
图8.5.8 通过阶段受力分析
当重力作用线与壁面的棱线重合时，其夹角最大，上坡阻力Fp也越大。此时，可能由于发动机牵引力不足而熄火；或由于附着力不足而履带打滑，不能完成这一阶段。
从图8.5.9看出，这阶段坦克能克服的崖高为
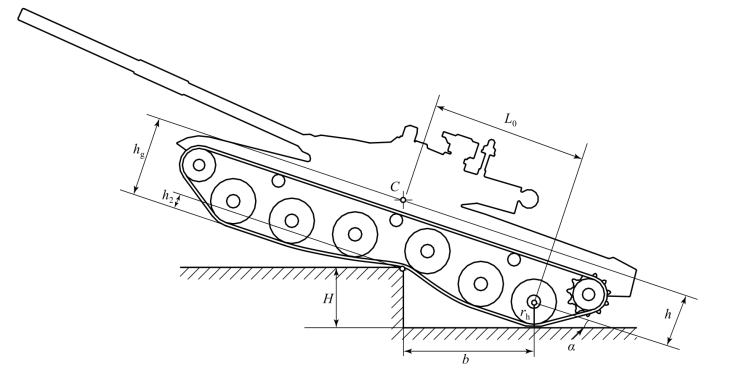
图8.5.9 坦克通过崖壁高度的计算
式中 H——通过崖壁的高度；
L0——坦克重心至后轮轴心的纵向距离；
α——坦克的最大上坡角；
h——平地时重心至后轮轴心的垂直距离；
h2——负重轮的行程；
rh——负重轮的半径；
hg——车辆重心距地高度。
例如，若取l0＝3 m；α＝30°；h＝0.6 m；h2＝0.1 m；rh＝0.3 m；hg＝1.4 m，则可以求出通过崖壁的高度为
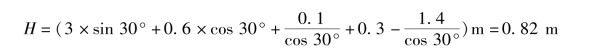
由上式可知，L0愈长，则坦克可能克服的垂直壁愈高，坦克的倾斜角α对克服垂直壁的高度也有影响。若α＝30°～35°，就已接近于所能克服的最大坡度值。一般说来，坦克能克服垂直壁的高度不是受攀登阶段的限制，而是主要受通过阶段的限制。
3）落地阶段
落地阶段指从重力作用线越过崖壁棱线到坦克落于崖壁顶上的过程。在此阶段中，由于坦克的重力作用线越过棱线时，形成一个向下转动的力矩，使坦克落于崖壁顶部。正确通过此阶段的主要标志是坦克下落时颠震小，不倒滑下来。若此时车速高，则造成颠震就严重，可能摔坏机件或人员；若减油早，牵引力不足则会使车辆滑下来或倒爆。因此，当坦克重心越过垂直壁开始下落时，必须停止供油，有时还要制动，使坦克慢慢地落于崖壁顶上。
4.车辆通过壕沟的条件
轮式车辆所能克服的壕沟宽度在很大程度上取决于车轮直径和轴距等几何参数，因此，轮式车辆跨越壕沟的性能也和超越垂直障碍物的情况一样，可以用壕沟宽度ld与车轮直径D之比ld／D来评定。贝克认为，对同一轮式车辆来说，所能克服的垂直障碍高度与车轮直径之比h／D可以和ld／D相互转换，如图8.5.10所示。因此，若已知h，就可按图中曲线确定ld。
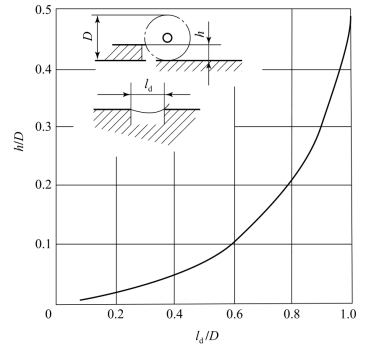
图8.5.10 h／D和ld／D的关系曲线
坦克通过壕沟的宽度与坦克的车长、重心位置以及驾驶方法有关。克服壕沟可以用静力法（即坦克缓慢行驶）和动力法（坦克高速行驶，利用动能来克服壕沟）。
坦克的越壕宽是指坦克以低速法通过平地壕沟时，头部或尾部不掉入沟内的最大宽度。
用静力法克服壕沟受坦克稳定性丧失的限制。稳定性的丧失是在坦克的重力作用线超出负重面的界限的情况下发生。如果重力作用线是在车首和对面的壕壁接触之前超出负重面的，那么坦克的前部就落入壕中；如果重力作用线还未到达对面的壕壁，而坦克的尾部已和第一壁脱离，那么坦克的尾部就落入壕内。
所以，用静力法克服壕沟的可能性取决于坦克两端支撑点和坦克重心在行驶平面上的投影间的距离，如图8.5.11所示。若取主动轮和诱导轮轴心为两端支撑点，则坦克可能克服的最大壕宽应等于a和b中的较小值。
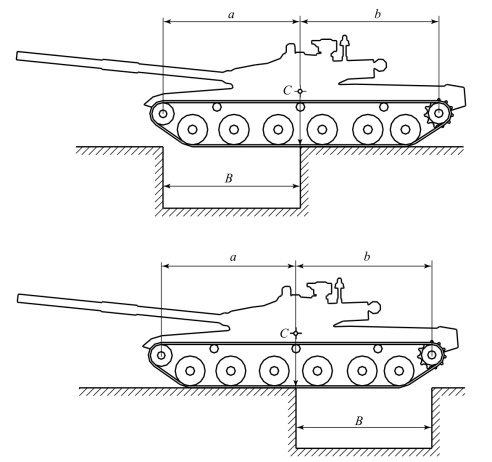
图8.5.11 坦克以静力法通过水平地面上的壕沟
如果企图克服宽为B＝b，且a＜b的壕沟时，当坦克前端尚未支撑在壕沟前缘时，坦克重心就早已离开壕沟后缘，于是坦克前端就落入壕沟中。
如果企图克服宽为B＝b，且a＜b的壕沟时，当坦克尾部已失去壕沟后缘的支撑时，坦克重心尚未靠近壕沟前缘，于是坦克尾端就落入壕沟中。
现代的中型和重型坦克，当其两端支撑点长a＋b＝5～6 m，重心差不多位于履带接地段的中间时，用静力法所能克服的壕沟宽B为2.5～2.8 m。
为了能克服较宽的壕沟，在设计坦克时应尽量将其重心布置在履带接地段中心处。
用动力法克服壕沟就是以较高的速度驶过壕沟，这样可以增加越壕的宽度。在坦克高速通过壕沟时，当第一负重轮脱离支持面后，车体便开始向沟底下倾。显然，如果坦克的行驶速度越高，在同一距离内，坦克车体前部向沟底下落的程度便越小。
应用动力法克服壕沟与壕沟两边缘的相互位置和形状有很大关系，如果壕沟的前边缘比后边缘高则难以克服，反之则较容易克服。如果后边缘呈下坡的斜面，则不易通过；如呈上坡状斜面，则较易克服。
应用动力法克服壕沟虽然可以提高越壕的宽度，但必须注意壕沟前沿的地面状态、乘员的安全和机件的损坏，所以，一般不用动力法越壕。当壕沟前沿是木质的、石头的或冻结的地面时，为了避免撞击力对乘员的安全和行驶装置的损坏，亦不宜采用动力法。当坦克通过宽度为车体长30%～45%，而且边缘坚固的壕沟时，应挂低速挡通过。
坦克在上坡克服壕沟的第一阶段（即坦克前端跨过壕沟的时候）与克服水平地段上的壕沟比起来，坦克重心是不容易超过后边缘的，如图8.5.12所示。因此，就第一阶段来说，坦克能克服的壕宽为
B＝a＋hg tanα
式中 α——上坡坡度角；
hg——坦克重心高度。
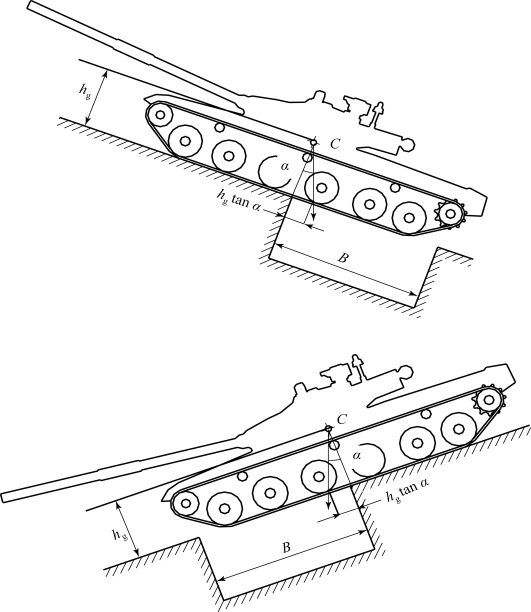
图8.5.12 坦克在上、下坡时克服壕沟
可是在第二阶段，坦克尾端跨过壕沟时，坦克可以克服的壕宽将减为
B＝b－hg tanα
所以，坦克在上坡时克服壕宽较在水平地段上要小。同理，坦克在下坡时第一阶段能克服的壕宽较平地时要减小，所以下坡克服壕宽较在水平地段上也要小。
例如，坦克重心高度hg＝0.9～1.2 m，坡度角α＝30°时，则在上、下坡时所能克服的壕宽，将比水平地段时减少hg tanα＝（0.9～1.2）×0.578 m。
如果坦克的几何形状和障碍物的几何形状能够保证坦克和地面间必要的间隙，加上足够的牵引力和附着力，地面的几何障碍是可以越过的。但是，对于不可越过的障碍，如水、树木和山，坦克的几何形状能起的作用很小，而前进到目的地的唯一办法是绕过障碍，这就使得行程增加，坦克的运行速度降低。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
