接地压力分布对牵引力的影响：车辆系统仿真理论与实践成果

前面我们分析了当履带接地压力均匀分布时土的推进力（即履带车辆的切线牵引力），实际上履带接地压力的分布很少是均匀的，为此，有必要研究履带接地压力分布规律对牵引力的影响。下面从3种典型的履带接地压力分布规律着手，论述履带车辆接地压力分布规律对牵引力的影响。

1.履带接地压力中心偏前

由于车辆的质心布置和工作装置结构等原因，履带接地压力中心可能偏前。现假设一极端情况，即E＝－L／6，并假设履带接地压力沿接地长度呈线性分布（见图8.3.3），则有

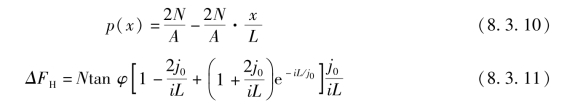
式中　N——土的法向反力。

履带接地压力中心偏前将使车辆切线牵引力降低，当E＝－L／6时，降低值为ΔFH。

2.履带接地压力中心偏后

由于上述同样的原因，履带接地压力中心也可能偏后。现假设为另一极端情况，即E＝L／6，并假设履带接地压力沿接地长度呈线性分布（见图8.3.4），则有

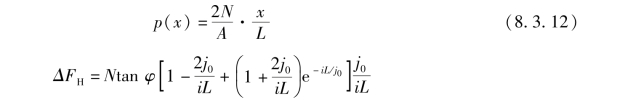
根据上式可得出结论，履带接地压力中心偏后可增加车辆的切线牵引力，当E＝L／6时，增大值也为ΔFH。

图8.3.3　接地压力中心偏前示意图

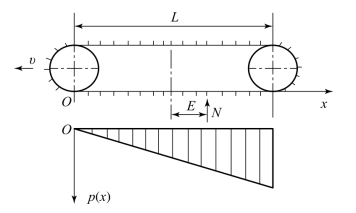
图8.3.4　接地压力中心偏后示意图

3.履带接地压力非线性分布

当车辆的履带装置支重轮数量较少时，履带接地压力可视为非线性分布。

为了简化计算，特作以下假定：①履带接地长度范围内，支重轮呈等距离分布；②E＝0；③履带接地压力分布规律为一多峰余弦函数，并于支重轮下方产生峰值，如图8.3.5所示。

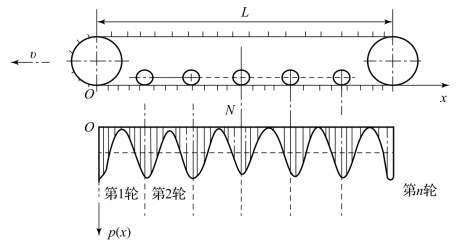
图8.3.5　接地压力非线性分布示意图

基于上述假定，可建立履带接地压力分布函数，即

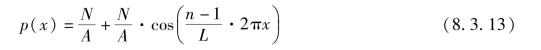
式中　n——接地车轮的个数，即支重轮个数加2。

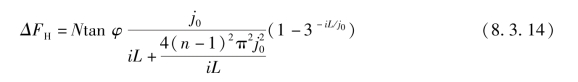
根据式（8.3.14）可得出结论：履带接地压力呈多峰余弦函数分布，将使车辆切线牵引力降低，在所述条件下，降低值为ΔFH。

4.具有横向偏心距(www.xing528.com)

若车辆重心具有横向偏心距C，假设纵向偏心距为0，则两侧履带接地压力将不同，牵引力也会不同。则有

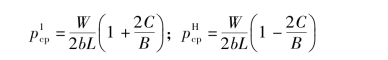
那么，两条履带牵引力之差为

当车辆重心（考虑垂直外载荷时为接地压力中心）具有横向偏心距C时，整机的牵引力不受影响，但两条履带各自的牵引力不等，有一差值ΔFH12，该差值与C成正比，与轨距B成反比。若C／B较大时，则差值较大，将导致车辆在直线行驶时，产生“偏载”或“跑偏”现象，这样就增加了车辆单条履带的磨损。因此，车辆重心的横向偏心距C对履带行走装置的使用寿命是很不利的，设计时，要尽量将其压缩到最低限度。

5.履带接地压力为不连续三角形分布

履带下的接地压力可以近似地看成不连续的三角形分布，其最大压力值位于各支重轮的正下方，如图8.3.6所示。

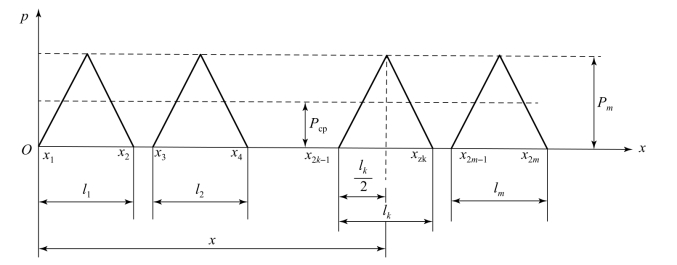
图8.3.6　不连续的三角形分布的接地压力示意图

计算三角形顶点的动平均接地压力Pm的公式为

式中　pm——三角形顶点的峰值压力；

pcp——名义平均接地压力（或静载平均接地压力）；

I——动载荷系数；

lk——同时受到一个支重轮负荷的履带板长度；

L——履带接地长度；

k——支重轮的序数，k＝1，2，3，…。

现取任意一个三角形，分析其压力分布变化规律。由图8.3.6可知，在三角形左侧，压力p随x的增加而增大，直到顶点的最大值；在三角形右侧，压力p随x的增大而减小，直到减为零。根据相似三角形原理，左侧压力分布函数为

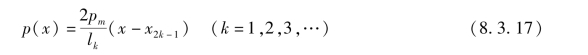
右侧压力分布函数为

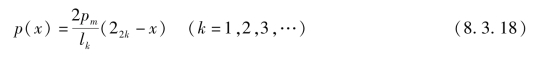
分别用p（x）代替p，依据式（8.1.2）和式（8.1.3）分别计算出两种土壤的剪切应力τ（x），最后利用下式计算整条履带的牵引力：

其中，τ（x）由土的参数和p（x）而求得，但p（x）必须分两段代入。