稳态计算模型：汽车系统仿真实践

典型车用大功率柴油机结构如图7.5.1所示。在保证动力性的前提下，为了提高柴油机的紧凑程度，通常采用V型结构和废气涡轮增压加中冷的技术方案。柴油机工作时，新鲜空气首先经压气机压缩以提高进气密度；从压气机流出的空气经中冷器冷却，进一步提高密度后流入进气管；进气管中的新鲜空气在进气门开启时流入气缸，与燃油混合燃烧后产生的废气经排气门流入排气系统；涡轮从废气中回收能量，用以驱动压气机工作。

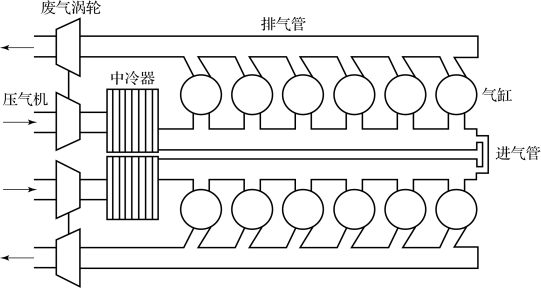
图7.5.1　车用大功率柴油机结构示意图

废气涡轮增压柴油机是一个复杂的热力系统，在模拟其工作过程时，为了使结果更符合实际，需要综合考虑气缸内热力过程（燃烧、换气、传热等）、进排气管路气体流动，以及调速器、喷油泵、压气机、废气涡轮、中冷器等典型部件的工作。

1.气缸内热力过程模型

将气缸盖底面、活塞顶面和气缸套内壁面围成的空间作为一个热力系统，通常采用“容积法”计算其内的热力过程，描述工质状态的参数有压力、温度、质量和组成成分，它们由能量守恒方程、质量守恒方程及气体状态方程联系起来，经联立求解后得到工质状态参数随曲轴转角的变化。

为此，需要作如下简化假设：

（1）气缸内的状态是均匀的，也就是不考虑气缸内各点的温度、压力和浓度的差异，并认为在进气期间，流入气缸内的空气与气缸内的残余废气实现瞬时的完全混合；

（2）气缸内工质为理想气体，其比热、内能仅与气体温度和气体成分有关；

（3）气体流入或流出气缸为准稳定流动；

（4）进、出口的动能忽略不计。

由气缸内热力系统能量守恒，得气缸内温度变化微分方程为

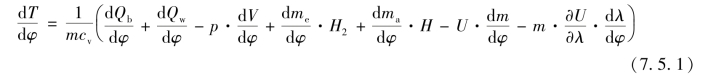
由气缸内热力系统质量守恒，得气缸内质量变化微分方程为

理想气体状态方程为

式中　m——气缸内气体质量（kg）；

p——气缸内气体压力（Pa）；

V——气缸内气体体积（m3）；

T——气缸内气体温度（K），1 K＝－272.15℃；

λ——过量空气系数；

cv——气体定容比热（J／（kg·K））；

U——气缸内单位质量气体对应的内能（J／kg）；

H——气缸内单位质量气体对应的焓（J／kg）；

H2——流入气缸单位质量气体对应的焓（J／kg）；

dme／dφ——流经进气门的气体质量随曲轴转角的变化率（kg／°CA）；

dma／dφ——流经排气门的气体质量随曲轴转角的变化率（kg／°CA）；

dmb／dφ——气缸内燃油质量随曲轴转角的变化率（kg／°CA）；

dQb／dφ——燃料燃烧放热率（J／°CA）；

dQw／dφ——气缸壁面传热率（J／°CA）。

1）气缸内燃烧模型

通常采用零维模型模拟气缸内燃烧过程，即用（单、双、三）韦伯燃烧函数模拟气缸内燃烧放热率及瞬时燃料质量变化率。

采用三韦伯燃烧函数计算柴油机燃烧放热率的计算公式为

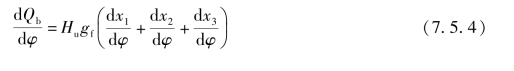
式中　Hu——柴油低热值；

gf——单缸循环供油量；

dx1／dφ——预混合燃烧中已燃燃料份数随曲轴转角的变化率；

dx2／dφ——主燃烧中已燃燃料份数随曲轴转角的变化率；

dx3／dφ——尾燃烧中已燃燃料份数随曲轴转角的变化率。

令

则有

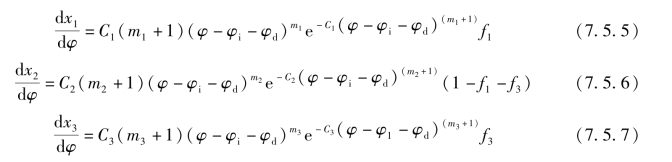
式中　φi——喷油开始角；

φd——燃烧延迟角；

f1——预混合燃烧份数；

f2——主燃烧份数；

f3——尾燃烧份数；

m1——预混合燃烧品质指数；

m2——主燃烧品质指数；

m3——尾燃烧品质指数；

Δφ1——预混合燃烧持续角；

Δφ2——主燃烧持续角；

Δφ3——尾燃烧持续角。

由三韦伯燃烧函数确定的瞬时燃烧放热率曲线和累积燃烧放热率曲线分别如图7.5.2和图7.5.3所示。

由燃烧放热率可以计算气缸内燃油质量变化率，计算公式为

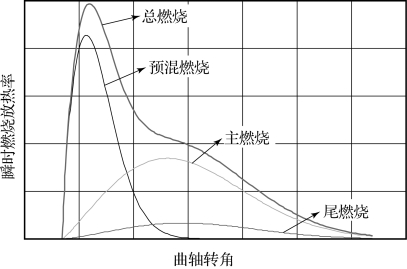
图7.5.2　三韦伯燃烧函数瞬时放热率曲线

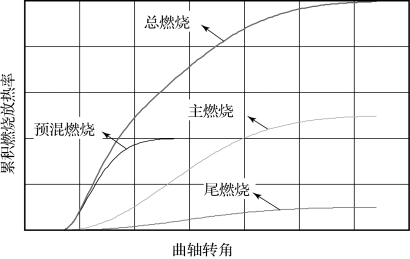
图7.5.3　三韦伯燃烧函数累积放热率曲线

在模拟气缸内热力过程时，需要合理确定燃烧延迟时间ti（燃烧开始角θz），其方法是从实际喷油开始（实际喷油开始角等于几何喷油开始角与喷油延迟角之和），在每一计算步长之内，计算燃烧延迟时间ti并求s＝∑dφ／ti，dφ为计算步长。当s≥1时即认为开始燃烧。可根据气缸内瞬时温度和压力计算燃烧延迟时间，计算公式为

2）气缸壁传热模型

气缸壁面传热按活塞顶面、气缸盖底面和气缸套内壁面3个部分计算，计算公式为

式中　ω——发动机曲轴转动角速度；

Twi——气缸壁面温度；

Ai——气缸壁传热面积；

αwi——气缸壁传热系数，可以用Woschni公式计算，计算公式为

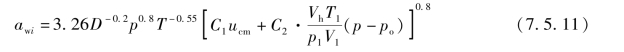
式中　ucm——活塞平均运动速度（m／s）；

po——倒拖工况对应的气缸压力（kPa）；

T1——压缩始点的气缸内燃气温度（K）；

p1——压缩始点的气缸内燃气压力（kPa）；

T——气缸内气体温度（K）；

p——气缸内气体压力（kPa）；

V1——压缩始点的气缸容积（m3）；

Vh——气缸工作容积（m3）；

D——气缸直径（m）；

C1——气体速度系数；

C2——燃烧室形状系数。

气体速度系数由气缸所处的工作阶段、进气涡流速度和活塞平均速度确定。

换气过程

C1＝6.18＋0.417uu／ucm

压缩、燃烧和膨胀过程

C＝2.28＋0.308u／u1ucm

式中　uu——进气涡流速度（m／s）。

换气和压缩过程

C2＝0

燃烧和膨胀过程

C＝0.003 24（直喷式），C＝0.006 22（预燃式）22

3）换气过程模型

换气过程中，流入、流出气缸的气体质量随曲轴转角的变化率按瞬时质量流量计算，计算公式为

式中　——流经排气门的气体瞬时质量流量。

气体流经排气门时准稳定流动处理，其理论流量按一维等熵流的流量公式计算，实际流量等于理论流量乘以流量系数，即

式中　ψ——流动函数；

μ——流量系数；

A——瞬时流动面积；

pI——气门入口气体压力；

ρI——气门入口气体密度。

若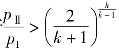，则为亚临界流动，有

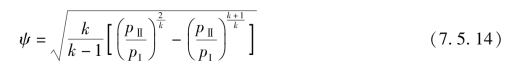
若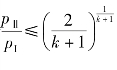，则为超临界流动，有

式（7.5.14）、式（7.5.15）中，下标号Ⅰ、Ⅱ分别表示气门入口、出口。

流量系数μ采用下式计算，即

式中　h——气门瞬时升程；

d——气门直径。

2.进排气管路气体流动模型

进排气管路内的气体通常做有摩擦、有传热的一维非定常流动处理，可采用“有限容积法”计算其热力参数及流动状态。

如图7.5.4所示，“有限容积法”将计算区域划分为有限个、连续、无重叠的容积，在每个容积内应用控制方程的守恒形式，得到代数方程。计算节点位于容积内部，边界上的值由相邻节点上的变量插值得到，这样就可以在每个控制体内得到一个以本节点和若干个相邻节点变量表示的方程组，补充相应的边界条件使方程组封闭，这样求解与节点数相同的方程组就可以得到整个计算区域的解。

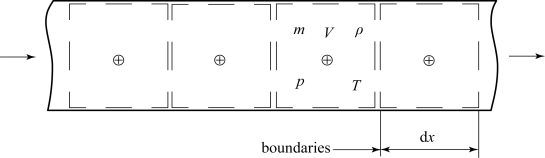
图7.5.4　管道系统内的容积划分

对于构成进排气系统的管道和三通部件，需要求解描述其内部气体流动的连续方程、能量方程和动量方程。

连续方程为

能量方程为

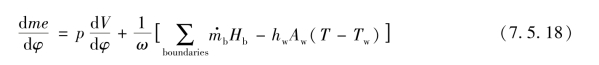
动量方程为

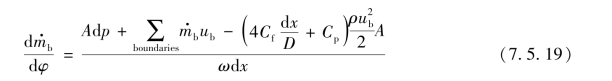
式中　φ——曲轴转角（°CA）；

ω——曲轴旋转角速度（°CA／s）；

m——气体质量（kg）；

ρ——气体密度（m3／s）；

p——气体压力（Pa）；

V——气体体积（m3）；

T——气体温度（K）；

e——单位质量气体的总能量，包括气体内能和动能（J／kg）；

A——气体流动截面积（m2）；

D——气体流动截面的当量直径（m）；

ub——边界面处的气体流速（m／s）；

——边界面处的气体质量流量（kg／s）；

Hb——边界面处单位质量气体对应的总焓（J／kg）；

Aw——壁面传热面积（m2）；

Tw——壁面温度（K）；

hw——壁面传热系数（W·K·m－2）；

Cf——壁面摩擦系数；

Cp——压力损失系数；

dx——沿气体流动方向的气体厚度（m）；

dp——dx对应的压力降（Pa）。

气体沿管道壁面流过时，会造成压力损失，对应的壁面摩擦系数可以根据气体流动状态和管道尺寸确定。

对于光滑管道，壁面摩擦系数由下式决定：

对于粗糙管道，壁面摩擦系数由式（7.5.20）和下式共同决定：

(www.xing528.com)

式中　Re——气体流动的雷诺数；

D——管道当量直径（m）；

h——管道壁面粗糙度（m）。

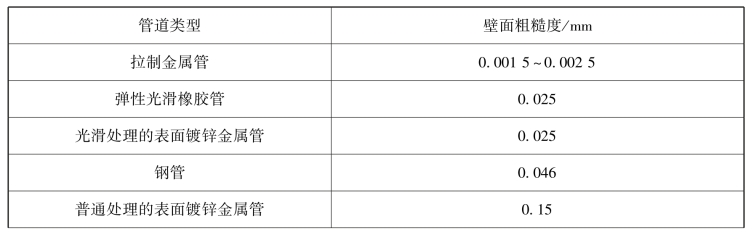
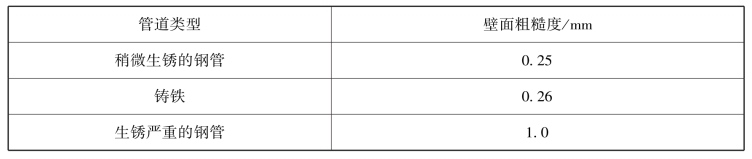
不同类型管道的壁面粗糙度如表7.5.1所示。

表7.5.1　不同类型管道壁的壁面粗糙度

续表

3.部件工作模型

1）调速器

调速器的作用是根据柴油机外界负荷变化自动控制供油量。对全程式调速器来说，其作用具体表现为，限制发动机最高空转转速；稳定发动机最低空转转速；当外界负荷发生变化时，自动调节供油量，使发动机在一定转速范围内稳定工作。

若为电子调速器，则可根据调速器调速特性实验数据描述其工作过程，即

式中　n——发动机转速；

Th——油门开度。

若为机械调速器，则可根据调速结构与工作原理建立描述其工作的数学模型。

常见的机械调速器有飞球离心式机械全程调速器和可变杠杆比机械全程调速器（简称RQV调速器，“R”表示离心式调速器，“Q”表示用操纵杆改变浮动杠杆比，“V”表示全程调速器）两种，对应结构分别如图7.5.5和图7.5.6所示。

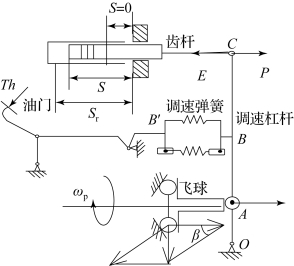
图7.5.5　飞球离心式机械全程调速器结构示意图

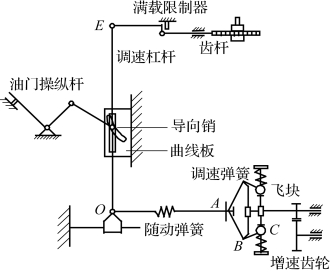
图7.5.6　RQV调速器结构示意图

对于飞球离心式机械全程调速器，飞球作为感应元件。在某一个稳定工况下，作用在齿杆上的力有两个，一个是弹子离心力换算到齿杆处的称为支持力P，另一个是弹簧拉力换算到齿杆处的称为恢复力E，这两个力互相平衡。当驾驶员操纵油门位置时，E增大，使齿杆向加油方向移动，内燃机扭矩增大，调速器轴角速度增大，使P增大，二者在经过过渡工况以后最终达到新平衡。同样，在外界负荷增大时，调速器轴角速度将减小，P减小，此时E＞P，齿杆向加油方向移动，内燃机扭矩增大，最终E与P达到新的平衡。

对于RQV调速器，当柴油机稳定工作时，调速器飞块离心力和弹簧支持力相互平衡，加油齿杆位置一定，供油量保持不变。当外界负荷变化时，柴油机转速随之变化，导致飞块离心力变化，从而破坏了它和调速弹簧的平衡，使得飞块移动并通过角形杠杆（ABC）、伸缩轴（OA）、滑套（O）使调速杠杆（OE）以导向销为支点转动，从而带动齿杆移动改变供油量，直到和负荷重新相适应为止。此时，柴油机在一新的转速稳定。当在柴油机初始稳定工作的基础上突然将油门操纵杆转到另一位置后固定不变，则扳动油门操纵杆的瞬间，调节杠杆以其下端为支点摆动并带动齿杆移动，从而破坏柴油机的平衡；飞块感受转速的变化并通过角形杠杆使滑套移动；由于油门操纵杆位置不再改变，导向销受到传动杆和曲线板的约束也不能移动，因此调节杠杆以导向销为支点转动并带动齿杆移动，直到齿杆重新回到供油量与负荷相适应的位置，柴油机和调速器在新的状态下达到平衡。

假设调速器稳定工作时油门位置为Th，杠杆比为α，齿杆位移为s，飞块旋转半径为r、离心力为P，弹簧支持力为E，标定工况时齿杆位移为sa，飞块旋转半径为ra。

若调速器未工作时低速弹簧不发生形变，则高低速临界弹力可表示为

式中　kd——低速弹簧刚度（N／m）；

kgw——高速外弹簧刚度（N／m）；

kgn——高速内弹簧刚度（N／m）；

Δzd——低速弹簧单独作用行程（m）；

Δzgw——高速外弹簧预压缩量（m）；

Δzgn——高速内弹簧预压缩量（m）。

此时，飞块离心力为

式中　M——飞块质量（kg）；

ωp——飞块旋转角速度（rad／s）；

rmin——飞块最小旋转半径（m）。

如果P0＜E01，则说明柴油机转速较低，低速弹簧可以单独提供支持力，此时弹簧支持力为

如果P0＞E02，则说明柴油机转速较高，需要高、低速弹簧共同提供支持力，有

飞块离心力为

结合飞块平衡条件E＝P计算飞块旋转半径。

如果P0＜E01，飞块旋转半径为

如果E01≤P0≤E02，飞块旋转半径为

如果P0＞E02，飞块旋转半径为

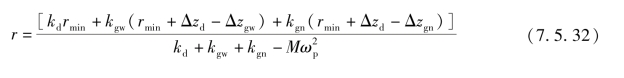
而

式中　ωin——调速器输入转速（rad／s）；

R——调速器齿轮增速比。

若A点相对于飞块旋转平面的距离为z，则由调速器结构上的关系，有

式中　AC——调速器角形杠杆两端点间的距离（m）；

za——标定工况时A点相对于飞块旋转平面的距离（m）。

由式（7.5.34）可得A点相对于标定工况的位移量为

对RQV调速器，随着油门位置的增大，杠杆比随之增大，杠杆比α随油门位置Th变化的两段线性关系式为

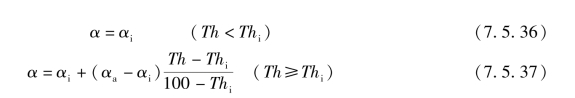
式中　αi——怠速工况对应的杠杆比；

αa——标定工况对应的杠杆比；

Thi——怠速运转油门位置值。

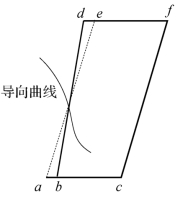
图7.5.7　齿杆与滑套运动关系示意图

如图7.5.7所示，cf、bd分别代表两油门位置时的调节杠杆位置，ae为过导向销位置所作的辅助线，且ae平行cf，认为齿杆沿df做直线运动，滑套沿ac做直线运动，且df平行于ac，则有

df＝de＋ef＝α·ab＋ac

ab＝ac－（z－za）

ac＝sda－sd

df＝sa－s

整理得

即

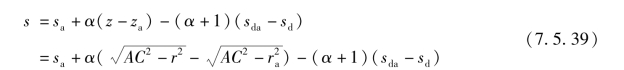
式中　sda——全油门位置时导向销在滑套方向的位移（m）；

sd——部分油门位置时导向销在滑套方向的位移（m）。

根据导向曲线形状，采用相切的两段抛物线关系式确定sd随油门位置的变化关系，具体如下。

令

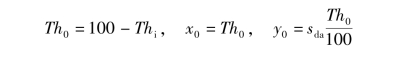
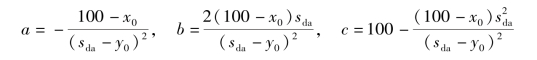
当Th＜x0时

当Th≥x0时

由式（7.5.40）和式（7.5.41）确定的sd可使式（7.5.39）给定的s满足：柴油机转速增加，则r增大，从而导致s减小；油门开度增大则s增大；smin≤s≤smax，若由式（7.5.39）所得的s＞smax，则表示随动弹簧受压；若s＜smin，则表示随动弹簧受拉。smin、smax分别为齿杆最小位移和齿杆最大位移。

2）喷油泵

基于喷油泵供油特性实验数据描述其工作，即

已知发动机转速和加油齿杆位移的情况下，可基于喷油泵供油特性数据插值得到发动机单缸循环供油量，为气缸内燃烧模拟计算提供已知条件。

3）压气机

入口压力为

式中　p0——环境压力；

Δp10——设计工况时压气机前的总压降，一般为100～300 Pa。

压比为

式中　Wk——压气机消耗功；

Gk——压气机循环流量；

T0——环境温度。

出口压力为

出口温度为

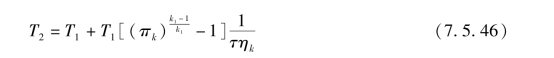
式中　T1——压气机入口气体温度；

τ——考虑向外散热的冷却系数，一般取1.04～1.1。

消耗功率为

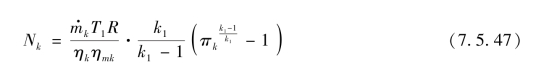
式中　ηmk——压气机机械效率。

计算时需要输入压气机特性，它一般以特性曲线的形式给出。在特性图中，共有压气机流量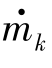、压比πk、转速nk、等熵效率nk 4个参数，而且nk、ηk与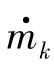、πk有一定的关系，也就是说，nk、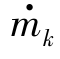及πk或ηk、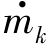及πk 3个参数中的两个参数决定后，第三个参数就确定了。利用这一关系，将压气机特性以数组形式输入计算机，在计算中根据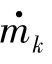与πk从数组中插值求出nk、ηk，相应的两数组形式为

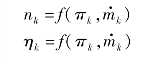
4）废气涡轮

膨胀比为

式中　pB0——涡轮入口处的绝热滞止压力，可由排气总管内的气体状态及流速求出；

p5——涡轮后的静压p5，可按下式计算：

式中　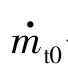——设计工况时的涡轮流量；

Δpt0——涡轮后的压力损失，其最大允许值为2 000～2 500 Pa。

涡轮效率表示涡轮中能量转换的完善程度，主要与速度比u／c0有关，膨胀比πt对它的影响较小，可以忽略不计，即

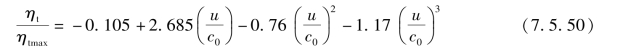
式中　ηtmax——涡轮的最高效率；

u——涡轮叶轮圆周速度；

c0——涡轮喷嘴前燃气速度。

吸收功率为

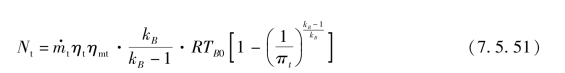
式中　ηmt——涡轮机械效率。

计算时需要涡轮流通特性，即涡轮流量随涡轮膨胀比πt的变化关系，可根据涡轮膨胀比，采用对涡轮流通特性插值的方法求取涡轮流量。

5）中冷器

中冷器可作为一定数量的散热管处理，空气流经中冷器的压力降为

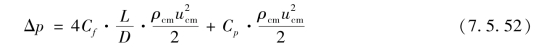
式中　L——管道长度（m）；

D——管道当量直径（m）；

ρcm——空气平均密度（kg／m3）；

ucm——空气平均流速（m／s）；

Cf——壁面摩擦系数；

Cp——压力损失系数。

中冷器出口空气温度可由中冷器效率计算得到，即

式中　ηz——中冷器冷却效率；

Tc——冷却介质进口温度；

T2——压气机出口温度。

4.计算流程

柴油机工作过程稳态计算流程如图7.5.8所示。如果计算发动机调速特性，则直接输入油门开度及发动机转速；如果计算发动机负荷特性，则需要根据所给发动机转速及负荷对油门开度进行迭代计算求取对应油门开度值，其计算流程如图7.5.9所示。

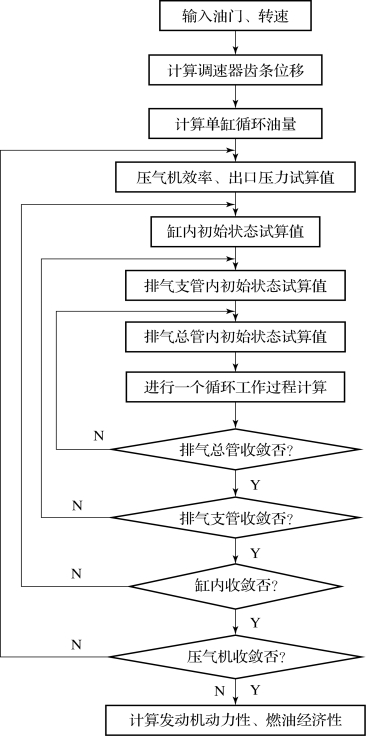
图7.5.8　柴油机工作过程稳态模拟计算流程

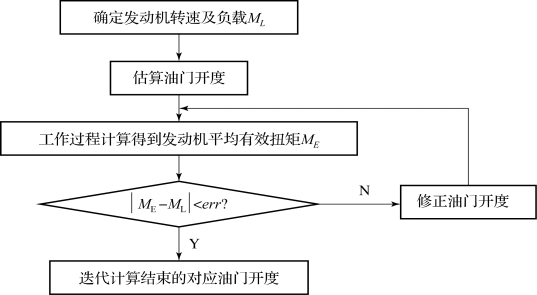
图7.5.9　油门迭代求解流程