车辆系统仿真理论实践结果

1.动态过程及模拟

设计和使用军用履带车辆的特殊性取决于动力传动装置中产生的动态过程特性。动力传动部件具有弹性，在周期性变化的转矩作用下，多个质点运动的瞬时速度不同，产生振动质量本身的惯性力矩和振动质量间的弹性力矩。在这些力矩作用下，系统由静止状态过渡到振动状态。

自由振动是由内部变化的力矩引发的，这些振动的频率由系统的基本参数决定。每一种自由振动对应着一个固定的表达式——振动质量的振幅与连接变形间相互关系的总和。动力传动装置组成的多样性确定了系统中诸多集中质量，现行的各种变速箱具有包括车辆直线和转向行驶传动装置在内相应的不同结构型式。所有这些都确定了自由振动振型的多样性，这些自由振动将在动力传动装置各元件摩擦力矩的作用下迅速衰减。

强迫振动是在外部力矩作用下产生的振动。这些振动的频率等于产生振动的周期性干扰力的频率，也就是说与振源的振动频率成正比。当强迫振动的频率与传动系统的某一固有频率一致时，产生共振。这时，振动幅度最大，相应的频率称为共振频率。在动力传动装置中强迫振动的激励源可能是能源产生的不均衡转动力矩（发动机）以及这些能源的使用者（压缩机、泵等），路面不平度产生的车体振动，传递功率的装置产生的振动（履带板互相碰撞、齿轮啮合、一些回转零件的偏心）等。

路面或地形的不平度以及运动阻力矩的变化是发动机负载与转速大幅度变化的主要因素。转速的变化范围不由发动机轴的最大转速和最低稳定转速决定。在非稳态工况下，如不适时地由低速挡挂入高速挡时，会降低发动机轴的转速而使它低于最低稳定转速；当从高速挡挂入低速挡时，会使转速增加而超出最大允许值。

发动机工作具有较大转速变化范围，动力传动装置中自由振动和强迫振动振源的形式多种多样，很有可能发生共振。共振状态的主要特征是当负载数值很大时，动力传动装置的传动零件强度和使用寿命受到影响，并且位于共振区范围内共振频率上的发动机会空转。这种现象可能发生在克服阻力所需系统功率超出发动机供给功率（发动机起动时期）的情况下，此时发动机不能可靠起动。在动力传动装置工作时，频繁改变工况（转弯，加速，减速，坦克火炮发射炮弹）的过渡状态是十分重要的，这时动力传动装置各部件上作用着由惯性和振动两部分组成的脉冲负荷，且大多数情况下这些脉冲负荷将成为负荷的主要成分。由摩擦元件分离过程中车辆的速度和加速度、车辆行驶路线以及动力传动装置的一些部件转速随时间的变化，可以判断过渡状态。

过渡状态大都是非稳态过程。稳定性是指当向系统施加一些外作用力后，系统可以恢复到初始状态的能力。过渡状态的不稳定性（摩擦离合器摩滑时）是由于系统中产生了发散振动或自激振动。

运用模型分析动态过程就是指将所研究的物理现象分解，并建立一些数学简图。这些数学简图用来描绘一些外部作用和系统内零件、系统、受控对象、工作部件之间及车辆整体的相互作用。建立动态过程模型就是运用一些规则和假设，用理想模型替代实际动态过程。这些理想模型与原过程则依据最初参数准则等效。对研究对象的模拟还要求将弹性、耗散、惯性要素特性理想化，与外部环境的作用力和运动联系也要模型化。

2.实际系统的简化原则

车辆动力传动系统是一个非常复杂的连续弹性质量系统，对其进行动态性能分析时需要进行简化。进行简化时，理想地认为车辆动力传动系统是由一些只有转动惯量而无弹性变形的刚体和一些只有弹性变形而无转动惯量的弹性轴段组成。在简化过程中，遵循以下5点原则：

（1）忽略系统间隙，将动力传动系统转化为线性多自由度集中质量－弹性质量系统；

（2）转动惯量大且集中的部件为非弹性体，转动惯量小且分散的部件为无惯量弹性体；

（3）对于大惯量的部件，以其回转平面中心线作为该部件的质量集中点；

（4）相邻两集中质量间的连接轴，其转动惯量可平均地分配到两集中质量上，其扭转刚度就是两集中质量间的当量扭转刚度；

（5）激励力矩作用在惯性元件上。

3.典型部件转动惯量的确定

1）轴、齿轮等转动惯量的确定

材料力学提供了简单几何体零件转动惯量的计算公式，可以将齿轮和轴等零部件划分为若干简单几何体零件，分别计算其转动惯量，再进行合成，得到齿轮和轴的转动惯量。对于曲柄等复合回转体的转动惯量，可采用近似求解。

利用实验方法或Pro／e、UG、I－DEAS等软件可以精确地确定复杂形状零部件的转动惯量。

2）变转动惯量问题

最常见的变转动惯量问题是转动惯量随轴的旋转而周期性变化，如活塞连杆机构，它属于非线性问题，比较复杂，通常采用一些简化方法确定其转动惯量。

精确求解往复运动质量对轴系的回转惯量问题，要用能量方程式。例如，经分析计算，以曲轴回转一周能量守恒建立方程计算得，活塞组加连杆小端的往复运动质量的当量转动惯量Je为

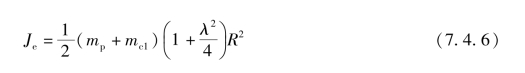
式中　mp——活塞组质量；

mc1——连杆小端往复运动质量；

λ——曲柄与连杆的长度比；

R——活塞半径。

3）平面行星齿轮系各部件的惯量

下面以单轴输入、单轴输出的单排平面行星齿轮系为例讨论行星架、太阳轮和齿圈转动惯量的计算方法。

（1）太阳轮为输入元件，行星架为输出元件。

太阳轮为输入元件，行星架为输出元件时，行星齿轮系几何运动及行星轮受力分析如图7.4.3所示。c、s、p和r分别代表行星架、太阳轮、行星轮和齿圈。假定太阳轮和齿圈的绝对位移φs和φr方向相同，设φs＞φr，于是得到s、p和r之间的相对位移关系。图7.4.3（b）中箭头方向表示功率流方向，取行星轮p为自由体，其受力分析如图7.4.3（c）所示。图中，Fc、Fs和Fr分别为行星架、太阳轮和齿圈作用在行星轮上的力。依据力矩、速度和几何关系得

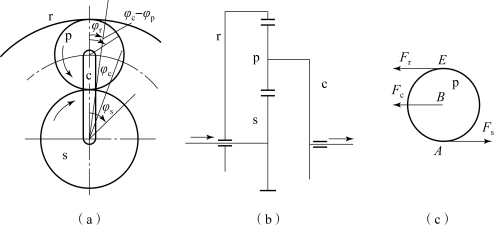
图7.4.3　行星轮系几何运动及行星轮受力分析图

（a）几何运动图；（b）行星排示意图；（c）行星轮受力分析

齿圈r制动时，太阳轮s对其旋转轴线的等效转动惯量为

齿圈r制动时，行星架c对其旋转轴线的等效转动惯量为

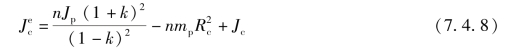
式中　Js——太阳轮对其旋转轴线的转动惯量；

Jc——行星架对其旋转轴线的转动惯量；

Jp——行星轮对其旋转轴线的转动惯量；

k——行星排参数；

n——行星排行星轮数目；

mp——行星齿轮质量。

（2）齿圈为输入元件，行星架为输出元件。

同样方法可求得太阳轮s制动时，齿圈r对其旋转轴线的等效转动惯量为

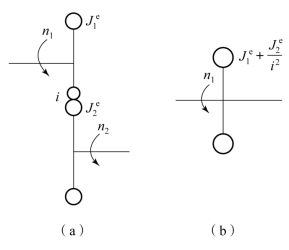
图7.4.4　平面行星轮系当量系统

（a）当量系统1；（b）当量系统2

（3）平面行星轮系的当量系统模型。

不考虑齿轮啮合刚度，输入输出元件之间有一定的传动比关系，可将行星排简化成定轴齿轮传动系统，建立2自由度（2个集中质量）当量系统模型，如图7.4.4（a）所示。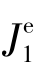和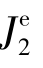是输入和输出元件对其旋转轴线的等效转动惯量；i为输入、输出元件的传动比。图7.4.4（a）进一步简化可得到平面行星轮系单自由度当量系统模型，如图7.4.4（b）所示。

4.典型部件扭转刚度的确定

用计算或试验方法可确定部件的扭转刚度，下面讨论用计算法确定部件的扭转刚度。

1）轴的扭转刚度

在材料力学中，轴的扭转刚度K定义为，在轴的全长范围内产生单位扭转角所需的扭矩。据此，依据材料力学公式可知，对于等直径圆轴有

式中　G——材料的剪切弹性模量；

D——轴的直径；

L——轴的长度。

对于传动系的复杂轴段，常简化为阶梯轴或者套轴，按照刚度串联或者并联的方法求解。轴端串联使轴变长，刚度减小。

在实际工程中，常遇到开有花键或者键槽的阶梯轴。目前，通常采用以下4种方法计算这类轴的扭转刚度。

（1）将开有花键或键槽的阶梯轴简化成与其最小横截面直径相等的圆轴，然后按材料力学的有关公式计算。

（2）用有限元法求解圣维南扭转应力函数。

利用图表和曲线查得各自的扭矩系数K后，分别求出花键轴段、键槽轴段和阶梯轴段各自的扭转刚度。然后，将计算所得结果按一定的法则，通过串联和并联的组合，最终求得全轴的扭转刚度。

（3）利用ANSYS、I－DEAS、ADAMS等软件进行计算，通过给零件施加约束和扭转力矩，得出所加力产生的角变形来计算轴段扭转刚度。

（4）利用经验公式，考虑花键连接和单键连接处的扭转刚度为

式中　β——花键连接和单键连接的系数，对于半圆键连接，β＝115 N／（rad·m3）；对于花键连接，β＝379 N／（rad·m3）。

d——连接处直径（花键连接时d＝dcp，dcp为花键节圆直径）（m）。

l——连接长度（m）。

h——键的有效长度（m）。

z——单键（花键）数。

2）万向节的扭转刚度

万向节的扭转刚度计算公式为

式中　A——系数，A＝32 N／（rad·m2）；

d——被连接轴的直径（m）。

3）盖斯林格联轴器的扭转刚度

盖斯林格联轴器是通过内部簧片的高弹性和油流动所形成的阻尼来改善轴系扭振的，它的扭转刚度是振动频率的函数，其经验公式为

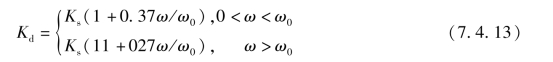
式中　Kd——联轴器动扭转刚度；

Ks——联轴器静扭转刚度；

ω0——联轴器自振频率；

ω——系统振动频率。

5.典型部件阻尼系数的确定

一般情况下，车辆动力传动系统中的能量消耗由零件材料中的滞后损失、键连接、轴承支承、齿轮啮合中的流动阻尼以及各种阻尼装置中的阻尼引起。零件材料中的能量损失可以不考虑，因为金属中的相对能量耗散比（一个振动循环内的能量散耗同整个循环的能量的比值）是很小的，一般为0.01～0.02。

车辆动力传动系统中的阻尼主要有发动机阻尼、轴段阻尼、联轴器阻尼、液力变矩器阻尼、减振器阻尼、惯量阻尼等，这些阻尼属于摩擦阻尼。摩擦阻尼具体可分为外阻尼和内阻尼。所谓外阻尼，就是系统各零部件表面和外界物体表面或介质摩擦产生的阻尼，如活塞与气缸之间、轴颈与轴承之间、变矩器叶片与液体之间的阻尼等；内阻尼是振动物体因变形而产生的分子之间的摩擦阻尼，也叫材料的滞后阻尼。车辆动力传动系统除了一般概念上的摩擦阻尼外，还包括一种“假阻尼”。由于轴系在扭振过程中转动惯量和扭转刚度的不稳定，使轴系的自振频率不稳定；又由于曲轴回转的不均匀度，使激励力矩的频率不稳定。所有这些不稳定因素都将使轴系的共振工况不易建立，使实际的共振振幅有所减小，将这种实际共振振幅的减小视为假阻尼的作用。

1）发动机阻尼系数

在进行车辆动力传动系统扭转振动计算中，估算发动机阻尼系数是必不可少的。计算阻尼的经验公式中，用放大系数和阻尼功的形式表示的阻尼系数公式比较多，但直接给出单气缸阻尼系数的公式尚少。单气缸阻尼系数一般是通过大量实验得到的，与发动机类型、单气缸结构、冲程长短、振型及频率等种种因素有关，还没有一个通用的阻尼系数计算公式解决所有问题。常用的与单气缸尺寸有关的单气缸阻尼系数公式为

式中　A——活塞面积（m2）；

R——曲柄半径（m）；(www.xing528.com)

ke——取决于机型的系数（N·s／m3）。

Wydler公式和Ker.Wilson公式具有这一形式，在Wydler公式中，重型机ke的取值为（0.04～0.07）×10－8；在Ker.Wilson公式中，高速机ke的取值为（1.407 2～4.221 6）×10－8。

2）液力变矩器阻尼系数

液力变矩器的减振性能被人们广泛认知，但其减振效果的定量分析一直是车辆动力传动系统扭振分析中的难题。

利用阻尼转矩及阻尼功的概念可得到确定液力变矩器阻尼系数的方法。假设液力变矩器的阻尼为线性阻尼，液力变矩器损失功率等于液力变矩器阻尼力矩所做的功，则液力变矩器阻尼力矩可表示为

式中　C——液力变矩器黏性阻尼系数；

φ·—扭振角速度。

车辆动力传动系统的激励按傅里叶级数展开为一系列不同谐次的正弦项的叠加，设在第r谐次简谐激励下，液力变矩器扭振角位移响应为

φr＝Ar sinωr t＋Br cosωr t

式中　Ar、Br——第r次激励下响应的正弦项和余弦项的扭振幅值；

ωr——第r次外激励角频率。

依据上述方法计算可得出C的计算公式为

式中　MP、MT——泵轮输入转矩、涡轮输出转矩；

ωP——泵轮角速度；

iy——液力变矩器的传动比，iy＝ωT／ωP，ωT为涡轮角速度。

依据式（7.4.16）可计算得到C是ωP的函数，可由试验数据拟合得到。

3）弹性联轴器阻尼系数

弹性联轴器阻尼以轴段阻尼形式考虑，联轴器的阻尼系数公式为

式中　K——联轴器扭转刚度；

ψ——损失系数；

ω——系统振动圆频率。

不同联轴器损失系数的取值如下：①橡胶高弹联轴器，ψ＝0.75；②塞销式联轴器，ψ＝0.085～0.1；③盖斯林格联轴器，当ω≤ω0时，ψ＝2π（0.2＋0.5ω／ω0）；当ω＞ω0时，ψ＝2π×0.7，ω0为联轴器的自振频率。

4）扭转减振器阻尼系数

（1）对于橡胶硅油减振器、盖斯林格减振器等有阻尼弹性减振器，阻尼以轴段阻尼形式考虑，阻尼系数为

式中　Kd——动扭转刚度；

ψ——损失系数，选取参见联轴器部分；

ω——振动圆频率。

（2）对于阻尼型减振器（如纯硅油减振器），阻尼以质量阻尼形式考虑，阻尼系数为

式中　Jd——纯硅油减振器惯性轮转动惯量。

（3）对于橡胶减振器，阻尼系数取为

式中　ξ——相对阻尼系数。

5）轴段阻尼系数

以轴段阻尼形式考虑，并作线性化处理，轴段的阻尼系数为式中　K——轴段扭转刚度。

6.当量系统模型

进行履带车辆动力传动部件动态特性计算，必须建立包括发动机、传动装置、整车在内的动力传动系统当量系统的力学模型，包括归一化及非归一化当量系统模型，以及刚性体和弹性体动力学模型。

1）归一化和非归一化当量系统模型

（1）建模假设。

对履带车辆动力传动系统，由于动力传递路线随动力传动系统挡位的不同而不同，因此动力传动系统模型随挡位的不同也有所变化。建立力学模型时，遵循能量守恒原则，即转化前后系统的势能、动能和耗散能保持不变。

（2）归一化当量系统模型。

目前，车辆动力传动系统动力学研究计算模型普遍采用归一化当量系统模型。根据转换前后系统的动能、势能和耗散能保持不变的原则，各旋转件的转动惯量、扭转刚度及阻尼系数等原始参数按式（7.4.22）转换到系统某一轴上。转换后的模型称为归一化当量系统模型。归一化当量系统模型的建立分两步：一是将原系统简化，求得集中质量－弹性轴系统的转动惯量、扭转刚度等参数；二是进行归一化处理。

归一化的表达式为

式中　C′、K′、J′、n′、M′——转换前系统（即原系统）某部件的阻尼、扭转刚度和对其旋转轴线的转动惯量、转速和扭矩；

C，K，J，n，M——转换后系统（即当量系统）某部件的阻尼、扭转刚度和对其旋转轴线的转动惯量、转速和扭矩；

i——当量系统归一化的轴到原系统实际轴的传动比。

（3）非归一化当量系统模型。

非归一化当量系统模型为面向部件建模。建模时，转动惯量、扭转刚度及阻尼系数等原始参数不向某一轴进行转换，系统原始参数不变，这种模型称为非归一化当量模型。非归一化当量系统模型的特点如下：

①模型的参数物理意义明确，模型清晰易读、建模过程简单；

②仿真过程中不用进行各挡间不同转动惯量的切换，仿真过程更快捷；

③在后续的仿真计算中，可得到系统中任一部件的运动学和动力学响应；

④部件通用性好，利于模块化建模。

非归一化当量系统模型如图7.4.5所示。图中，CT代表液力变矩器闭锁离合器；CL、CH、CR、C1、C2和C3分别代表动力换挡离合器；P、T和D分别表示液力变矩器泵轮、涡轮和导轮；分别表示发动机、液力变矩器泵轮和涡轮转动惯量；表示换挡离合器主动部分或者被动部分的转动惯量；J′V为整车质量等效转动惯量；i1、i2、i3、i4为传动比。

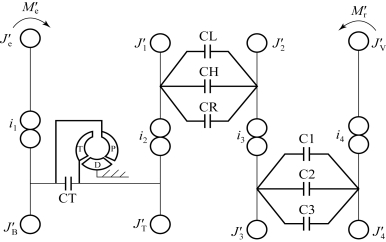
图7.4.5　非归一化当量系统模型

2）刚性体和弹性体当量模型

（1）车辆传动刚性体当量模型。

简化分析常采用刚性体动力学模型进行车辆传动系统动态特性计算。忽略系统的弹性和阻尼，将各构件视为由单一的惯性环节所组成，得到包含发动机、综合传动和整车质量的动力传动系统的刚性体动力学当量模型。

车辆综合传动系统刚性体动力学当量模型的一般形式如图7.4.6所示，该模型为归一化当量模型。发动机和曲轴系统简化为一个集中质量，发动机的转矩作用其上。液力变矩器泵轮、涡轮分别以集中质量来表示，车辆传动系统简化为8自由度模型。

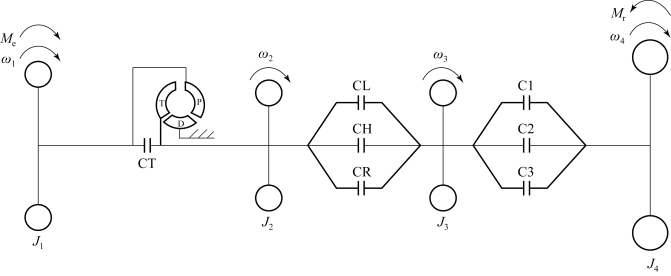
图7.4.6　车辆综合传动系统刚性体动力学当量模型的一般形式

图7.4.6中，J1表示发动机至液力变矩器泵轮的当量转动惯量，J4为整车质量当量转动惯量，J2、J3表示换挡离合器主动部分、被动部分的当量转动惯量，ω1、ω2、ω3、ω4表示对应部分的角速度，Me和Mr分别表示发动机激励力矩和作用在整车上的阻力矩。

（2）车辆传动弹性体当量模型。

将车辆传动系统简化成线性多自由度集中质量－弹性－阻尼系统，即系统由无惯性的弹性环节和无弹性的惯性环节组成，同时考虑阻尼作用。实际系统各部件以集中质量存在。在简化过程中，忽略轴的横向振动，忽略轴承和轴承座的弹性。阻尼有发动机阻尼、液力变矩器阻尼、轴段阻尼和集中质量阻尼等。车辆综合传动系统弹性体动力学当量模型的一般形式如图7.4.7所示。该模型为归一化当量模型，车辆传动系统简化为8个自由度的弹性体动力学模型，忽略集中质量阻尼的作用。

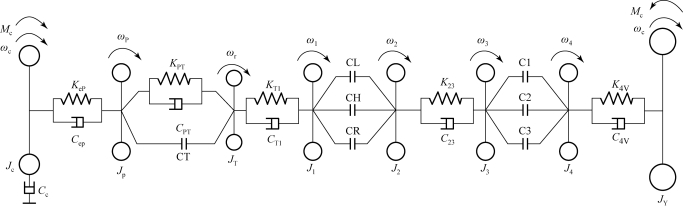
图7.4.7　车辆综合传动系统弹性体动力学当量模型的一般形式

图7.4.7中，Kep、KT1、K23和K4V表示两个集中质量间轴段的当量扭转刚度，Cep、CT1、C23和C4V表示两个集中质量间轴段的阻尼，KPT表示液力变矩器的等效扭转刚度，CPT表示液力变矩器的阻尼，其余参数意义同图7.4.6。机械工况时，液力变矩器闭锁离合器CT闭锁，液力变矩器等效扭转刚度和阻尼不起作用；液力工况时，CT解锁，液力变矩器正常工作。

3）当量系统的简化方法

车辆传动系统自由度多，模型结构复杂，可根据研究的目的和精度要求，按照一定原则进行简化。目前有许多简化系统的方法，用得最多的是偏频方法。这种方法的基础是用双质量系统代替单质量系统或者用单质量系统代替双质量系统，简化的原则如下。

（1）简化系统的偏频等于被替换的原系统的偏频。

（2）要求ω≫ωlim。这里ω为原系统频率，ωlim为所研究的动态系统频率范围上限。ω的计算公式为

式中，对于单质量系统，J＝Jm，K＝Km＋Km－1；对于多质量系统，J＝Jm Jm＋1／（Jm＋Jm＋1），K＝Km。

（3）在考虑的频率范围内，简化系统的固有频率和振型与被替换的原系统的特性一致，一般情况下，如果研究中只考虑系统前n阶的固有频率和振型，则最后简化系统的自由度数应不少于n＋2个。

双质量系统代替单质量系统如图7.4.8所示。双质量系统代替单质量系统时，双质量系统的参数为

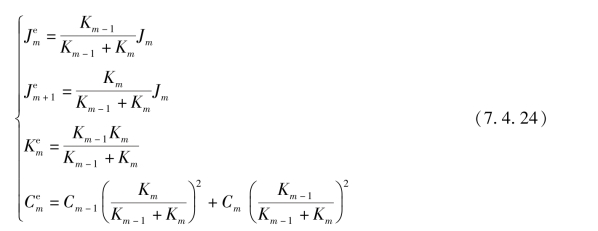
单质量系统代替双质量系统如图7.4.9所示。

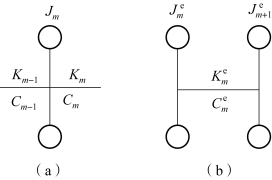
图7.4.8　双质量系统代替单质量系统

（a）单质量系统；（b）双质量系统

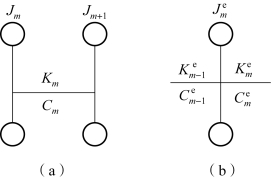
图7.4.9　单质量系统代替双质量系统

（a）双质量系统；（b）单质量系统

单质量系统代替双质量系统时，单质量系统的参数为

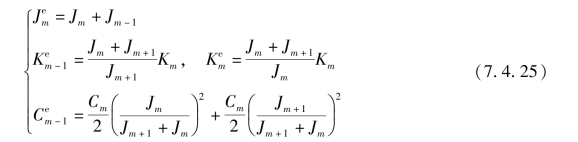
把得到的等效系统代入总的动态系统来代替原来的局部系统，这时得到的系统相应的参数应与未进行变换的系统的相应参数合并。如果原系统是边界系统，那么简化方法仍一样，仍保留自由扭转刚度部分，这部分不影响系统的动态过程，可以忽略不计。