车辆转向中横向和纵向力复合作用的仿真实践

图6.3.19　坦克在斜坡上转向时的受力分析

1.斜坡转向

前面讨论的坦克上坡转向、下坡转向、侧倾坡向上和向下转向都是坦克处于特殊情况下的转向，即坦克重力的坡道分力都是单纯的横向力或纵向力的情况。坦克在斜坡上，即坦克在同时具有纵向倾角又具有横向倾角的坡道上的转向称为斜坡转向。这种情况下，坦克将同时受到横向力和纵向力的作用。

设坡角为α，则坦克平行于坡面指向坡下方向的重力分力为G sinα。假设该分力与通过车辆中心的纵向对称轴线间的夹角为φ，则可将重力分力G sinα分解为一个纵向力Fx＝G sinαcosφ和一个横向力Fy＝G sinαsinφ，如图6.3.19所示。

纵向力Fx对坦克转向的影响与坦克上、下坡转向相似，横向力Fy对坦克转向的影响与坦克在侧倾坡上转向相似。在前面分析内容的基础上，可用类似的方法求出斜坡转向的两侧履带上转向所需的牵引力和制动力。

通过对坦克在纵向坡道和侧倾坡道上转向动力学分析的结论可以知道，纵向力对履带接地段法向负荷分布图形和坦克转向阻力矩的影响相对较小，特别是在常见坡角范围（α＜15°），式（6.3.7）中转向阻力矩修正系数K≈1。此时，纵向力作用下的转向阻力矩表达式与水平地面相似，只需将车重G替换为附着重力Gf＝G cosα即可。纵向力主要直接影响纯上坡和纯下坡转向所需的牵引力和制动力大小。所以，为了简便计算，在分析坦克斜坡转向动力学问题时，可以不考虑纵向分力对履带接地段法向负荷分布的影响，只考虑横向分力引起的法向负荷变化，仅将纵向力看作一个作用在坦克平面上的单纯外力。

斜坡上坦克受到的横向分力Fy＝G sinαsinφ所引起的转向极偏移量可以采用同式（6.3.19）类似的推导方法进行分析，不难得出斜坡转向情况下只考虑横向分力影响的转向极偏移量为

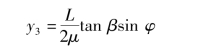
按照与侧倾坡转向工况相类似的推导过程可以得到斜坡转向时的转向阻力矩Tμ，它与式（6.3.20）完全相同，即

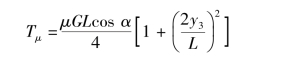
坦克在斜坡上转向时，两侧履带受到的地面（直线）行驶阻力为

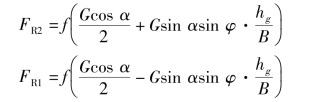
在图6.3.19中分别列两个坦克平面的力矩平衡关系，就可求得转向所需牵引力F2和制动力F1。

所有外力和外力矩对O1点取矩，列出对O1点的力矩平衡式，得

故有

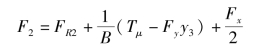
所有外力和外力矩对O2点取矩，列出对O2点的力矩平衡式，得

故有

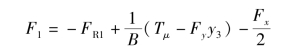
当坦克在一定坡角的斜坡上做360°整周转向运动时，纵向力Fx和横向力Fy均随转角φ的变化而变化，因而F2和F1也随之相应变化。E.U.伊凡诺夫曾经对斯大林Ⅲ号重型坦克，在α＝5.5°的斜坡上做过转向试验，找出了φ由0°到360°，以固定半径进行转向时，F2、F1随φ变化的情况，如图6.3.20所示，虚线为用仪器测得的变化曲线，实线为按公式计算所得的理论曲线。

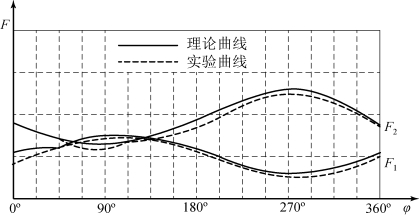
图6.3.20　车辆在坡上做360°整周转向时的F2、F1

由图6.3.20可以看出，试验测得曲线与理论计算曲线很吻合，其变化规律是一致的。说明采用上述简化计算方法是足够精确的，可以满足工程应用的需要。

如果使坦克在一定坡角的坡道上以一定半径进行360°转向，F2、F1的变化规律如图6.3.21所示。纯上坡转向时，F2最大而F1最小；纯下坡转向时，F2最小而F1最大；侧倾坡向上转向时，F2和F1均较大；侧倾坡向下转向时，F2和F1均较小；斜坡转向时，F2和F1介于纯上（下）坡转向和侧倾坡转向之间。由此可知，纯上坡转向是最困难的转向工况。在相同的转向条件下，需要高速履带提供的牵引力F2最大。因此，在转向机构设计或对转向机构进行验算时，应以纯上坡转向作为计算条件。而纯下坡转向时，所需制动力F1最大，因此转向机构中的制动元件设计与校核，应以纯下坡转向为计算条件。

2.高速转向

前面讨论了由地面坡角所引起的横向力或纵向力对坦克匀速转向运动的影响规律，实际上坦克除了在坡道上转向外，在其他一些条件下（即使在水平地面上转向时）也会受到横向力或纵向力的作用。下面以坦克在水平地面上高速转向为例来进行分析。

前面的内容都是假设坦克的转向运动是在低速条件下完成的，没有考虑转向运动时坦克离心力的影响。但在高速转向时，离心力的作用就不可忽视了。因此，在讨论高速转向时，主要讨论离心力对坦克转向的影响。

坦克在水平地面上高速、匀速转向时的受力分析如图6.3.22所示。与低速转向相比，此时在坦克的重心（假设重心在坦克平面中心C点上）上会有一个较大的离心力FL。离心力FL作用在坦克平面中心C点和转向中心O点的连线上，其方向始终指向高速侧（外侧）履带。

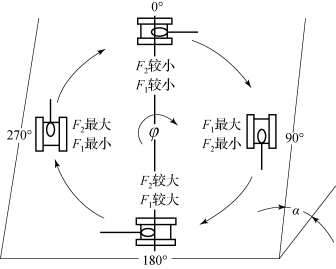
图6.3.21　车辆在做360°转向时各位置F2、F1的比较

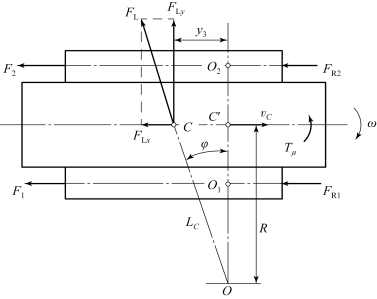
图6.3.22　高速转向时坦克所受外力

离心力FL的大小与坦克质量m、C点和O点之间的距离LC（就是重心做圆周运动的轨迹半径）以及旋转角速度ω有关，即(www.xing528.com)

FL＝mω2 LC

式中　m——坦克全质量（kg）；

ω——坦克旋转角速度（rad／s）；

LC——坦克平面中心C点到转向中心O点之间的距离（m），LC＝R／cosφ。

离心力FL可以分解为一个纵向分力FLx和一个横向分力FLy，假设OC连线与OC′连线的夹角为φ，则FLx和LLy的大小为

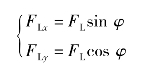
在正常情况下，坦克高速转向时的转向半径R一般都比较大，OC连线与OC′连线的夹角φ则较小，所以离心力的横向分力远大于纵向分力，即FLy≫FLx。所以，高速转向时履带接地段法向负荷分布图形主要受横向分力的影响。与上节中的分析类似，这里只考虑横向分力FLy对接地段法向负荷分布、横向阻力分布和转向阻力矩的影响。

由于离心力横向分力的方向永远指向高速侧履带，这与坦克在侧倾坡上向坡上转向的情况类似，因此此时坦克履带接地段的转向极必然会产生向车首方向的偏移。转向极偏移量仍用y3表示，其大小可以用与式（6.3.19）相同方法表示，在水平地面上Gf＝G，即

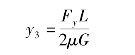
式中　μ——单位横向阻力和单位法向负荷之间的比例系数，也是转向阻力系数。

高速转向时，外侧履带重载，单位法向负荷q2较大；内侧履带轻载，单位法向负荷q1较小，即q2＞q1，因此法向负荷分布和横向阻力分布仍为矩形。

两侧履带单位法向负荷q1和q2为

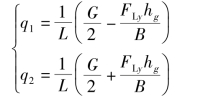
高速转向时履带接地段横向阻力分布如图6.3.23所示。

按照与侧倾坡向坡下转向工况相类似的推导过程可以得到水平地面高速转向时的转向阻力矩Tμ，它与式（6.3.20）形式相同，即

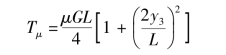
根据图6.3.22分别列出纵向力平衡方程式和力矩平衡方程式，就可求出转向所需牵引力F2和制动力F1。平衡方程式为

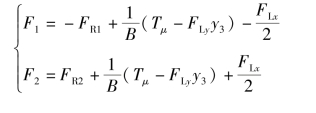
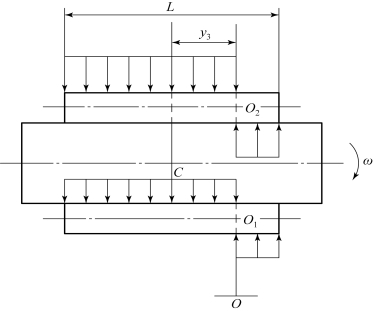
图6.3.23　高速转向时横向阻力分布

即

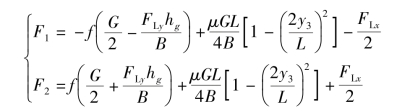
由上式可知，F1随μ、G、L的增加而增加，随FR1、B、FLx的增加而减小；F2随FR2、G、μ、L、FLx的增加而增加，随B的增加而减小。

对于给定的坦克在给定的地面上，以一定的半径高速转向时，对F1、F2的主要影响因素是转向角速度ω。随着ω的增大，离心力FL增大，FL增大使FLx、FLy都增大。其中，FLy是主要影响因素，FLy增大的同时也使得y3增大，从而使F1、F2显著减小。

总之，随FL的增加使F1、F2都减小，所以离心力对转向是个有利因素。但应注意，转向速度不应太高，太高会引起坦克侧滑而失去控制，极易发生事故。

当坦克以很高的角速度在平滑坚硬的地面上做匀速转向时，离心力很大，其横向分力可能达到甚至超过坦克的横向附着力，这时坦克便产生侧滑。当离心力横向分力等于横向附着力μG时，转向极偏移到履带接地段的端点，偏移量达到最大值y3max＝L／2。这时，坦克处于匀速转向和侧滑的临界状态，这时的车速称为高速转向的极限速度vClim，也就是转向允许的最大车速。相应的转向半径称为极限半径Rlim，即在该车速下转向时所允许的最小转向半径。

在发生侧滑的临界状态下有

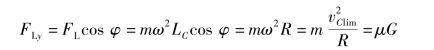
由上式可得此时的极限车速为

或

式中　g——重力加速度，g＝9.8 m／s2。

由式（6.3.24）可知，高速转向发生侧滑的极限车速vClim与地面的转向阻力系数μ（这里也可以理解为地面的横向附着系数）和转向半径R的大小有关。地面性质不同，侧滑的极限速度也不同，如图6.3.24所示。如果地面的转向阻力系数或横向附着系数比较大（如草地等），一般来说坦克不容易发生侧滑，但高速转向过程中可能会出现侧翻的危险情况。所以，在高速转向过程中一定要控制好车速，尽量避免侧滑和侧翻的出现。

图6.3.24　极限速度和极限半径以及转向阻力系数的关系

总结高速转向时离心力对转向的影响，可得如下结论：在保证坦克不产生侧滑的前提下，转向速度越高越好，离心力越大越好，这有助于提高转向灵活性。