纵向力下的转向：车辆系统仿真理论与实践

1.上坡转向

坦克在纯纵向坡道上坡转向时，过坦克重心垂直于地面的纵向平面内，坦克的重力G可以分解为两个分力（见图6.3.1）：一个为垂直于地面的法向分力（即附着重力）Gf＝G cosα；另一个为平行于地面的纵向分力Fx＝Fp＝G sinα（这里纵向力就是坡道阻力），Fx就是作用在坦克重心上的纵向力。坦克重心高度以hg表示，道路坡角以α表示。下面研究在纵向力Fx作用下，坦克的匀速转向和水平地面上有什么不同。

1）压力中心纵向偏移量

坦克在水平地面上转向时，地面法向反力FN的压力中心正好和坦克平面中心C相重合。但是在纵向力Fx作用下情况发生了变化，地面法向反力的压力中心不再和C点重合，而是向车体尾部纵向偏移，偏移的距离称为压力中心偏移量x0，如图6.3.1所示，且

2）法向负荷分布

压力中心纵向偏移量实际上反映了履带接地段法向负荷分布图形的变化，由于在上坡时纵向力Fx的方向是指向车体尾部，因此接地段后部的单位法向负荷q增加，前部减小。可以合理地假设接地段法向负荷分布图形由矩形变为梯形，如图6.3.2所示，并且近似认为两侧履带接地段的法向负荷梯形是完全一样的。为了研究方便，假设把两侧履带接地段上的法向负荷都集中在一个假想的接地段上，这个接地段既不在内侧也不在外侧，而是在坦克平面的纵向轴线上，两条履带接地段上的总法向负荷梯形图为ABFE，如图6.3.3所示。

为了求出履带接地长度上各点单位法向负荷的大小，先求出接地段的前端、后端及中部单位法向负荷q1、q2及q0的大小。

根据单位法向负荷的定义和图6.3.3中的几何关系，接地段中部单位法向负荷，即平均单位法向负荷q0可由下式表示：

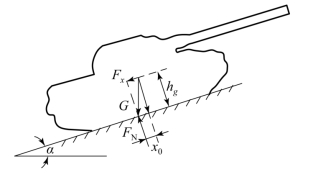
图6.3.1　重力分解和压力中心偏移

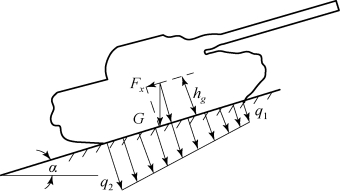
图6.3.2　上坡转向时接地段法向负荷分布

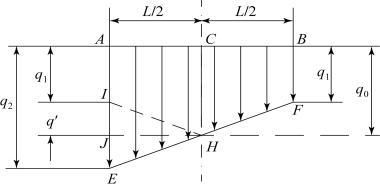
图6.3.3　履带接地段的总法向负荷分布图

过H点作一虚线HJ，由图6.3.3可知，q1、q2、q0及q′有如下关系：

式中　q′——图6.3.3中线段IJ和JE的长度。

地面法向反力FN对C点之矩FN x0等于梯形图ABFE对C点之矩，也等于等腰三角形HIE对C点之矩，即

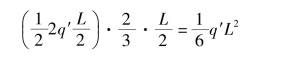
则有　

可得

将式（6.3.3）代入式（6.3.2）可得

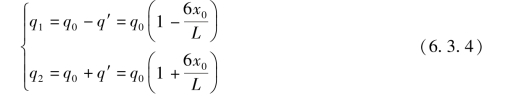
由此可知，已知G、α、hg、L及x0，就可由该式求出q1、q2。当q1、q2求得后，就可作出法向负荷梯形图ABFE。

3）转向极的纵向偏移量

由于纵向力Fx的作用，两侧履带接地段转向极（瞬时转向中心）O1和O2不能再保持在履带接地段中心C1和C2上。在上坡转向过程中，O1和O2必然会发生纵向偏移，转向极的纵向偏移量用y3表示，以区别于考虑滑转滑移条件下实际转向过程中的转向极的横向偏移量y1和y2。转向极的纵向偏移现象是转向阻力横向力平衡的要求，换句话说，如果转向极没有纵向偏移，那么转向过程中两侧履带上的横向阻力就无法平衡。这是因为横向阻力分布图形与法向负荷分布图形是成一定比例的，当法向负荷分布图形变为梯形时，横向阻力分布图形也变为梯形。要想使履带前半段和后半段的横向阻力平衡，转向极（也就是前半段和后半段横向阻力的转折点和分界点）必然会向单位法向负荷大的一段偏移一定距离，否则在匀速转向情况下横向力平衡这一必要条件就无法满足。上坡转向过程中转向极的偏移和两侧履带上横向阻力分布图如图6.3.4所示。

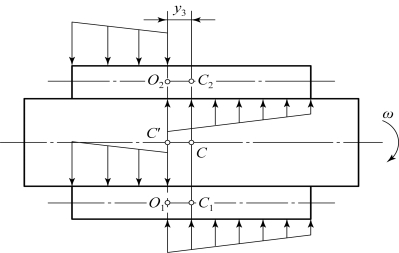
图6.3.4　上坡转向过程中转向极偏移和横向阻力分布图

为了求出上坡转向过程中的转向阻力矩，必须首先确定转向阻力的分布情况。要想确定转向阻力的分布图形就必须先求出转向极的纵向偏移量y3。下面将通过横向力平衡方程求取y3。

由于上坡转向过程中两侧履带上所受到的横向阻力分布情况一致，因此为了分析简便，仍把两侧接地段上的横向阻力集中在一个假想的履带接地段上，总的横向阻力分布如图6.3.5所示。

图6.3.5中，总横向阻力分布为MNPQ和TUVW两个梯形，要求出这两个梯形图面积的大小（即为横向阻力合力的大小），必须先求出该接地段前端、后端和转向极处（C′点的位置）的单位长度横向阻力μq1、μq2、μqy。在前面已经求得q1和q2，只有转向极处对应的单位法向负荷qy是未知的。qy可根据图6.3.6中相似三角形的几何关系求得，即

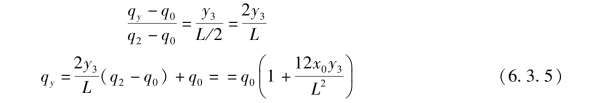
得到了qy与y3的表达式后，就可以由匀速转向时的横向力平衡关系，求出y3值。由于图6.3.5中横向阻力梯形图面积的大小就是其横向合力的大小，所以横向力平衡关系在这里就是指梯形MNPQ和TUVW的面积相等，即

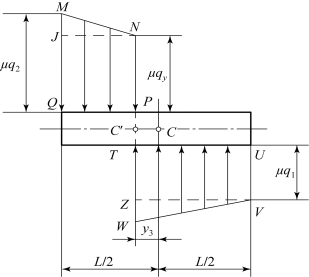
图6.3.5　上坡转向过程中两侧履带上总横向阻力分布图

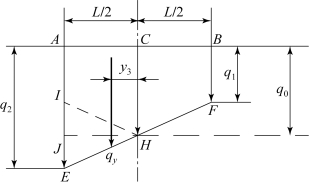
图6.3.6　转向极处对应的单位法向负荷qy

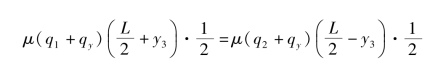
将式（6.3.5）和（6.3.4）代入上式得到一个关于y3的一元二次方程，即

解方程的根就可以得到转向极横向偏移量y3的大小，这里只取符号为“＋”的根，即

由式（6.3.6）可知，转向极横向偏移量y3和压力中心纵向偏移量x0及接地长L有关。

4）转向阻力矩

确定了转向极横向偏移量y3后，就确定了图6.3.5中所示的转向阻力分布。下一步将求解上坡转向过程中坦克受到的转向阻力矩Tμ。实际就是求图6.3.5中梯形MNPQ和TUVW的面积对C′点的合力矩。

为了方便计算，可在图6.3.5中作两条水平虚线JN和ZV，将两个梯形分解成一个三角形和一个矩形之和。每个图形（三角形或矩形）的面积就代表了一部分横向阻力合力的大小，各图形的重心就是这部分横向阻力合力的作用点。所以，各部分横向阻力对C′点之矩，就等于相应图形面积与该图形中心到C′点距离的乘积，即

△MJN对C′点之矩为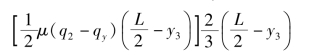　　

□JNPQ对C′点之矩为　　

△ZVW对C′点之矩为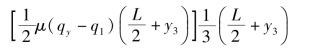　　

□TUVZ对C′点之矩为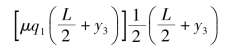　　

上述各图形对C′点的力矩之和即为坦克转向阻力矩Tμ，将式（6.3.5）和（6.3.4）代入整理后可得下式，即

式中　K——转向阻力矩修正系数，且

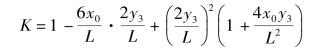
K值和x0、y3以及L有关，而x0、y3又和坡角α有关。随α的增加，x0和y3均增大，K值减小。反之，α减小使x0和y3减小，K值增加。α＝0时，x0＝0，y3＝0，K＝1。在上坡转向过程中，K、x0／L、y3／L和转向阻力矩Tμ随坡角α变化而变化的规律如表6.3.1和图6.3.7所示。(www.xing528.com)

表6.3.1　不同α值下K、x0／L、y3／L和Tμ的数值大小

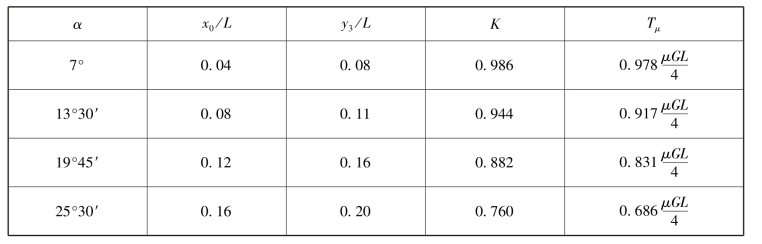
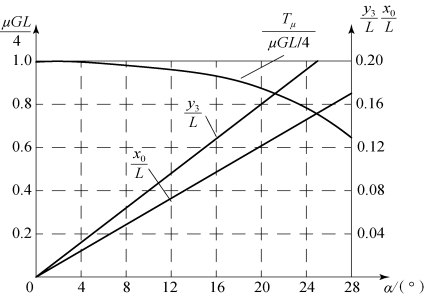
图6.3.7　x0／L、y3／L、Tμ和α的关系曲线

在常见坡角α＜15°时，K值接近于1。所以，在简化计算中，可假设K＝1，这时上坡转向的转向阻力矩表达式可以简化为

从图6.3.7可以看出，随着坡角α的增大，上坡转向的转向阻力矩Tμ逐渐减小，这说明在相同性质的地面上（f、μmax相同），做同样半径的转向（R和μ也相同），上坡转向比水平地面转向所受到的转向阻力矩小。但这并不能说明上坡转向就一定比水平地面转向容易。判断转向容易还是困难要根据转向时高速侧和低速侧履带上所需的牵引力F2和制动力F1进行判断。而转向所需的牵引力和制动力不仅与转向阻力矩有关，还与坦克平面受到的其他外力有关。上坡转向时，坦克平面上多了一个纵向力Fx＝G sinα，这个力也会直接影响F2和F1的大小。

5）转向所需牵引力和制动力

匀速上坡转向时坦克平面的受力分析如图6.3.8所示。已求得Tμ后，就可以利用纵向力平衡关系和力矩平衡关系建立两个方程，求出转向所需牵引力F2和制动力F1。

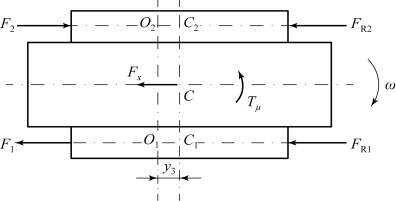
图6.3.8　匀速上坡转向时坦克平面受力分析

根据∑Fx＝0，可得F2－F1＝FR1＋FR2＋Fx；

根据∑MC＝0，可得。

联立求解上述两个方程式，可得坦克匀速上坡转向所需牵引力F2和制动力F1，即

将已知的FR1＝FR2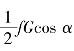＝、Fx＝G sinα和代入上式，得

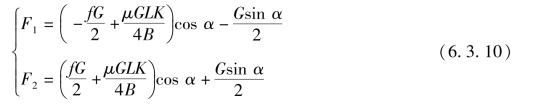
当α＜15°时，K≈1，上式可以简化为

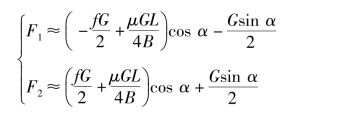
由式（6.3.10）可知，坦克匀速上坡转向所需牵引力F2和制动力F1随各种参数的变化规律比较复杂，难以直接看出坡角α对它们的影响，需要经过一定的计算分析后才能得出有关结论。图6.3.9为经过计算得到的一定条件坦克匀速上坡转向所需牵引力F2和制动力F1随坡角α的变化规律。

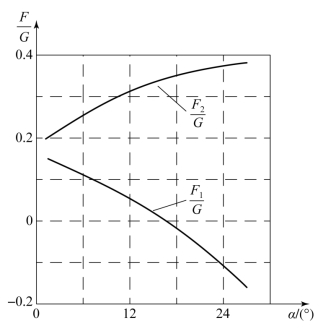
图6.3.9　牵引力F2和制动力F1随坡角α的变化规律

从图6.3.9可以看出，当给定车辆（G、L／B一定）在给定地面上（f、μmax一定），以一定的半径（μ一定）转向时，随α增加，F2增加。所以，上坡转向所需F2大于同条件下在水平地面上转向所需的F2，需要发动机提供更大的牵引力，即上坡转向比在水平地面转向困难。

同时，α增加使F1减小。当α增大到一定角度时，F1可以变为零，此时不需要低速侧履带提供制动力，所以上坡转向所需制动力小于同条件下的水平地面转向所需的制动力。这说明上坡转向时坦克转向机构摩擦元件（通常为制动器）的工作负担比水平地面上小，对低速侧制动器工作有利。当α过大时，低速侧履带的制动力将变为牵引力，此时如果操作不当会出现低速侧履带倒转的情况。

所以，在坦克上坡过程中应当提前对好方向，尽量避免转向，特别是半径较小的转向。在转向时还应当适当加大油门，以防止发动机熄火。在中等以上坡道上转向时，应使用短促、断续的小角度转向，不能长时间大角度转向，以防发动机熄火或高速侧履带打滑，或者低速侧履带倒转而造成事故。

2.下坡转向

坦克在纯纵向坡道上下坡转向时，重力分解和上坡转向时完全一样，所不同的仅是纵向力Fx＝G sinα的方向和上坡转向时相反。匀速下坡转向时坦克平面受力分析如图6.3.10所示。

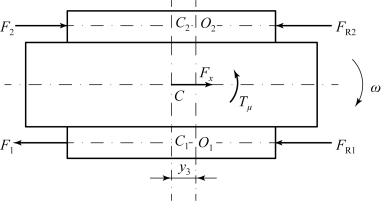
图6.3.10　匀速下坡转向时坦克平面受力分析

由于下坡转向时车辆、地面、坡道角度等都和上坡转向一样，因此下坡转向时的接地段法向负荷分布图形、压力中心偏移量和转向极偏移量产生的原因、计算方法与上坡转向时完全一样。但下坡转向时，纵向力Fx的方向是指向车体的首部，所以下坡转向的法向负荷图形为前大后小的梯形，压力中心和转向极都向车首偏移。

上坡转向分析过程中的式（6.3.1）～式（6.3.8）完全适用于下坡转向过程。下坡转向所需牵引力和制动力公式和上坡转向的式（6.3.9）和式（6.3.10）基本相同，只需将式（6.3.9）和（6.3.10）中纵向力Fx前的正负号颠倒过来即可，即

通过前面的分析可知，纵向力Fx对转向所需牵引力F2和制动力F1的影响是最大的，所以下坡转向时在Fx的作用下，随着α增加，F2将显著减小。当α增大到一定值时，F2甚至可以等于零，这说明当其他条件相同时，下坡转向比在水平地面转向容易。

同时，随着α增加，F1将增大，这说明下坡转向时坦克转向机构摩擦元件（通常为制动器）的工作负担比水平地面上大，对低速侧制动器工作不利，驾驶员操作制动器也比较费力。通常在设计转向机构时要将下坡转向作为转向机构强度校核的工况。

3.下坡反转向

装有独立式转向机构的坦克，在下坡转向中有时会出现反转向现象。所谓反转向就是拉一侧操纵杆，车辆却向另一侧转向的现象，叫反转向。

1）下坡反转向的条件

下坡反转向现象的出现需要两个必要条件：一个是发动机制动（或联合制动）；另一个是必须是独立式转向机构且使用分离转向工况，二者缺一不可。实现下坡反转向的充分条件是下坡角α＞arctan f，实际使用中坦克下坡时较容易具备这个条件，故常称之为“下坡反转向”。其实，在平地行驶的车辆，如果操作不当也会出现反转向。例如，车辆高速行驶中遇到险情突然减油再拉分离转向，就会形成反转向，在使用过程中应当尽量避免出现反转向现象。

2）下坡反转向的力学分析

车辆下陡坡都要采用发动机制动或联合制动，因此容易满足反转向的条件。现以发动机制动说明反转向形成的原因。

坦克在长而陡的坡道上（坡度角α＞7°）下坡直驶时，在坦克重心上作用着一个纵向力Fx＝G sinα。当Fx大于坦克地面行驶阻力FR＝fG cosα时，为了保持匀速运动，防止坦克加速下滑，常用发动机对坦克进行制动。此时，两侧履带上作用的制动力为FZe1和FZe2，如图6.3.11（a）所示。

在下坡匀速转向过程中，当切断内侧履带与发动机动力联系即分离内侧离合器（这是独立式转向机构的特点），而尚未对该侧制动器施加制动的瞬时（此时为分离转向工况），纵向力Fx与外履带发动机制动力FZe2形成一个力矩，该力矩的方向和驾驶员操纵的摩擦元件方向相反，它使坦克沿着与驾驶员操纵意图相反的方向转向，极易造成危险，如图6.3.11（b）所示。

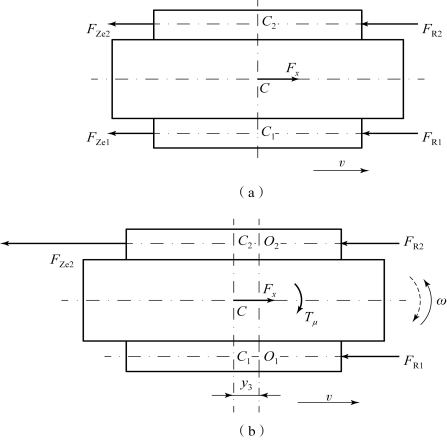
图6.3.11　下坡反转向受力分析

（a）发动机制动时下坡直驶受力分析；（b）下坡反转向过程受力分析

3）下坡反转向半径及其影响因素

下坡反转向是一种失控状态，其转向半径无法预知。如果车速较高而反转向半径较小，坦克就有出现侧滑甚至侧翻的危险。下面对下坡反转向的半径及其影响因素进行理论分析。

在图6.3.11（b）中，列出各种外力和外力矩对高速侧履带接地段中心C2点的力矩平衡关系式，即

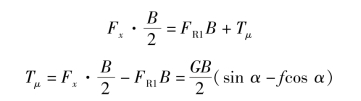
将下坡转向阻力矩近似表达式代入上式中，经整理可得

将转向阻力系数经验公式（注意其中包含转向半径）代入上式，可以求出下坡匀速反转向的理论转向半径Rfz，即

从式（6.3.13）可以看出，下坡反转向半径Rfz的大小与结构参数L、B，地面条件f、μmax和坡角α有关。在其他参数一定的条件下，Rfz随坡角α的增大而减小。这是因为坡角α越大，推动坦克下坡的纵向力Fx＝G sinα也越大，为保证匀速下坡，发动机制动力也越大，因此对高速侧履带的制动力也大，反转向力矩也大，转向半径就小。

一般而言，地面的f越大，μmax越小，反转向的半径就会越小。例如，取L＝3 m，B＝2 m，μmax＝0.3，f＝0.05，α＝15°时，利用式（6.3.13）计算出理论的下坡反转向半径Rfz＝1.28 m。当坦克在这样的坡道上发生反转向时，转向半径很小，在车速过高的情况下极易出现侧滑现象。

能实现反转向的下坡角α，必须大于运动阻力制动时的匀速下坡角。这是车辆能实现下坡反转向的充分条件，即下坡角α＞arctan f时，才有可能实现下坡反转向。因为车辆在这样的坡道上匀速下坡只靠运动阻力制动不能实现匀速行驶，只有利用发动机制动来实现，才有可能实现下坡反转向。

车辆平地行驶，如果处于发动机制动状态，再用分离转向也会形成反转向，这种情况容易造成事故，应当避免。因此，使用中采用分离转向时要平稳加油，否则不但转向不灵，甚至可能产生反转向。