汽车稳态转弯行驶是指方向盘转过一个固定的角度行驶或者绕着一个半径一定的圆周行驶。其实这种稳态不能算汽车动力学，而是属于静力学范畴。等半径的圆周在实际生活中极少见，只在高速公路交叉的地方才能找到。一般公路转弯的地方都是半径变化的弧线。但是因为汽车的转弯性能备受关注，所以测试和衡量的目标就转移到简单的模型和易于实行的实验上。
借助理论和实验论文能详尽地解释那些非专业人员也并不陌生的字眼，如不足转向、中性转向和过多转向。几乎每个汽车生产公司在自己的实验场地都备有一个“转盘”或“转向试验场”，用于进行操纵稳定性测试。其中，重要的因素一方面是所需的方向盘转角，另一方面是汽车的质心侧偏角，后者正越来越受到重视。
借助后轮主动参与转向（全轮或四轮转向）可以对质心侧偏角任意施加影响，甚至可以将它置于零，某些专业人士将这种状态视为驾驶员所期望的结果。在稳态圆周行驶时
在这些前提条件下，式（5.1.19）变为
（a11 a22－a12 a21）β＝（a12 b2－a22 b1）δV
则有
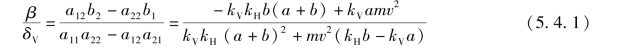
用5.1节里给出的汽车参数即可算出图5.4.1中所示的横向加速度－质心侧偏角图，前提是汽车行驶在半径不变的圆周上。
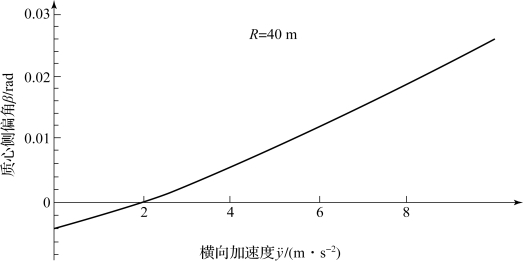
图5.4.1 稳态圆周行驶的横向加速度－质心侧偏角图
每辆只用前轮转向的汽车在横向加速度为零时的质心侧偏角都不等于零，这个角度被定义为负值。随着速度的上升，质心侧偏角将逐渐变为零，然后呈非线性增长。
这里所说的υ＝0时质心侧偏角为负值是“阿克曼汽车”的一个典型表现。
汽车界里对于质心侧偏角在评判汽车性能的意义上颇有分歧，质心侧偏角被定义为汽车纵轴与它行进方向的夹角，而这两个方向都不能直接得到。另外，质心侧偏角在一般的行驶状态下最大也只有几度。驾驶员将如何感知这个值，至今在感官学上还没有得出定论。而且，从另一个角度来讲，质心侧偏角很容易从汽车动力学理论算出，却很难测出。尽管有这么多的疑问，我们还是要继续研究这个值，因为它在学术讨论中占有很重要的地位。
由阿克曼先生提出的汽车模型的车轮不具有侧偏角（αV＝αH＝0）。从图5.4.2的几何关系得到前轮的转向角
δVA＝（a＋b）χ 当 R＝1／χ≫a＋b
这个“阿克曼转向角”δVA在转向半径不变的情况下不随速度改变，如图5.4.3所示。
上边所说的这种特征，每辆汽车在速度υ＝0时也有，运动的瞬心位于后轴的延长线上。可是真实的汽车在行驶时前后轴上却有侧偏角，也就是说车轮的轮平面与行驶方向不一致。图5.4.2就展示了这种几何关系。
图5.4.2（a）中
αV＝αH＝0，β＝βA＝bχ，δV＝δVA＝（a＋b）χ
图5.4.2 运动标量和转向角
（a）阿克曼汽车；（b）一般情况
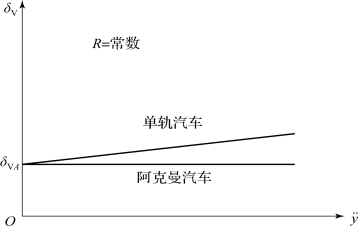
图5.4.3 不足转向汽车横向加速度－转向角图
脚标“A”＝阿克曼值。
图5.4.2（b）中
△ACMp：
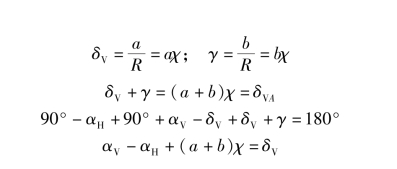
△ASPMp：
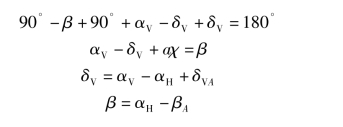
其中
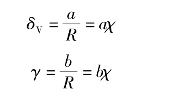
即得到
δV＋γ＝（a＋b）χ＝δVA
从一般情况（b）中的两个三角形得出
式中 βA——阿克曼汽车的质心侧偏角。
为了找到真实汽车的转向角与轮胎参数之间的关系，不仅要建立v·＝0、φ·＝0及FW＝0时横向力的平衡方程，而且还需要建立绕垂直轴的力矩平衡方程，即(www.xing528.com)
因此 
由此得到后轴的侧偏角
从式（5.4.4）和式（5.4.5）推导出
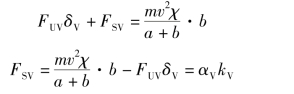
得到前轴的侧偏角
将式（5.4.7）代入式（5.4.2）得到前轴的转向角
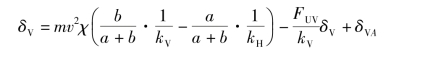
或者写成
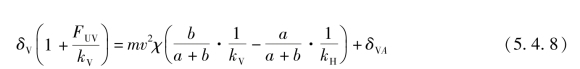
其中，
（前轮驱动）或者
（后轮驱动）。
对一辆后轮驱动的汽车来讲，kV≫kH，转向角随着横向加速度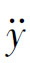
＝v2χ呈线性上升。
实际中的汽车具有非线性的轮胎特征，侧偏刚度随着车轮载荷的改变而改变。转弯时，同一根轴上的两个轮子在轮载荷很大时具有非线性的侧偏刚度，而这个侧偏刚度是可以利用横向稳定器有目的地改变的。
图5.4.4显示了等半径转弯时横向加速度－转向角在一般规律下的关系。
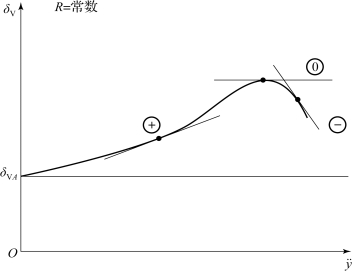
图5.4.4 等半径转弯时横向加速度－转向角的关系图
横向加速度在0.4g以下时，转向角随着横向加速度呈线性上升，即kV和kH还在常数区域之内，而且轮胎的侧偏刚度还保持常数。
“过多转向”“不足转向”和“中性转向”根据图5.4.4很容易定义出来：
切线的斜率就是转向趋势最好的标尺。
因为某些测试并不是等半径进行的，阿克曼转向角也会改变，所以稳定性因数依照DIN 70000一般性地定义为
式中 is——转向系的比例系数；
δL——方向盘转角；
δA——阿克曼转向角；
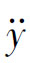——横向加速度。
因此有 
实际中的汽车在转弯时的反应如图5.4.5～图5.4.8所示，摘自HeiBimz（1982）。
图5.4.5 实验汽车参数
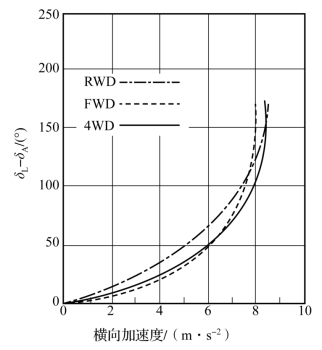
图5.4.6 方向盘转角δL和阿克曼方向盘转角δA之差，以横向加速度为变量，不同的驱动方式，稳态圆周行驶R＝40 m，干燥路面
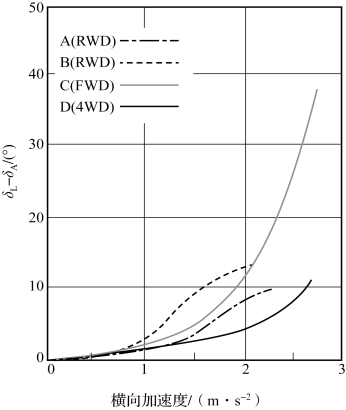
图5.4.7 方向盘转角δL和阿克曼方向盘转角δA之差，以横向加速度为变量，不同的驱动方式，稳态圆周行驶R＝45 m，结冰路面
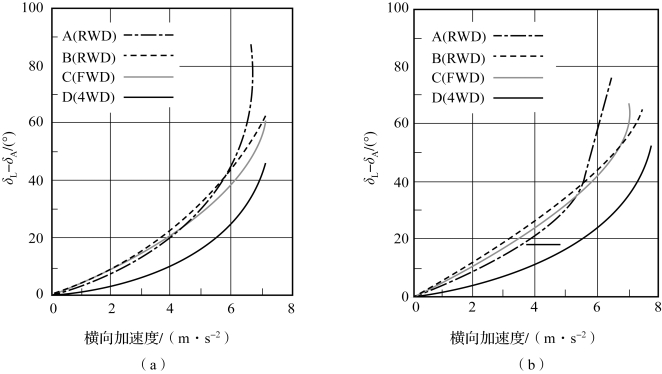
图5.4.8 方向盘转角δL和阿克曼方向盘转角δA之差，以横向加速度为变量，不同的驱动方式，稳态圆周行驶R＝100 m
（a）潮湿路面；（b）干燥路面
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
