车辆系统仿真：解非齐次微分方程

从非齐次微分方程里既能解出转向角或侧向风的干扰引起的汽车的运动过程，也能解出传递函数。

这里，可以在式（5.1.17）、式（5.1.18）以及式（5.1.20）和式（5.1.21）基础上解出不同的传递函数。

再次从谐振激励出发，选择下面的假设解：

上式中带“⌒”号的量是复数振幅。

设s＝jω，并且将分子部分缩略为

即得到横摆和质心侧偏角的传递函数

由于

因此

侧向风作为激励时，有以下传递函数：

当然，固有频率与阻尼量仍然保持不变，和齐次方程解出的一样。

无阻尼固有频率为

雷氏阻尼量为

在ω＝0，即s＝0时，增益

即稳态转向行驶时的增益值按照不同的转向角而变化。

在推导出了传递函数的表达式之后，就可以将典型激励函数的响应以及时间域变化计算出来。典型的激励之一就是阶跃函数，我们选它作为转向角激励函数λ（t）＝1·σ（t）。在实际生活中驾驶员基本只会如此跳跃性地改变转向角，因为这样转向角速度将无穷大。一般来说，驾驶员只会斜坡式地改变转向角，即转向角速度最大为600～700 rad／s，直至达到某一个固定值。如果这个过程是从直线行驶开始，则可以看作开入一个圆形车道的过程（以跃变式或斜坡式的转向角激励）。作为侧向风激励，我们选择脉冲FW（t）＝1·δ（t），它在实际中相当于极强劲的阵风。另外，我们还选择了以下参数：

m＝870 kg，e＝0.3 m

Θ＝1 146 kg·m2，FW＝1 0003 N

a＝0.8 m，b＝1.5 m

υ＝35 m／s＝126 km／h，kV＝5.6×104 N／rad，kH＝6.6×104 N／rad

从图5.3.1中，我们能清晰地辨认出汽车的有阻尼固有振动。自然，汽车所有的状态值及它们的导数都具有同样的固有频率和阻尼值。质心侧偏角响应开始有一小段是负值，然后不久就转成正值。这说明，一开始前轮的侧偏角大于后轮，在零值区域两个侧偏角相等，继而后轮的侧偏角就大于前轮了。侧偏角在大约1 s之后达到一个稳定值，此时汽车就处于稳态转向行驶状态。

图5.3.1　质心侧偏角β以及质心侧偏角速度对转向角阶跃δV（t）＝σ（t）响应的时间域曲线

质心侧偏角很容易分析计算出来，但测量却很麻烦。它从定义上讲是汽车行驶方向与汽车纵轴间的夹角，通常是直观地从汽车纵向和横向的加速度测出这个状态值。理论上讲只有将传感器安装在汽车重心正下方才能准确地测量，但是一般情况下重心下面是没有位置安放传感器的。如果在汽车的侧面或后部测量，则测出的纵向和横向速度在进入稳态的瞬时过渡过程中就会有误差，原因在于测量处汽车转动的切向分量。

图5.3.2中汇总了3个角速度受转向角阶跃激励的结果，图5.3.3则展示了3个角的时间域变化。如上所述，行驶方向角和横摆角随时间线性增大，因为汽车在1 s之后就从稳态转向行驶状态了，而质心侧偏角则保持常数。

图5.3.4是图5.3.3的一个局部放大。我们看出，行驶方向角和横摆角并不是从一开始就是平行的，而是在t＞1 s之后，这两个角通过质心侧偏角相互关联。

从图5.3.5和5.3.6中能够看到汽车对转向角谐振激励的反应。例如。在相同振幅和不同的激振频率下，汽车受低频率转向角激励时横摆角和行驶方向角变化较大。这个结论是合理的，因为这个情况正对应了和缓的转弯，质心侧偏角在频率域上基本保持不变。当频率很高时，所有3个角对激励都不敏感，也就是说它们的振幅与激励振幅之比以不同的斜率趋近于零。图5.3.6中3个角速度的趋势却完全是另外一个样子。横摆角速度在高频区域也趋向于零，但行驶方向角速度和质心侧偏角速度却保持常数。

(www.xing528.com)

图5.3.2　角速度，和对转向角阶跃δV＝σ（t）响应的时间域图像

图5.3.3　角φ，v和β对转向角阶跃δV＝σ（t）响应的时间域图像

图5.3.4　角φ，v和β对转向角阶跃δV＝σ（t）响应的时间域图像的局部放大

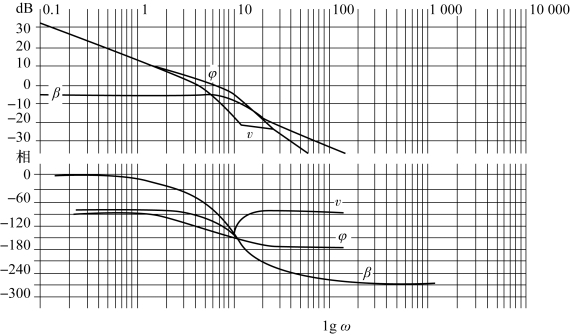
图5.3.5　传递函数Hβ／δ，Hv／δ，Hφ／δ的伯德图

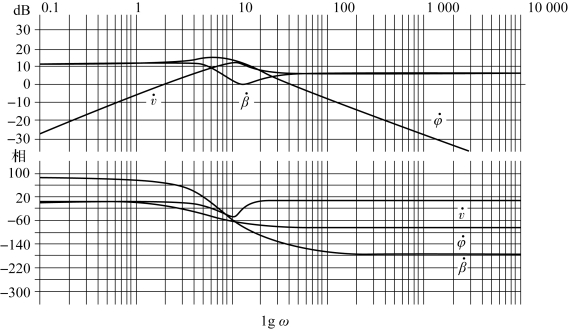
图5.3.6　传递函数Hβ·／δ，Hv·／δ，Hφ·／δ的伯德图

图5.3.7是谐振作为侧向风激励函数的伯德曲线。等风力振幅的低频率激励导致行驶方向角和横摆角速度做等振幅振动或者振幅随频率的升高而降低，后者在这里没有给出。行驶方向角和质心侧偏角振幅在高频区域也遵循同样的规律。

如果现在汽车受到一阵强烈的侧向阵风，就会出现图5.3.8所示的时间域曲线。质心侧偏角和行驶方向角在此影响下跃变到某一个特定值，在大约1 s之后汽车将以新的行驶方向角及新的横摆角向着另一个方向前进。而质心侧偏角从这一刻开始却重新恢复到零。在这个过程中，汽车的固有频率和阻尼值也和受转向角激励时的相同。

需要特别指出的是，这样的时域变化过程不能当作衡量驾驶员－汽车系统的侧向风敏感性的绝对尺度。首先，侧向风敏感性的一部分是通过测量汽车驶过人工侧向风装置的结果得出的，而其过程是开环测试，即驾驶员完全不参与控制过程。这种人工侧向风装置通常是由平行设置的鼓风机组成的。方向盘紧握不动，汽车在侧向风作用下驶向一侧。某一固定地点的侧向偏离长度被记录下来，而驾驶员－汽车系统的侧向风敏感性则来自汽车的空气动力学特征和它在直向行驶干扰下的横向动力学特征，这个直向行驶干扰是通过改变转向角引起的。

图5.3.7　传递函数Hβ·／FW，Hv·／FW和Hφ·／FW的伯德图（振幅响应向上推移了＋100 dB）

图5.3.8　角φ，v和β对侧向风脉冲FW（t）＝δ（t）响应的时间域图像

在考虑某些问题时，汽车的曲率也会很有用处。在式（5.1.17）里通过以下关系引入横摆角φ＝v＋β以及，并由汽车的重心绕瞬心运动的公式

得出传递函数

或者

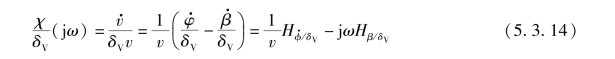
这里列出两种比较特殊的情况，如图5.3.9所示。

图5.3.9　以速度为变量的曲率与转向角的商值曲线

（1）激励频率ω＝0即δV＝常数，这种情况即为稳态圆周行驶，式（5.1.13）简化为

将常数a11、a22、a12、a21、b1和b2的值代入上式，并且令FUV＝0，则

极端情况，即υ≈0时，有

如果一辆汽车满足υ≠0，且kV a＝kH b——这可以通过“强行滑动”法将适当的切向力分配到后轴上来做到——同样可以令χ／δV＝1／（a＋b）从而达到所需的曲率和弯道半径，绝对与速度无关。具有这种特征的“阿克曼汽车”下面还会提到。

（2）如果激励频率ω很高，即ω相对于ω2可以忽略不计，则式（5.1.13）变为

所以，高频率时，曲率随着速度的增大而呈双曲线式地减小。