横向运动方程组在车辆系统仿真中的应用

图5.1.1所示就是一个单轨模型。

图5.1.1　单轨模型的运动状态值、受力和力矩分析（俯视图）

横向运动的单轨模型具有以下前提。

（1）模型在它所处的平面上具有3个自由度。

（2）根据模型的单轨特性，在前后轴上分别只有一个轴载荷，而且它位于轴的中心。

（3）转弯时重心受的侧向力与车轮受的侧向力相平衡，车轮侧向力导致车轮侧向偏离——即车轮平面与车轮的前进方向成α角，侧向力与侧偏角的比率称为侧偏刚度。

（4）侧偏角小于5°的范围内，侧向力随侧偏角线性上升，也就是说，在这个范围内侧偏刚度为常数。

（5）驱动力能够满足行驶阻力。

（6）在小角度内（横摆、转向及质心侧偏角很小）保持线性关系，因为此时转动半径相对来讲很大。

前轴和后轴分别有图5.1.2所示关系。

图5.1.2　前后轴上的转角和运动矢量

图5.1.1和图5.1.2中标记定义为：1／χ为弯道半径，FW为风力，β为质心侧偏角，MW为风力矩，δV为前轮转向角，FSV，FSH为侧向导向力，φ为横摆角，FUV，FUH为切向力，υ为行驶方向角，v为车速。

行驶方向角υ定义为汽车的运动方向与某一特定参照方向之间的夹角；横摆角φ则定义为汽车的纵轴与这个参照方向的夹角。它们的差恰好就是质心侧偏角β。

对纵向应用质心定理，有运动方程为

对横向应用质心定理，有运动方程为

对绕穿过重心的垂向轴应用惯性矩定理，有运动方程为

由于侧向力在侧偏角小于5°时与它呈线性关系，存在

kV和kH为侧偏刚度（侧偏角很小时的比例系数）。

从图5.1.2中得出小角度关系为

将式（5.1.5）代入式（5.1.4）得出

另外，＝vχ，或者说。(www.xing528.com)

从图5.1.1中能看出，横摆角、行驶方向角和质心侧偏角之间存在着以下关系

从中解出曲率

现将式（5.1.6）～式（5.1.8）代入式（5.1.1）～式（5.1.3）中，运用小角度假设，忽略空气阻力的影响，即设FW＝MW＝0，就有

这组相关方程依然是非线性的，线性化的方法是设行驶速度为常数（即υ＝0），使得常数υ、kV、kH、a、b、m和Θ成为的系数，即

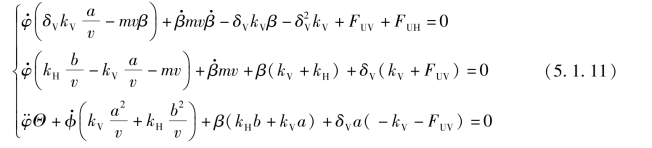
图5.1.3为汽车横向动力学参数模型。

图5.1.3　汽车横向动力学参数模型

速度υ，侧偏刚度kV和kH，重心位置a和b，汽车质量m以及惯性矩Θ的值都必须是已知的。

式（5.1.11）的第一个等式只描述了纵向力之间的关系，因此不必进一步加以讨论——至少在后轴驱动（FUV＝0）时能够这么做。这样，就只剩下两个相关方程——横向运动和转动。在横向动力学里它们是至关重要的。建立横摆角和质心侧偏角方程：从式（5.1.11）的后两个方程里推出一个非齐次二次方程。为了表达方便，将方程中的系数用a11、a12、a21、a22、b1和b2来代替，即

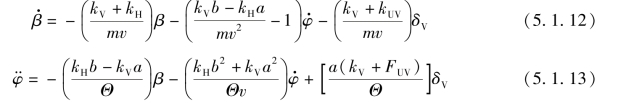
因为kV≫FUV，所以纵向力不会影响横向运动。正如式（5.1.11）的第一个方程所述，它只用来抵消行驶阻力。各系数的表达式为

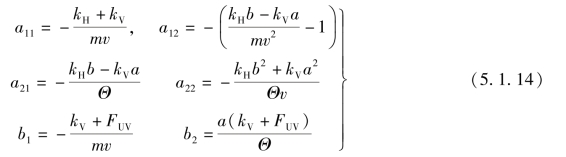
因此，得出相关方程

这个方程组可依照前文的矩阵法解出，或者按照传统方法将一个方程变形整理后代入另一个方程。例如，将式（5.1.16）按照β整理后求导，得到的表达式，然后代入式（5.1.15）中，就得到φ的表达式，而这个表达式只与δV，以及常数有关，即

这是一个φ的非齐次三阶微分方程，里面缺少关于φ的那一项。

将设成φa，方程就变为

这是一个关于φa的典型二次振动微分方程，左边是φa，右边是转向角引起的振动。通过同样的分析也能够得到一个关于β的微分方程，即

式（5.1.18）和式（5.1.19）都是线性非齐次的二阶微分方程（条件是行驶速度υ与时间t无关）。它们在形式上与前面讲的单自由度系统的微分方程相同，而且两个式子左边各项的系数分别相同。

表达式a11 a22－a12 a21对应着单自由度系统的弹性系数与质量的商，即无阻尼固有频率；而－（a11＋a22）则对应着阻尼量。尽管在单轨模型里没有真正的弹簧与减振器，但轮胎本身的特性还是造成了阻尼和弹性刚度。由此证明，所有的横摆角、质心侧偏角和行驶方向角都源于同样的固有频率和阻尼。如果汽车的运动不是由转向角，而是由侧向风激励的话，那么表达式将变成下面形式：

分析方法和式（5.1.15）、式（5.1.16）以及式（5.1.18）、式（5.1.19）相同，唯一的不同点是激励方式不一样。