汽车瞬态过程：车辆系统仿真实践

加速或制动时会产生惯性力，其作用点是整个汽车与车内人员的总重心。前面计算时针对的都是制动很久以后所达到的稳态，如果没有制动防抱死装置，瞬时状态中往往会出现极其危险的单轮过度制动。下面将详细计算一辆汽车的垂向和俯仰运动、动态轮载荷和制动切向力，并绘出它们的时间图。

图4.4.1为带有车桥的汽车模型简图，从中能清楚地看到架在纵拖臂上的前悬和后悬，轮毂与俯仰瞬心之间的粗虚线代表了纵拖臂。为了不损伤普遍性，俯仰瞬心和重心特意绘在不同的位置。建立运动方程的方法多种多样，尽管拉格朗日法在计算上比较优越，但这里还是应用一般的牛顿原理，因为它在分析时层次比较清楚。首先进行系统分析，然后再对每一个分系统进行受力平衡分析，分析结果如图4.4.2所示。

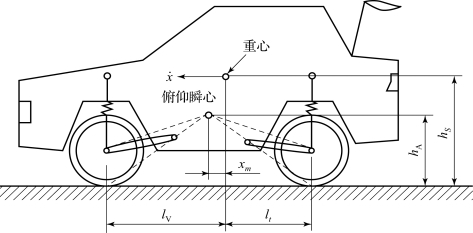
图4.4.1　带有车桥的汽车模型简图

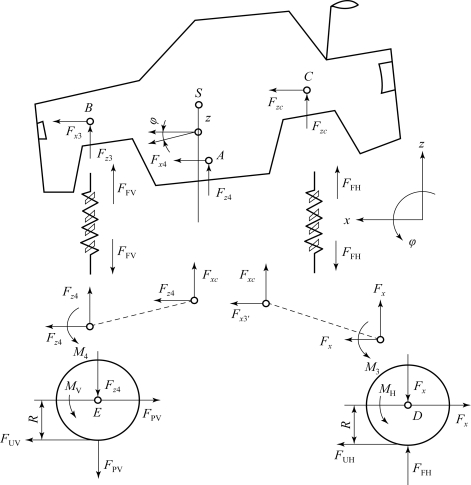
图4.4.2　非平衡状态下的系统分析

各部分的力与力矩平衡（所有的路程差都相对重心而言），对前轮有

对后轮有

对前悬有

Fx4′＋Fx4＝0，Fz4′＋Fz4＝0，M4＋Fx4′（zA－zE）－Fz4′（xA－xE）＝0

对后悬有

Fx3′＋Fx3＝0，Fz3′＋Fz3＝0，M3＋Fx3′（zA－zD）－Fz3′（xA－xD）＝0

对车架（设P点为车身质心）有

各个力的大小如下：(www.xing528.com)

（kV为前悬刚度系数，cV为前悬阻尼系数）

（kH为后悬刚度系数，cH为后悬阻尼系数）

车轮平动与转动的关系为

前轮、后轮和车架这3个分系统有各自的纵向加速度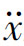1、2和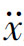，这3个量却通过悬架系统与车身的动力学关系相互联系在一起。若重心既向上抬起z，又转过角φ，车轮中心则会做相应的运动。这种联系被称为运动边界条件，它将整个运动问题转化为了一组线性微分方程，导出的结果是一组非线性方程组。以平衡时车身重心为参考点和初始坐标，经动态分析可得车架的线性化相关运动方程。

纵向运动方程为

垂向运动方程为

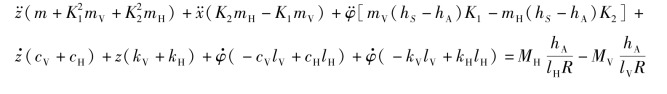
俯仰运动方程为

其中

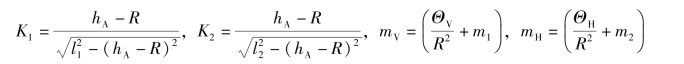
方程之间的相关性说明，加速和制动会同时引起纵向、垂向和俯仰运动。整个瞬态过程据此微分方程模型可进行求解计算。