忽略了转动惯量、滚动阻力、空气阻力和爬坡因素之后,得到一个总体的简化了的切向力关系和附着率关系。进一步将切向力、加速度、附着率和汽车的参数联系起来,并在一个图中展示出来,我们就不仅有了一个确定制动系统性能的有力工具,而且可以极简便地分析驱动力分配,这样的一个图像被称为切向力图。
按照式(4.1.4),有

由式(4.3.2)和式(4.3.3)推出轮载荷公式为

另外,还有附着率关系公式为

取FUV/FG和FUH/FG作为切向力图的坐标轴;而且横轴向左是FUV的正方向,纵轴向下是FUH的正方向,如图4.3.5所示。这种设定坐标轴的方式与习惯上的设定方式相反,原因是,切向力图从根本上讲是为分析制动而画的,制动时的切向力为负值。
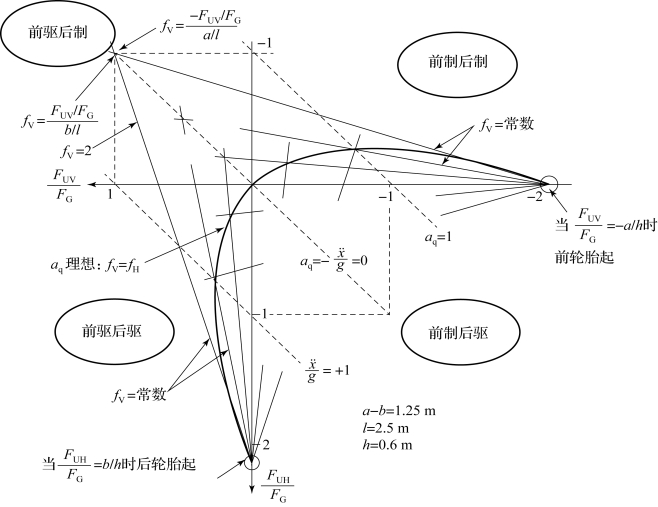
图4.3.5 切向力图
这样,就围出一个区域,在它上面可以表示出所有切向力造成的加速度或减速度。从式(4.3.22)可知,切向力与加速度之间的关系在图上是一根直线,它与轴的交点值就是![]() 的值。
的值。
将式(4.3.23)和式(4.3.24)代入式(4.3.22),即有
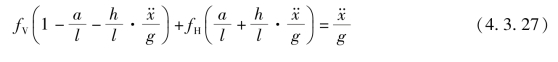
或
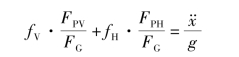
此式表达了一辆特定的汽车所有的行驶状态,决定性的参数是它的重心位置a和h与轴距l之比,甚至包含前轮驱动同时后轮制动的情况。
制动强度或驱动比的等值线是从(FUV/FG)+(FUH/FG)=-aq得出的(如45°线——与两轴交点值相同的直线)。(https://www.xing528.com)
当一辆车猛烈地加速或制动,以至使一个轮离地而起,即FPH=0或FPV=0时,切向力无法再生效。加速时,若![]() ,即式(4.3.23)中括号里的表达式的值为零的时候,前轮的切向力就会为零;制动时,后轮的轮载荷FPH会减到零,使得FUH=0。这时,
,即式(4.3.23)中括号里的表达式的值为零的时候,前轮的切向力就会为零;制动时,后轮的轮载荷FPH会减到零,使得FUH=0。这时,![]() ,即式(4.3.24)括号里的表达式的值为零。当然,这样说的前提条件是,假设地面的摩擦系数近乎无穷大。
,即式(4.3.24)括号里的表达式的值为零。当然,这样说的前提条件是,假设地面的摩擦系数近乎无穷大。
等附着率(fV=常数)是呈放射状的直线组,它们相交于纵轴上的FUH/FG=b/h,因为前轮抬起而且FUV=0和fV无关。确定这些线条的第二个点是它们和 /g=0(即aq=0)的交点,因为在这些线上fV=(FUV/FG)/(b/l),同样可以画出fH=常数的直线组:横轴的起始点为FUV/FG=-a/h,因为此时后轮由于强烈制动而抬离地面,FUH=0;第二个交点在aq=0上,借助公式fH=(FUH/FG)/(b/l)。
/g=0(即aq=0)的交点,因为在这些线上fV=(FUV/FG)/(b/l),同样可以画出fH=常数的直线组:横轴的起始点为FUV/FG=-a/h,因为此时后轮由于强烈制动而抬离地面,FUH=0;第二个交点在aq=0上,借助公式fH=(FUH/FG)/(b/l)。
至此,所有用以确定汽车直线运动动态性能的“外界参数”就都清楚了。
理想制动及理想驱动曲线假设由所有满足fV=fH的交点组成,并假设它的形状是一条向斜下方张开的侧抛物线,且穿过原点和前后轮载荷等于零的点。轮载荷等于零时的切向力可以分别从式(4.3.22)~式(4.3.27)导出,即

也可将FUV变为 /g的表达式,即
/g的表达式,即
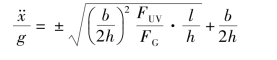
代入式(4.3.22)得

这就是图4.3.5里那条理想切向力分配的抛物线,它只受重心参数b=l-a及h的影响。
从式(4.3.28)看出,FUV的零值点在 /g=0和
/g=0和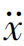 /g=b/h,FUH的零值点在
/g=b/h,FUH的零值点在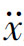 /g=0和
/g=0和 /g=a/h。后边这两个数值即是前面提到过的轮抬起的时刻,此时FUV和FUH分别达到极大值,即
/g=a/h。后边这两个数值即是前面提到过的轮抬起的时刻,此时FUV和FUH分别达到极大值,即
当![]() 时,有
时,有
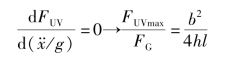
当 时,有
时,有

据图4.3.5,可直观分析汽车驱动力和制动力的分配问题,详细实例见参考文献[1]。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




