车辆加速行驶时，会受到整车质量的惯性力的阻碍，该惯性力叫作惯性阻力，以Fgx表示。
车辆的质量分为两种：一种是车体和装在车体上面所有装置一起做平移运动的质量；另一种是和驱动轮有运动学联系的做旋转运动的旋转质量。车辆加速行驶时，平移质量产生惯性力，旋转质量产生惯性力矩。要准确计算每一项都比较麻烦，通常是将旋转质量也当作平移质量来计算惯性力，并以δ作为换算系数（δ＞1）。所以，惯性阻力可用下式表示：
式中 G——重力（N）；
g——重力加速度，g＝9.8 m／s2；
m——车辆全质量（kg）；
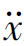——车辆加速度（m／s2），
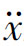＝d v／d t；
v——车体行驶速度（m／s）；
δ——质量增加系数。
下面讨论如何求出δ的表达式。
车辆加速行驶时，平移质量做牵连运动（平移运动），其速度为v＝vq；旋转质量相对车体做相对运动（旋转运动），其速度为vx。一般路面条件下，滑转系数σ较小。这里假设滑转系数σ＝0，vx＝vq＝v。则车辆直线行驶时的总动能
Eq——牵连（平移）运动动能，且
Ex——相对（旋转）运动动能，且
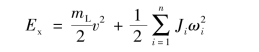
式中 mL——履带环或全部车轮的总质量（kg）；
Ji——第i个和驱动轮有动力联系的旋转零件的转动惯量（kg·m2）；(www.xing528.com)
ωi——第i个和驱动轮有动力联系的旋转零件的角速度（rad／s）。
假设第i个旋转零件和驱动轮间的传动比为ii，驱动轮的角速度为ωz，所以ωi＝iiωz，又知ωz＝v／rz，因此ωi＝ii v／rz，可得
如前文所述，车辆是平移质量为m，并且是有内部旋转质量的物体，加速时其质量相当于增加了δ－1倍，所以车辆直线行驶的全部动能应为
将式（4.2.19）～式（4.2.21）代入式（4.2.22）并整理得
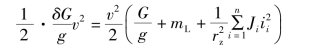
变化上式可得质量增加系数δ的数学表达式为
质量增加系数δ的物理意义是车辆总动能E与牵连运动动能Eq的比值。质量增加系数δ是一个大于1的正值。从式（4.2.23）中可以看出，质量增加系数δ主要受到以下因素的影响：
（1）随履带或车轮质量的增大而增大；
（2）随各旋转零件的转动惯量的增加而增大；
（3）随着与驱动轮有运动学联系的旋转零件数目n的增多而增大；
（4）随着传动比ii的增加而增大。
质量增加系数δ从理论上计算是比较困难的。实际工程中，多采用实验法测量δ值。某些坦克的质量增加系数δ的实验值如表4.2.5所示。从表中数据可以看出，这些坦克的质量增加系数δ为1.2～1.43。
表4.2.5 某些坦克的质量增加系数实验值
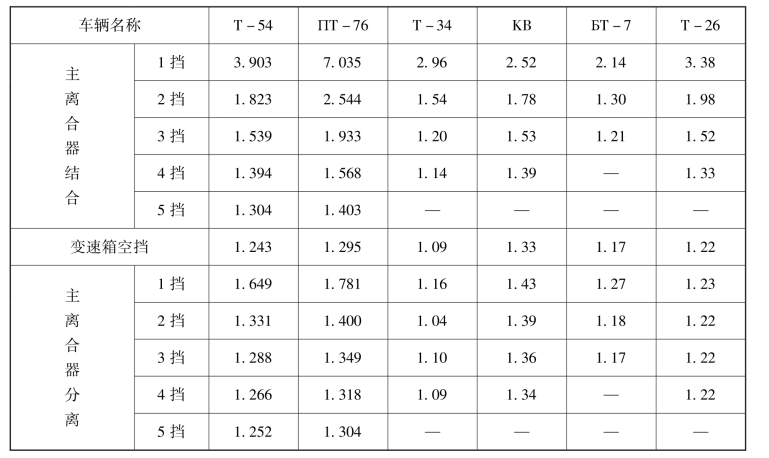
注：此表取自＜ТЁОРИЯ ТАНКА＞А.О.НИКИТИН，Л.В.СЕРГЕЕВ.1962.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
