建立质量弹簧－人－座椅系统3自由度系统，如图3.3.1所示。此3自由度振动系统的运动方程为
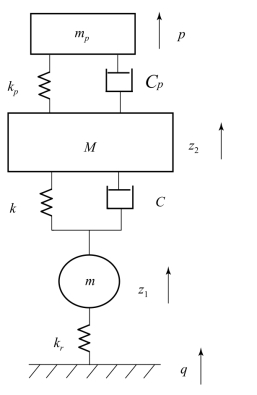
图3.3.1 3自由度系统
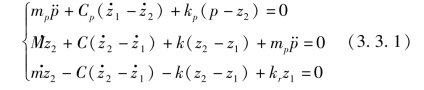
3自由度系统可分成两个环节，一者为双质量（M～m）系统，二者为一单自由度的人－椅系统。由于两个环节之间并无反馈作用，因此该系统是前一环节的输出为后一环节的输入的串联系统。这种串联系统的幅频特性是两个串联环节幅频特性之积，即
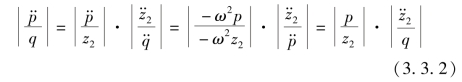
所以，我们就得到了人承受振动加速度的功率谱密度S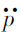
（f），如图3.3.2（d）所示，且有(www.xing528.com)
分析图3.3.2可知，当激振频率
时，为人－椅系统减振区，即随ω的增加，振动幅值小于车体的激励幅值，而且越来越小。所以，为了人－椅系统能充分隔离人最敏感的4～8 Hz频率范围的振动，其固有频率ωp的选择十分关键。由于
必须小于4 Hz，若以等于4 Hz为上限，则
。图3.3.2（b）就是选择ωp／2π＝3 Hz，说明当激振频率大于
时，系统就处于减振区了，所以4～8 Hz的振动得到了必要的衰减，比较图3.3.2（a）和图3.3.2（c）可见其衰减效果。然而，在人－椅系统共振区，出现了共振峰，把车体的振动放大了一倍左右。在选择ωp时，除了上述衰减4～8 Hz振动的要求外，还必须注意ωp不能和车体的自然频率相重合，即ωp≠ωn。如果ωp等于ωn，则车辆振动的第一阶共振峰就得被放大，出现更大的尖峰，显然这对车辆的行驶平顺性极为不利。对地面车辆而言，由于车体的自然频率多在1.2～1.5 Hz，故人－椅系统的自然频率也应选择在1.5≤fp≤s，通常选2～3 Hz。
根据人－椅系统自然频率的确定原则，可否使fp＜f？请读者研究。由图3.3.2（c），即人体的加速度响应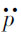
对地面激励幅值q的幅频特性可见，在系统的共振区出现了峰值，显然其峰值的大小取决于系统的相对阻尼φp值，通常取φp＝0.25。φp值的选择，一方面要考虑共振峰值不可太大，另一方面还要考虑在高频区也有良好的减振效能。
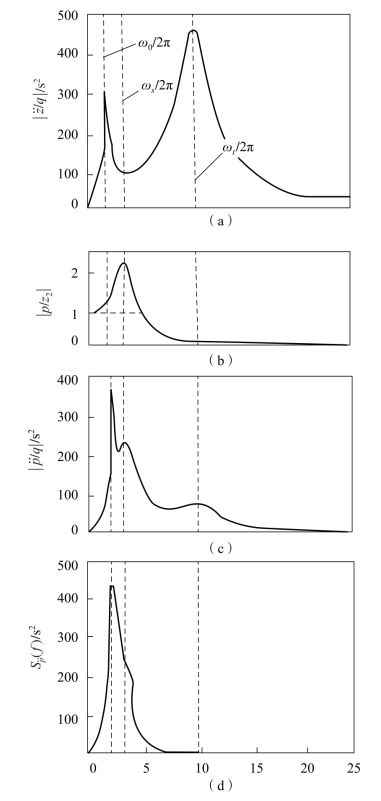
图3.3.2 人－椅系统特性
（a）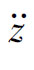
～q的幅频特性；（b）p～z2的幅频特性；（c）
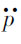～q的幅频特性；（d）人体承受加速度
的功率谱密度
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
