履带车辆振动模型：车辆系统仿真理论实践

履带车辆车体的振动，实际上是复杂的，严格地说是一个具有6个自由度的振动系统，如图3.2.9所示。通过车体重心作一X、Y、Z的空间坐标，则可以看出，车体的振动可以分为沿X、Y、Z轴的线振动和分别绕该轴的角振动，一共6种振动。

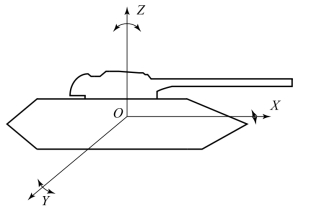
图3.2.9　6自由度的车体振动

现对6个自由度的振动分别加以具体分析，略去一些次要的振动，以便能更好地分析和讨论履带车辆车体的振动规律。事实表明，由于车辆悬挂构造的限制，一般沿Y轴、X轴的线振动和绕Z轴的角振动较不易发生或较不明显。此外，如果车辆左右侧所遇到的地面起伏情况大致相同，则绕X轴横向角振动也比较小。因此，本书只讨论车体沿Z轴的垂直线振动和沿Y轴的纵向角振动。

车体振动可以分为自由振动和强迫振动。自由振动是指引起振动的外力停止作用后，仅有弹性恢复力的作用时的振动。例如，车辆驶过地面一个凸起后，车辆便做自由振动。但实际上这种振动由于振动系统中有阻尼存在，会逐渐减小以至消失。当车辆在不平地面上行驶时，路面不平度引起的外力不断地作用在振动系统上，这样的振动称为强迫振动。所以，车体振动实际上是一种具有阻尼的强迫振动。

设履带车辆在振动过程中，其悬置车体相对其静平衡位置，既有向下垂直位移z，又同时绕通过其重心的横轴向后旋转一个角度φ，如图3.2.10所示。

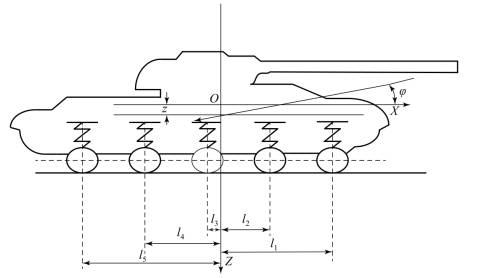
图3.2.10　履带车体振动简图

车体由静平衡位置向下移动的位移取为正值，车体角位移由静平衡位置向后转动（即车尾向下）时取为负值；由重心到前面各负重轮轴心的距离为正值，而到后面各负重轮轴心的距离为负值。并假定作用在车体上的弹性恢复力矩，顺时针方向为正，逆时针方向为负。

现建立履带车辆车体垂直线振动和纵向角振动的微分方程式。当履带车辆处于静平衡状态时，车辆的悬置重力和各弹簧的静变形弹性恢复力相平衡，重心左、右各弹簧静变形所引起的弹性恢复力矩也互相平衡。若履带车辆车体离开静平衡位置后，由于弹簧的附加变形而产生的附加弹性恢复力PT和弹性恢复力矩MT为

式中　PTi——离开静平衡位置时，各弹簧的弹性恢复力；

MTi——离开静平衡位置时，各弹簧的弹性恢复力矩；

n——履带车辆一侧负重轮数目。

根据动力学基本定律，可以分别写出履带车体重心垂直振动和车体纵向角振动的两个微分方程式为

式中　Mx——履带车辆的悬置质量；

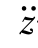——履带车体的垂直加速度；

Iy——履带车体绕通过其重心横轴的转动惯量；(www.xing528.com)

——履带车体在纵向平面内的角加速度。

设车体重心的垂直位移为z和车体转动角为φ，则第i个负重轮弹簧的总变形为

式中　z——车体重心的垂直位移；

φ——车体在纵向平面内的角位移；

li——重心到各负重轮轴心的距离，负重轮位于车体重心前的取正值，位于重心后的取负值。

由于

故

设各悬挂的刚度mxi均相同，取出总和符号内的常数，并将每个总和分成两部分，则可写成下列方程式：

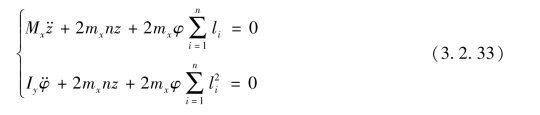
令

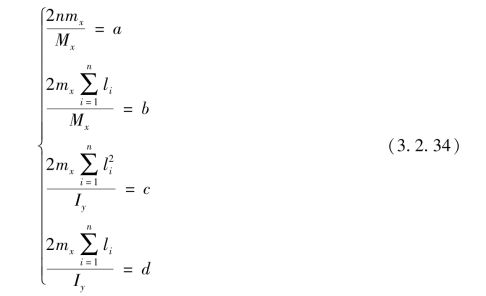
则履带车体重心的垂直振动和车体纵向角振动的微分方程式可以写为

从上面两个方程式中可以看出，在每个方程式中都含有变量z和φ，这说明在一般情况下垂直振动和纵向角振动互相耦合。当有垂直振动时必然引起纵向角振动，反之亦然。

添加路面激励的垂向振动模型为强迫振动微分方程，其建模可参考汽车垂向模型，以及履带车辆结构型式和参数来完成。同样地，垂直振动和纵向角振动存在相互耦合。