空间频率与时间频率功率谱密度函数的关系

车辆振动系统的输入激励除了与路面不平度有关，还与车速密切相关。在不平的路面上静止的车辆是不会产生振动激励的，车速越高产生的振动激励的强度越大。为了描述随时间t变化而变化的振动输入激励，需要根据车速v将空间频率功率谱密度Gq（n）换算为时间频率功率谱密度Gq（f）。

当车辆以一定车速v（单位为m／s）驶过空间频率n（单位为m－1）的路面不平度时，输入的时间频率f（单位为s－1）是n与v的乘积，即

可以看出，当空间频率n一定时，时间频率f与车速v成正比。功率谱密度的定义是单位频带内的“功率”（均方值），故空间频率功率谱密度可以表示为

式中，为路面功率谱密度在频带Δn内包含的“功率”。

在某一车速v下，与空间频带Δn相应的时间频带Δf内所包含的不平度垂直位移q的谐量成分相同，其“功率”仍为，因此换算的时间频率功率谱密度可表示为

将式（3.1.4）和式（3.1.5）代入上式，得到Gq（n）与Gq（f）的换算式为(www.xing528.com)

将式（3.1.1）、式（3.1.4）代入式（3.1.6），得到时间频率路面功率谱密度Gq（f）（单位为m2·s）表达式，当w＝2时，得

时间频率的不平度垂直速度和加速度的功率谱密度Gq·（f）（单位为m2／s）和Gq·（f）（单位为m2／s3）与位移功率谱密度Gq（f）的关系式为

由上式可知，时间频率的路面不平度位移、速度和加速度的功率谱密度函数Gq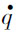（f）、G（f）、G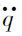（f）都与路面不平度系数Gq（n0）和车速v成正比。依据式（3.1.7）和式（3.1.8），通过傅里叶反变换就可以得到路面不平度位移、速度和加速度的时域激励信号模型。

在频域内，根据时间频率的路面不平度功率谱密度函数和车辆振动系统的传递函数H（f），可以很方便地求出各种振动响应量x（t）（如车身振动加速度、悬挂动挠度、车轮动载荷）的功率谱密度函数Gx（f）。由此可以分析车辆悬挂系统参数对振动响应特性的影响，反过来也可以根据车辆平顺性评价指标来优化车辆悬挂系统设计参数。