车辆系统仿真理论与实践-差分解法及适用范围

差分解法是对偏微分方程进行数值求解的常用方法之一，它是在时间和空间两个方面将变量离散化，进而得到一组代数方程，然后利用已给出的初始条件及边界条件逐个求解，则可将任一时刻、任一空间位置上的系统中的状态变量的值全部计算出来。

设有一条长为l的细棒，其侧面是绝缘的，t＝0时，温度分布为φ（x）。现将它两端接于温度为u1（t）及u2（t）的物体上，试计算不同时刻棒上各点处的温度。

这个问题的数学模型可以用下式来描述：

式中，K为导温系数，它取决于棒的导热系数、比热容和质量密度。为了解此方程，首先给出边界条件及初始条件。假定0≤x≤l，0≤t≤T，有

其中，式（2.4.2）为初始条件，式（2.4.3）及式（2.4.4）为边界条件。

差分解法的具体步骤如下。

（1）取时间变量t的步长为τ，将整个时间分为N份。取空间变量x步长为h，将整个长度分为M份。则在x－t平面上构成一个矩形网格，如图2.4.1所示。

图2.4.1　x－t平面上的矩形网格

图2.4.1中网格交点有

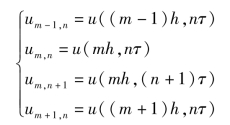
（2）以差分来代替微分，即

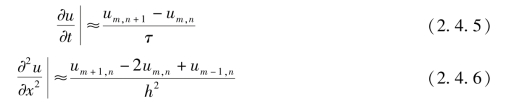
（3）将式（2.4.5）及式（2.4.6）代入式（2.4.1），则得

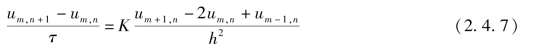
即

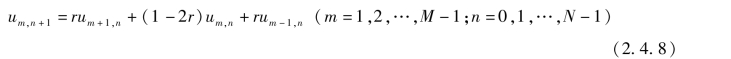
式中，。

（4）从t＝0开始计算（即从第1列开始计算），u0，0及uM，0如可由边界条件来确定，而中间各点um，0（m＝1，2，…，M－1）可由初始条件来确定，即

u0，0＝u1（0）

uM，0＝u2（0）

um，0＝φ（mh）

（5）然后计算第2列（n＝1）上各点的值，计算时，两端由边界条件来确定，而中间各点则由式（2.4.8）来计算，例如：

（6）然后计算第3列（n＝2），直到n＝N为止。

根据式（2.4.8）可以由第n个时间层推到第n＋1个时间层，该式提供了逐点计算um，n＋1的明显表达式，所以上述差分解法称为显式差分解法。

与显式差分解法相对应，还有隐式差分解法。若按下式计算：

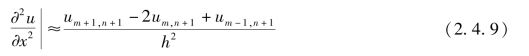
则式（2.4.7）将变成

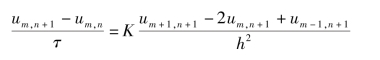
即

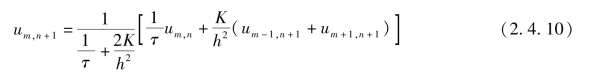(www.xing528.com)

由式（2.4.10）可知，为求um，n＋1不仅要知道um，n，而且要知道um－1，n＋1及um＋1，n＋1，因此要用迭代解法，上式即隐式差分解法。

采用差分解法时，若时间步长τ及空间步长h选择不合适也有可能产生数值计算发散的现象，即也存在稳定问题。

由式（2.4.7）可得

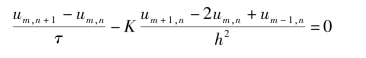
则误差εm，n应满足

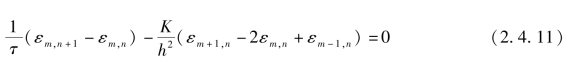
为不失一般性，现假设初始时刻的误差为

其中，k为频率参数，即波数，它是一个任意的实数，1／k称为波长。

为求出满足式（2.4.11）的εm，n，可先假设它为如下形式：

式中，λ（k）为对应于波数k的增长因子，简写为λ。

将式（2.4.13）代入式（2.4.11），得

消去公因子λn eikmh，可得

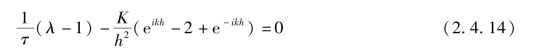
式（2.4.14）就是差分构成式（2.4.11）的特征方程，它的根为

式中，。

为保证误差不恶性增长，即保证计算稳定，要求特征根在单位圆内，即

由于计算中舍入误差是随机的，因此应该认为各种k的频率组合都是可能的，故式（2.4.16）应对一切实数k值均能满足。由式（2.4.16）可得

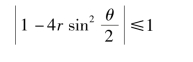
即

或写成

这说明，对显式差分解法，时间步长τ与空间步长h之间应有一定的比例关系。若为了提高精度将h减半，则根据式（2.4.18），τ要减小为原来的1／4，这样总的计算时间将加长8倍。可见，显式差分解法不适用于高精度的仿真计算。

类似地，可得到隐式差分解法的特征方程为

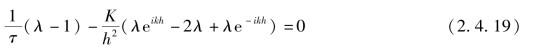
它的特征根为

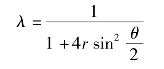
式中，。因此，不论k、τ、h为多少，都有，故隐式差分解法为恒稳的解法。