工程中绝大多数间断问题的数学模型都可以表示为式(2.3.1)的形式,即间断点能通过条件函数来判别。如果在仿真过程中,能够及时求出条件函数的零点,而后转换右函数由间断点重新开始积分,则可避免间断所带来的误差,具体步骤如下。
(1)用适当的积分方法由tn积分到tn+1,得到近似解yn+1,右端函数的状态由φn=φ(yn,tn)确定,转步骤(2)。
(2)计算条件函数φn+1=φ(yn+1,tn+1),判断条件函数是否改变符号。若符号改变,即φnφn+1<0,说明积分区间(tn,tn+1)中存在一个零点,转步骤(3);否则,令tn=tn+1,重复步骤(1)。
(3)利用适当的函数求零算法求出零点tz。
(4)对间断点进行处理。例如,由tn积分到tz得到y(tz)的近似值,或者利用插值求出其近似值。
(5)令tn=tz,转步骤(1)。
上面步骤(3)中不同的函数求零算法和步骤(4)中对间断点的处理方法就构成了间断问题的各种仿真算法,下面将分别介绍利用连分式求零和混合求零算法结合厄米特内插公式构造的两种间断性非线性系统的仿真算法。
1.连分式求零算法
假设已知条件函数零点tz附近的若干数据点{ti}上的条件函数{φi},则t可以考虑为φ的一个函数t(φ),将它表示成连分式展开式,即
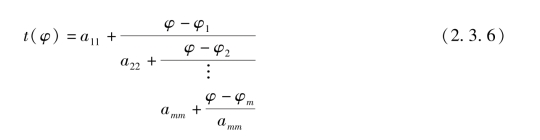
式中

在式(2.3.6)中,令φ=0,得到零点的近似值

一般来说,数据点越多,则零点的逼近程度也就越高。可以看出,式(2.3.7)和式(2.3.8)具有很好的递推性质,而且计算也比较简单。另外,还可以进一步对式(2.3.7)和式(2.3.8)进行简化,以改善其计算的稳定性。
下面考虑如何得到数据对(ti,φi),i=1,2,…,m。假定φi、φi+1已知,而且可以计算得到![]() ,其中
,其中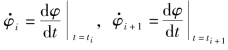 。于是,可以用如下的厄米特内插公式来表示φ(t),即
。于是,可以用如下的厄米特内插公式来表示φ(t),即
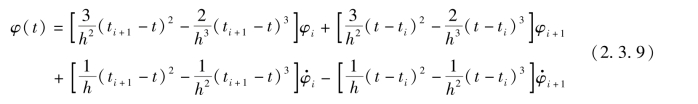
式中,h=ti+1-ti为积分步长。令![]() (m=1,2,…,n-1),有
(m=1,2,…,n-1),有

把式(2.3.10)代入式(2.3.9),得到定点简化内插公式,即

由于式(2.3.11)中的系数可以预先计算,因此式(2.3.11)可以在仿真过程中很快计算出来。例如,令n=4,则m=1,2,3,于是
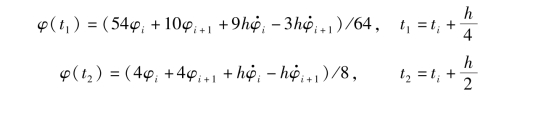
 (https://www.xing528.com)
(https://www.xing528.com)
另外有φ(ti)、φ(ti+1),共得到5个数据对,所以利用式(2.3.7)和式(2.3.8)可求出条件函数的零点tz。
如果在式(2.3.9)中用![]() 替换
替换![]() 则可内插出状态的逼近函数y(t),由此得到y(tz)o
则可内插出状态的逼近函数y(t),由此得到y(tz)o
可以将常用的4阶定步长龙格-库塔法(RK-4)与上述连分式求零算法结合得到仿真间断系统的改进算法,并与原有算法进行比较。考虑前面提到的饱和控制系统。对改进仿真算法取步长h=0.3,RK-4方法取步长h=0.1。图2.3.3表示了两种算法的仿真误差εpk相对于初始值t0的变化。很明显,改进算法的仿真精度较原方法有很大改进。由于厄米特插值的精度阶与RK-4法的精度阶一致,因此改进算法在通过间断点时,能够保证RK-4方法的精度阶,即εpk随h4变化,而RK-4由于间断,εpk只能随h2变化。
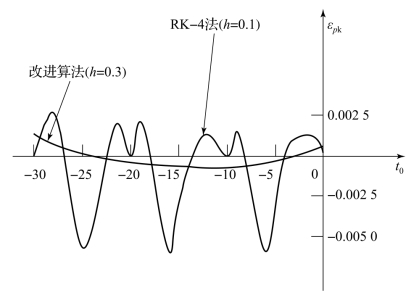
图2.3.3 RK-4法和改进算法对饱和控制系统求解的误差εpk相对于不同初始值t0的变化
连分式求零算法在间断非线性函数不多的情况下适用于实时仿真。即使在非线性函数比较多的情况下,也能在非实时仿真中提高精度。下面给出可用于非实时仿真的混合求零算法。对于φ=φ(t)的情形,它可以与任何一种变步长或定步长方法结合获得中、高精度的仿真结果。对于φ=φ(y,t)的情形,可以结合厄米特插值和4阶龙格-库塔法得到中精度的结果。
2.混合求零算法
如果条件函数在零点所在区间(t1,t2)上非单调,如φ变化很剧烈,则采用多点的连分式展开式(式2.3.6)效果往往不理想。为此,可以把三点连分式与平分法结合逐步缩小搜索区间,并逐步使用三点连分式逼近零点。图2.3.4给出了混合求零程序的框图,依据混合求零算法可以构造φ=φ(t)和φ=φ(y,t)两种情形的间断问题算法。
对于φ=φ(t)的情形,可将函数零点寻找与数值积分过程分开进行,其算法步骤如下。
(1)给定零点寻找步长hz,hz的选择应小于相邻零点的间距,另外给定积分步长hi(hi≤hz)。
(2)设由tn开始积分,令tn+1=tn+hz,判别φ(tn)φ(tn+1)是否小于0。若否,则令tn=tn+1,重复判别过程;若是,则利用混合求零程序,基于tn,tn+1求出零点tz,转步骤(3)。
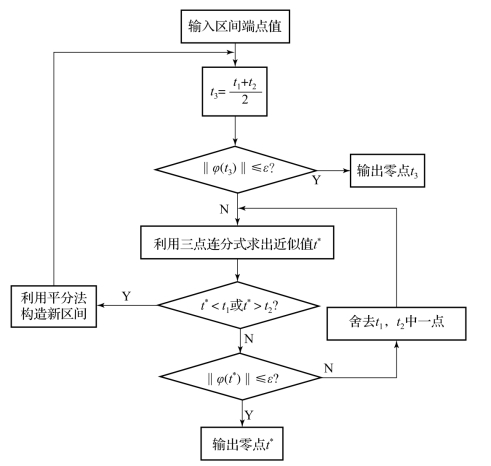
图2.3.4 混合求零程序框图
(3)基于条件函数值φ(tn),采用相应的右端函数,由开始的tn以步长hi逐步积分到tz,转步骤(4)。
(4)令tn=tz,φ(tn)=φ(tn+1),重复步骤(2)直到结束积分。
对φ=φ(y,t)的情形,算法步骤如下。
(1)选定积分步长h,由tn积分到tn+1=tn+h,判定φ(tn)φ(tn+1)是否小于0。若是,则转步骤(2);若否,则令tn=tn+1,重复步骤(1)。
(2)基于tn=tn+1,利用混合求零程序求出零点tz,其中φ(t)采用厄米特内插公式,即

式中,h=tn+1-tn;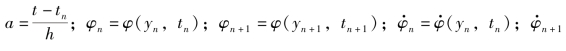 =
=![]() 。
。
(3)基于近似解yn,yn+1及其导数值![]() 同样构造厄米特公式求出修正值y(tz)。
同样构造厄米特公式求出修正值y(tz)。
(4)根据步骤(1)中得到的条件函数值φ(yn+1,tn+1)转换相应的右端函数,令tn=tz,转步骤(1)。
混合求零算法能够处理一个积分步内条件函数非单调的情况,适用于大的仿真步长和条件函数变化快的间断问题。因此,它能够仿真相当广泛的一类间断非线性系统。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




