间断非线性系统仿真算法

在控制系统和其他动力学系统的数学仿真中，还会碰到另一类特殊问题，系统的模型表示为常微分方程初值问题，但其右端函数是间断的。例如，含有间断非线性函数（符号函数、绝对值、限幅器、磁滞等）的控制系统。图2.3.1是一个饱和控制系统，它由线性饱和控制器和比例加速率反馈组成，系统的状态方程可以写为

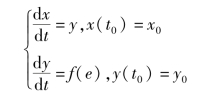
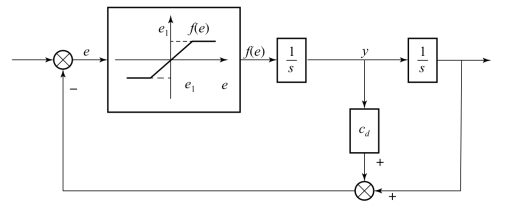
图2.3.1　饱和控制系统

式中，e＝－x－cd y，而右端函数则呈间断形式，即

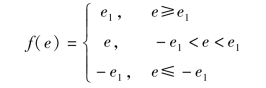(www.xing528.com)

若令φ1＝e－e1，φ2＝e＋e1，则f（e）可以改写为

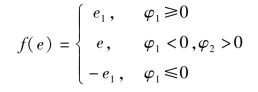
间断非线性系统的数学模型可以表示为下面的一般形式：

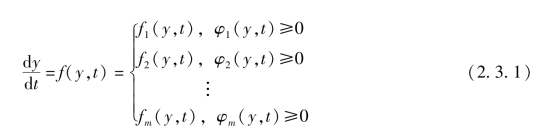
式中，微分方程的右端函数有m个不同的状态，采取何种状态则要由条件函数φ决定。如果条件函数只依赖于时间t，则可以通过求函数零点的方法，预先求出间断点，在积分到间断点附近时改变步长积分到间断点，然后转换相应右函数，重新进行仿真计算。在一般情况下，条件函数φ与状态变量y亦有关。因此，在仿真过程中无法预先知道φ的零点。这样，如果用通常的定步长数值积分法进行仿真，由于间断点往往出现在积分步中间，因此在跨越间断点时对右函数进行赋值会产生很大的误差。如果采用变步长方法，则要在间断点附近不断缩小步长来满足精度要求，从而出现振荡现象，使仿真的时间和工作量都大大增加。而且，对于间断严重的问题，即使步长变得很小仍然不能满足精度要求。

解决这类问题一般可采取3种办法：①应用求平均值的思想，把间断点对积分的影响考虑到仿真算法中；②在仿真算法中附加一个零点搜索程序，遇到有间断点的情况，由其求出间断点，然后从间断点继续积分；③改进一般的数值积分算法，使其在积分过程中同时估计出间断点的位置。上述3种方法各有其优缺点。可以根据系统的模型和仿真的要求加以选择。方法③可以应用到写不出条件函数的情况，但目前尚无非常有效的算法。