离散相似法在结构图上的应用

面向结构图仿真方法的基本思想就是将结构图化简为各个典型环节，然后在各个典型环节前加入虚拟的采样器和保持器使各环节独自构成一个便于计算机仿真的差分方程。下面首先求出各种典型环节的离散状态方程。

1.积分环节

如图2.2.8所示，传递函数为

状态表达式为

对比式（1.3.39），可知A＝0，B＝K，所以

可得离散状态表达式

2.比例－积分环节

如图2.2.9所示，传递函数为

状态表达式为

类似地，可得离散状态表达式

图2.2.8　积分环节

图2.2.9　比例－积分环节

3.惯性环节

如图2.2.10所示，传递函数为

状态表达式为

则Φ（T）＝e－aT，，可得离散状态表达式

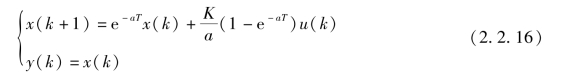
4.比例－惯性环节

如图2.2.11所示，传递函数为

状态表达式为

(www.xing528.com)

则Φ（T）＝e－aT，，可得离散状态表达式

图2.2.10　惯性环节

图2.2.11　比例－惯性环节

5.2阶振荡环节

如图2.2.12所示，传递函数为

图2.2.12　2阶振荡环节

状态表示式为

则计算

式中，，可得离散状态表示式

式中，X＝［x1x2］T，C＝［dc］。

为了实现面向结构图模型的离散相似法仿真，需要建立系统的连接矩阵，以保证正确的计算次序。

设系统的第i个环节的输入、输出分别用ui、yi（i＝1，2，…，n）表示，y0为系统的外部输入量，则

可把式（2.2.22）改写成

式中，W是一个n×（n＋1）维长方矩阵。这是把表示输入信号与系统连接情况的W0矩阵

放在原连接矩阵的第一列，也就是W＝，Wij表示第j个环节输出与第i个环节输入之间的连接方式。Y是一个（n＋1）×1维的列向量，Y＝［y0y1y2…yn］T。

例如，有一系统如图2.2.13所示，如果已知各环节的传递函数，则很容易将其离散化，而各环节的输入输出关系为

图2.2.13　系统结构图

面向系统结构图离散化仿真的工作流程如图2.2.14所示。

图2.2.14　面向系统结构图离散化仿真的工作流程

面向结构图仿真需按环节离散化，这相当于在每个环节的入口处都加了一个虚拟的采样器及零阶保持器，从控制理论上讲这些采样器及保持器都要引进滞后；从数值计算方法上讲会带来误差。所以，环节越多，所引进的误差也将越大，这时就需要减小计算步长（采样周期）。对于时不变系统，状态转移矩阵是常数矩阵，它只需计算一次，占用计算机的时间不多。而状态变量和输出变量的计算，是按环节依次进行的，每计算一个动态响应点，各环节都需计算一次，故计算机的工作时间几乎随环节的减少成比例减少。按环节离散化的优点是整个运算程序段计算量较小，可提高仿真速度；另外，便于引入非线性环节，适用于非线性系统仿真。