离散相似模型的精度和校正问题-车辆系统仿真理论与实践中的结果

离散相似模型的精度是指离散相似模型与原连续系统模型等效（近似）的程度。连续系统的离散化过程中加入了虚拟的采样开关和保持器，由于保持器不可能完整无误地将连续信号重构出来，因此离散相似模型必然存在误差。这种误差与虚拟采样开关的采样周期T及所用保持器有关。一般来讲，采样周期越大，仿真的误差也就越大。采样频率首先必须满足采样定理，即

fs≥2fm

式中　fs——采样频率；

fm——连续信号的最大频率。

在此基础上，从保障系统稳定性、仿真精度及仿真速度等方面综合考虑选择T。实际应用时，采样周期T可按最大频率的30～50倍选择，即

选择了合适的采样周期，还需要一个理想的信号保持器，重构连续信号。常用的保持器有零阶保持器、一阶保持器和三角形保持器。其中，零阶保持器能无失真地复现阶跃输入，且结构简单，易于实现，但具有相位滞后特性，对仿真模型的稳定性有一定的影响；一阶保持器虽然能较好地复现斜坡输入，但也有相位滞后特性；三角形保持器既有较好的低通滤波特性，又无相位滞后特性，其特性最好，但不容易实现。若采样频率足够高，又采用了较合适的保持器，信号的失真就会很小，也就能保证离散相似模型具有较高的精度。

另一方面，为了减少误差，可以加入校正补偿环节对离散相似模型进行校正。一般所加入的补偿器应尽可能好地抵消经过采样－保持器所造成的失真，补偿器常常采用超前的λeγsT的形式，其中λ，γ可以根据实际情况选取。

仍然以积分环节为例来说明这种方法的基本原理，整个仿真模型如图2.2.6所示。

图2.2.6　加校正的数字仿真模型

按图2.2.6所构成的仿真模型的G（z）为

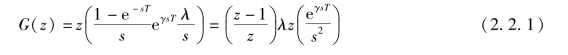
对λeγsT做一次近似，即

则式（2.2.1）变成(www.xing528.com)

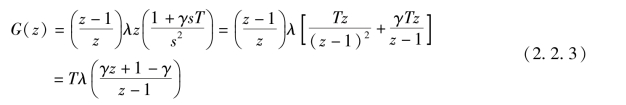
写成差分方程为

选择不同的γ和λ，可得各种不同的数值积分公式。例如：

选λ＝1，γ＝0，则有yn＝yn－1＋Tun－1（欧拉公式）。

选（梯形公式）。

选λ＝1，γ＝1，则有yn＝yn－1＋Tun（超前欧拉公式）。

梯形公式及超前欧拉公式都有yn项，一般它是未知的，在计算yn时只知道yn－1。为此，可以先对输入信号加一拍延滞，然后再加大γ，补偿这种延滞所造成的误差。如图2.2.7所示，则有

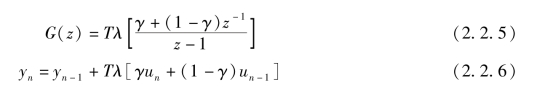
图2.2.7　补偿延滞造成的误差

选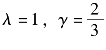，根据式（2.2.6）可得

这就是亚当姆斯公式。

由于λ，γ可调，故将式（2.2.4）及式（2.2.6）称为可调整的数值积分公式。把这种方法用于复杂系统的快速仿真，就可以得出允许较大步长、又有一定精度的仿真模型。通常将这种方法称为可调的数值积分法。

利用上述步骤仅仅是计算出了系统的输入量y。如果还关心系统中的其他状态变量，那么就必须将系统分成几个部分，每部分都要加虚拟的采样器及保持器。再按一般系统的校正原则，对每一个小闭环加一个λeγsT进行校正。调整时，一般是先调整外环，再调整内环，使所获得的仿真模型在较大的计算步长时仍能最好地与实际模型相接近。λ，γ可采用参数寻优的办法来确定。