算法误差和稳定性问题的解决方法

算法误差主要包括两种误差：截断误差和舍入误差。

1.截断误差

基于泰勒展开公式的数值计算方法都存在截断误差，假定前一步得到的结果yn是准确的，则用泰勒级数求得tn＋1处的精确解为

若只从以上精确解中取前两项之和来近似计算yn＋1，由这种方法单独一步引进的附加误差通常称作局部截断误差，它是由该方法给出的值与微分方程的解之间的差，故又称为局部离散误差。不同的数值解法，其局部截断误差也不同。一般，若差分公式局部截断误差为o（hr＋1），则称它有r阶精度，即方法是r阶的，所以方法的阶数可以作为衡量算法精确度的一个重要标志。

截断误差的阶次越高，其求解的精度越高。前面介绍的积分方法的截断误差分别为

欧拉法　　　　　εt＝o（h2）

梯形法　　εt＝o（h3）

4阶龙格－库塔法εt＝o（h3）

亚当姆斯法　　εt＝o（h3）

2.舍入误差

由于积分算法是由有限精度（字长）的计算机算术运算来实现的，因此必定要引入舍入误差。舍入误差会积累，它随着积分时间的增加和积分法阶次的增高而增加，并且它还随着积分步长的减小而变得愈加严重。这是因为对于给定的积分时间，使用更小的步长就意味着更多的积分步数。

3.稳定性问题

稳定性是数值积分法中非常重要的概念。所谓稳定性问题是指误差的积累是否受到控制的问题。如果在每步计算过程中，前面积累的舍入误差对实际误差εr（εr＝计算值－实际值）的影响是减弱的，则计算方法是稳定的；反之，则可能由于εr的恶性增长而变得不稳定。如果计算过程发生不稳定情况，则计算结果将失去意义，而且可能导致人们作出错误的判断。

通常，把数值积分法用于试验方程

来判断积分算法的稳定性。若数值积分公式为

则当差分方程满足稳定条件＜1时，算法才稳定。

下面对几种数值积分法进行稳定性分析。

1）欧拉法

把欧拉公式yn＋1＝yn＋hfn应用到上述试验方程，得到

对式（2.1.28）进行Z变换后得

此差分方程的特征方程为

z－（1＋λh）＝0(www.xing528.com)

根据差分方程稳定条件得

式（2.1.30）称为欧拉公式的稳定性条件，它对λh的限制构成了复平面上以（－1，0）为圆心的单位圆（见图2.1.6），也称为欧拉公式的稳定区域。如果积分步长取得足够小使λh落在稳定区域内，则欧拉公式是稳定的。

2）梯形法

梯形积分公式为

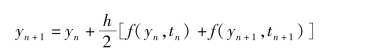
代入试验方程，取Z变换后得

其特征根为

即

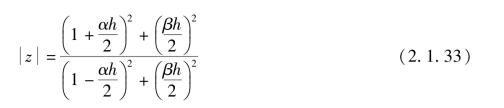
可见，若α＜0，则　，故梯形积分公式也为恒稳公式。

以同样的方法对其他积分方法的稳定性进行分析，图2.1.7、图2.1.8描述了龙格－库塔法和亚当姆斯法的稳定区域（注意：稳定域关于实轴对称，图2.1.7、图2.1.8只画了上半部分）。

图2.1.6　欧拉公式的稳定区域

图2.1.7　1～4阶龙格－库塔法的稳定区域（区域内部）

图2.1.8　常用的1～4阶亚当姆斯法的稳定区域

（a）显式；（b）隐式

可见，区域内部，其中1阶、2阶隐式方法是恒稳的。

（1）对龙格－库塔法，阶次k增大则稳定区域略微增大。

（2）对亚当姆斯法，阶次k增大则稳定区域反而缩小。

另外，常用数值积分法中，欧拉法，梯形法，隐式1阶、2阶亚当姆斯法为恒稳法，其余是条件稳定的。

4.步长的选择

从数值计算观点看，步长越小，截断误差越小；但是步长减小将导致步数的增多，舍入误差积累就会增加，如图2.1.9所示。因此，要兼顾截断误差和舍入误差两个方面选取合理的步长。从控制理论观点来看，步长的选择与控制系统的频带及构成仿真系统环节数的多少等因素有关，要根据仿真精度给出一个计算步长的解析公式是很困难的。在实际工作中，通常根据被仿真系统的响应速度由经验确定。一般要求步长小于系统的时间常数的1／10。若系统变量的变化频率为f0，则与步长T相对应的间隔频率f1应为f0的20～100倍。