常用数值积分法及车辆系统仿真

1.欧拉法

欧拉法是最简单的一种数值积分法，虽然它的计算精度较低，实际中很少被采用，但其推导简单，能说明构造数值解法一般计算公式的基本思想。

对式（2.1.1）两端由t0到t1进行积分，得到

式（2.1.3）中的积分项是曲线f及t＝t0，t＝t1包围的面积（如图2.1.1所示），当步长h＝tn－tn－1足够小时，可以用矩形面积来近似表示，即

令y（t1）的近似值为y1，则有

把t1当作积分初始点，y1作为初始值重复上述做法，可进一步得到y（t2）的近似公式，继续重复可得到递推公式

式（2.1.6）称为欧拉公式，也称为矩形法。由式（2.1.6）可以看出，任何一个新的数值解yn＋1都是基于前一个数值解yn以及它的导数f（yn，tn）求得的。若已知初值y0，利用式（2.1.6）进行迭代计算，即可以求得式（2.1.1）在t＝t1，t2，…，tn处的近似解y（t1），y（t2），…，y（tn）。

欧拉法的几何意义十分清楚。图2.1.2通过（t0，y0）点作积分曲线的切线，其斜率为f（y0，t0），此切线与t1处平行于y轴直线的交点即为y1，再过（t1，y1）点作积分曲线的切线，它与过t2平行于y轴直线的交点为y2。这样过（t0，y0），（t1，y1），（t2，y2），…得到一条折线，称为欧拉折线。

图2.1.1　矩形近似及其误差

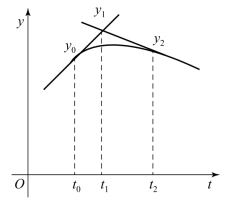
图2.1.2　欧拉折线

2.梯形法

在上面的推导中，若用梯形面积（见图2.1.3）来近似表示式（2.1.3）中的积分项，则可得到梯形公式：

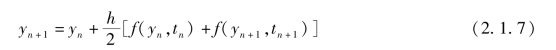
由式（2.1.7）可见，它是隐函数形式。公式右端隐含有待求量yn＋1，故梯形法不能自启动。通常可用欧拉法启动求出初值，算出y（tn＋1）的近似值，然后将其代入原微分方程，计算fn＋1的近似值，最后利用梯形公式求出修正后的yn＋1。为了提高计算精度，可用梯形公式反复迭代。通常在工程问题中，为简化计算，只迭代一次，这样可得改进的欧拉公式为

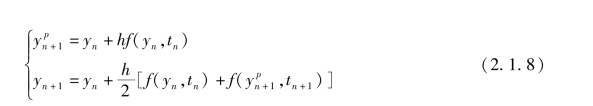
式（2.1.8）中，第一式称为预估公式，第二式称为校正公式。通常称这类方法为预估－校正法，也称为改进欧拉法。欧拉法每计算一步只要对导数f调用一次，改进的欧拉法由于加了校正过程，计算量增加了一倍，付出这种代价的目的是提高精度。预估－校正法程序框图如图2.1.4所示。

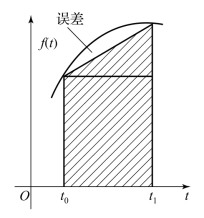
图2.1.3　梯形近似及其误差

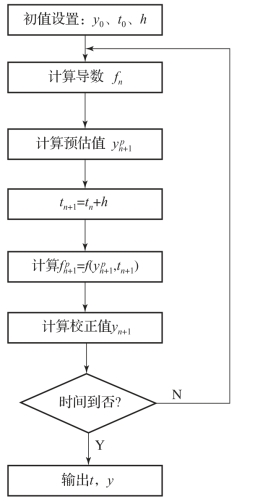
图2.1.4　预估－校正法程序框图

3.龙格－库塔法

将式（2.1.1）在tn点展开成泰勒级数：

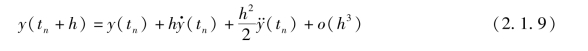
取泰勒展开式的前两项可以得到欧拉公式，其误差较大，如果要得到精度更高的近似解，必须计算式中的高阶导数，这项工作往往相当困难。德国数学家C.Runge和M.W.Kutta两人先后提出了间接利用泰勒展开式的方法，即用几个点上的函数f值的线性组合来确定其中的系数。基于这一思想，得到龙格－库塔法的一般形式为

式中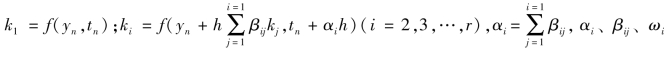，为待定系数，r为使用k值的个数（即阶数）。

在给定r值后，通过把式（2.1.10）展开成h的幂级数，然后和泰勒展开式的系数进行对比，以确定βij，ωi的值。

当r＝1时，得到的数值解即为欧拉公式(www.xing528.com)

yn＋1＝yn＋hf（yn，tn）

当r＝2时，取，继而可得到

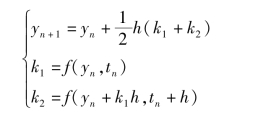
与式（2.1.8）相比，二者完全相同，所以预估－校正公式实际上是2阶龙格－库塔公式。当阶次大于4阶后，龙格－库塔公式右端函数的计算次数要大于阶数，使积分工作量大大增加，所以通常只使用4阶或4阶以下的方法。表2.1.1给出了常用的1～4阶龙格－库塔方法的系数。

表2.1.1　常用的1～4阶龙格－库塔方法的系数

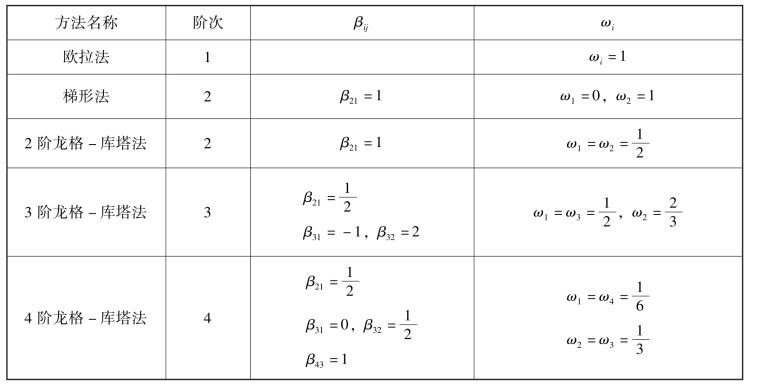
4阶龙格－库塔法是使用较多的一种方法，其公式为

龙格－库塔法属于单步法，只要给定方程的初值y0就可以一步步求出y1，y2，…，yn的值。故单步法有下列优点：①需要存储的数据量少，占用的存储空间少；②只需要知道初值，即可启动递推公式进行运算，可自启动；③容易实现变步长运算。

4.亚当姆斯法

亚当姆斯法是线性多步法。在利用多步法计算yn＋1值时，必须已知除yn＋1外前几步的值，如yn，yn－1，…，yn－k＋1，称为k步法。线性多步法不能自启动，需先用其他方法求出y1，y2，…，yk－1的值才能用多步法求解。线性多步法的递推计算公式可写为

式中，fn－i＝f（yn－i，tn－i），αi、βi为待定系数。如果β－1＝0，则式（2.1.12）的右端不含有yn＋1，公式为显式；如果β－1≠0，则式（2.1.12）的右端含有yn＋1，公式为隐式。

亚当姆斯法是利用一个插值多项式来近似代替f（y，t）。在tn－k＋1到tn区间内等间距取k个点tn－k＋1，tn－k＋2，…，tn，并算出它们的右端函数值fn－k＋1，fn－k＋2，…，fn，然后由这k个值根据牛顿后插公式进行插值，得到一个k－1次多项式逼近f（y，t），即

f（y，t）≈fn Pn（t）＋fn－1 Pn－1（t）＋…＋fn－k＋1 Pn－k＋1（t）

这里Pn－j（t）是插值的基函数，即在节点tn－j取1，在其他节点取值为0。其实质是在外插区间［tn，tn＋1］上积分，如图2.1.5所示。

图2.1.5　线性多步格式

由此可得到亚当姆斯法显式公式（简称显式AB法公式）

若用牛顿内插公式，则

f（y，t）≈fn＋1 Pn＋1（t）＋fn Pn（t）＋…＋fn－k＋2 Pn－k＋2（t）

Pn＋1－j（t）是在节点tn＋1－j取1，在其他节点取0的多项式。则可求得亚当姆斯法隐式公式（简称隐式AB法公式）

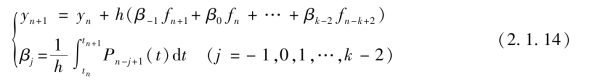
表2.1.2列出了常用亚当姆斯法的系数。

表2.1.2　常用亚当姆斯法的系数

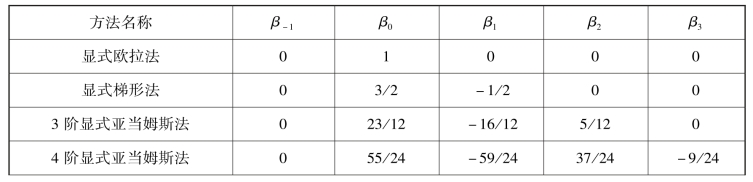
续表

常用的4阶亚当姆斯法显式公式为

由于隐式公式的稳定域大于显式公式的稳定域，而且对同阶的亚当姆斯法来说，隐式公式的精度往往要高于显式公式，因此采用折中的办法，先由显式公式求出yn＋1的预估值，再代入隐式公式求出yn＋1的值。这种方法为预估－校正法，4阶预估－校正公式为