车辆系统仿真：计算机控制系统的数学模型

在对连续系统离散化时，人为地加入了采样开关和保持器，而在计算机控制系统中实际就存在采样开关和保持器，它由离散部分（数字计算机或数字控制器）和连续部分（保持器或数／模转换器以及控制对象）组成，如图1.3.9所示。

图1.3.9　计算机控制系统

设数字控制器的运算关系为1，即u（kT）＝e（kT），则图1.3.9中的1，2两部分可合并，如图1.3.10所示。

假定保持器为零阶，即u（t）是e（kT）的阶梯状分段连续函数，则有

对上式取拉普拉斯变换，可得

令

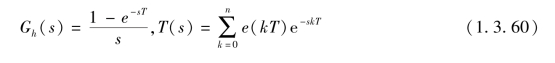
则有

可以证明

(www.xing528.com)

在一般情况下

因此，可以设想e*（t）是由图1.3.11所示的虚拟系统产生的脉冲序列。图中的开关每隔T闭合一次，以产生脉冲序列。同理，Gh（s）用以定义将e*（t）这样的脉冲序列变成阶梯形的环节。综上所述，图1.3.12（a）和图1.3.12（b）所示的两个系统是等价的。

图1.3.10　采样开关和保持器

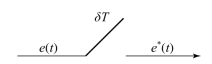
图1.3.11　产生脉冲序列的虚拟系统

因此，图1.3.9所示的计算机控制系统的数学模型可表示成图1.3.13所示的模型，其中D（z）为数字控制器的z传递函数，Gh（s）为保持器的传递函数，G（s）为连续控制对象的传递函数。

图1.3.12　零阶保持器及其传递函数

图1.3.13　计算机控制系统的数学模型

计算机控制系统的模型与连续系统离散化模型形式相同，都是差分方程，所以从仿真方法来讲两者都是相同的。但是，连续系统离散化模型是一种近似模型，因为在建立模型的过程中人为地加入了采样开关和保持器，所以它只能是近似描述原来的连续系统；而计算机控制系统仿真的特点是，数字控制器是实际存在的离散量运算，采样开关也是实际存在的。